整数规划基本原理
1.1 定义
规划中的变量(部分或全部)限制为整数时,称为整数规划。若在线性规划模型中,变量限制为整数,则称为整数线性规划。目前所流行的求解整数规划的方法,往往只适用于整数线性规划。目前还没有一种方法能有效地求解一切整数规划。

整数规划问题的特点在于其决策变量含有整数变量


摘自于【整数规划(一)】整数规划问题综述 (zhihu.com)
:
一般来说,之所以在模型中要引入整数变量主要原因有2点:
1 我们所需要描述的变量来自生活实际,而这些变量都是整数的。例如:要表示 多少架飞机,多少辆汽车,多少个人 等等 这些变量必然只能是整数的,这些实际问题中的变量若取分数则失去了实际意义,因此我们必须用整数变量来进行建模。
2 我们要描述逻辑,Yes 或者 No,乃至于更复杂的逻辑关系。我们经常会用1代表Yes,0代表No,从这里也可以衍生出很多复杂的逻辑关系。值得注意的是区别于前一种情况此时的整数变量看起来貌似还是整数的形式,但实际上准确的来说说 它们已经是 Bool 变量了。Bool 变量满足 Bool 变量的运算法则,例如 与或非这些,而不满足加减乘除的运算规则。明白了这一点对整数规划问题的建模有着很大的帮助。
分类:


求解方法
分支定界算法求解整数线性规划问题
第一个是穷举法,浪费时间空间
分支定界法:先求出相应松弛问题的最优解
若松弛问题无可行解,则 ILP 无可行解
若松弛问题最优解符合整数要求,则是最优解
若不满足整数条件,则任选一个不满足整数条件的变量x来构造心得约数添加到松弛问题形成两个子问题,依次在减小的可行域求解新的最优解,并重复,直到子问题无解,或整数有最优解。
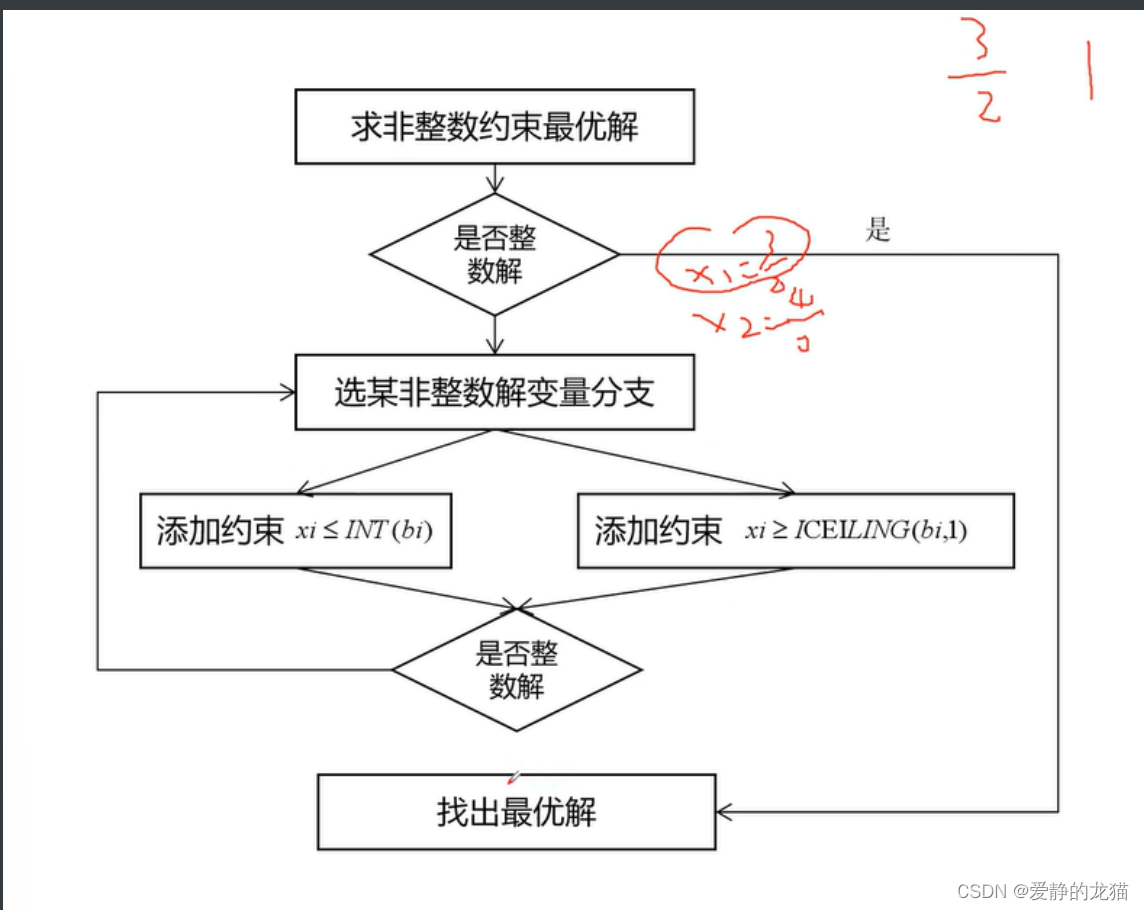
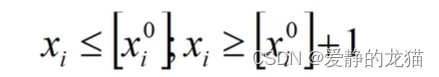
再谈分支定界,增强理解

上界缩小,下界增大,直到求出为止。
步骤一:确定初始定界,求解线性规划B的最优解,作为初始上界,求解A的一个整数解,作为初始下界。
步骤二:选择B最优解不满足整数条件的变量,约束B为两个子问题,求出B1,B2的最优解
步骤三:比较各分支的解,将最优目标函数值的最大值作为下界,将各分支整数条件的最大值作为新的下界。
步骤四:剪枝,比较各分支的解,若小于新的下界,则剪枝,若无可行解,剪枝,若大于新的下界,那么重复2,3,4.
按照以上步骤不断更新即可。
割平面法的基本思想


割掉的部分只包含非整数解。
步骤一:将约束条件中的系数和常熟化为整数,然后采用单纯形法求解不考虑整数约束的线性规划问题的最优解。
步骤二:在最终单形法中选择一个非整数基变量所在的约束等式,将该约束等式的系数和常熟分解为整数和非真分数之和。
步骤三:将所有整数部分放在左边,分数放在右边,根据各变量的约束特点分析等式右边,得到切割方程。
步骤四:将切割方程代入线性规划问题的最终表中求解最优解,若仍然未得到最优整数解,重述步骤二到步骤四。


0-1规划


常用约束条件的表达方式

隐枚举法
求解思路及改进措施:
(1) 先试探性求一个可行解,易看出(x1, x2 , x3 ) = (1,0,0) 满足约束条件,故为一个可行解,且 z = 3。
(2) 因为是求极大值问题,故求最优解时,凡是目标值 z < 3的解不必检验是否满足约束条件即可删除,因它肯定不是最优解,于是应增加一个约束条件(目标值下界):
(3) 改进过滤条件。
(4)由于对每个组合首先计算目标值以验证过滤条件,故应优先计算目标值 z 大的组合,这样可提前抬高过滤门槛,以减少计算量。
指派问题--匈牙利算法
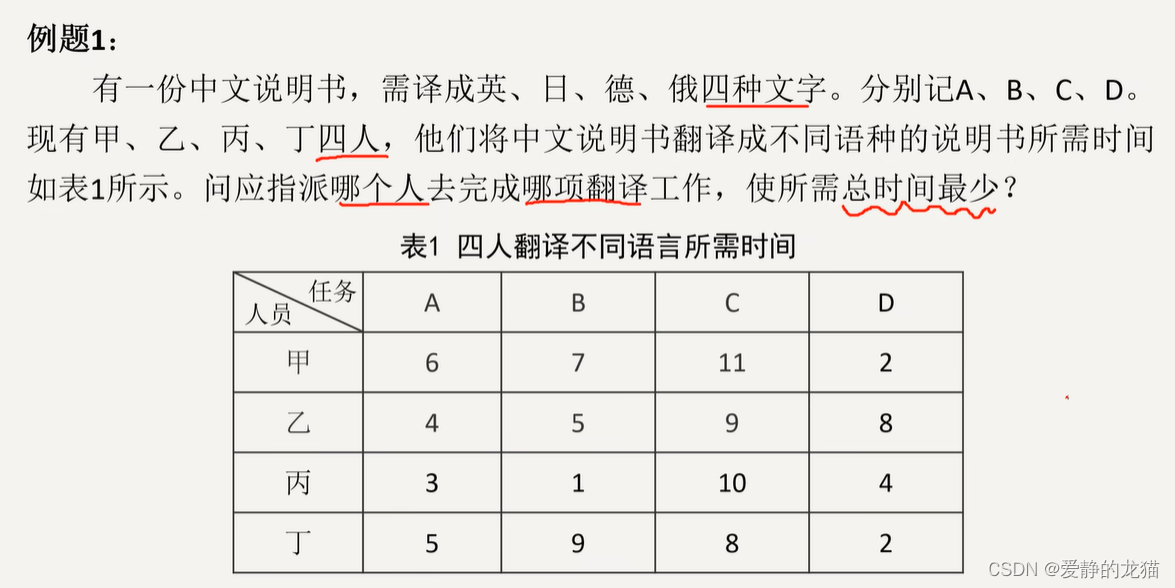

指派问题模型引入

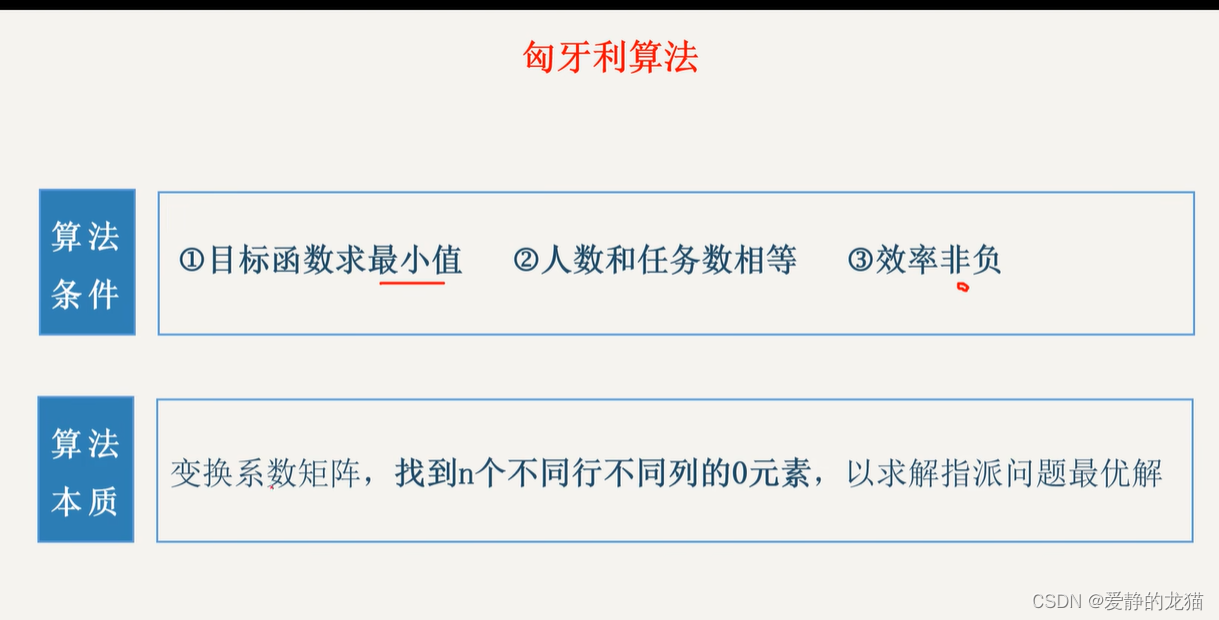
匈牙利算法步骤:
步骤一:系数矩阵初等行变换,再进行初等列变换,使得各行各列出现0元素。
注意,减去的是最小值。
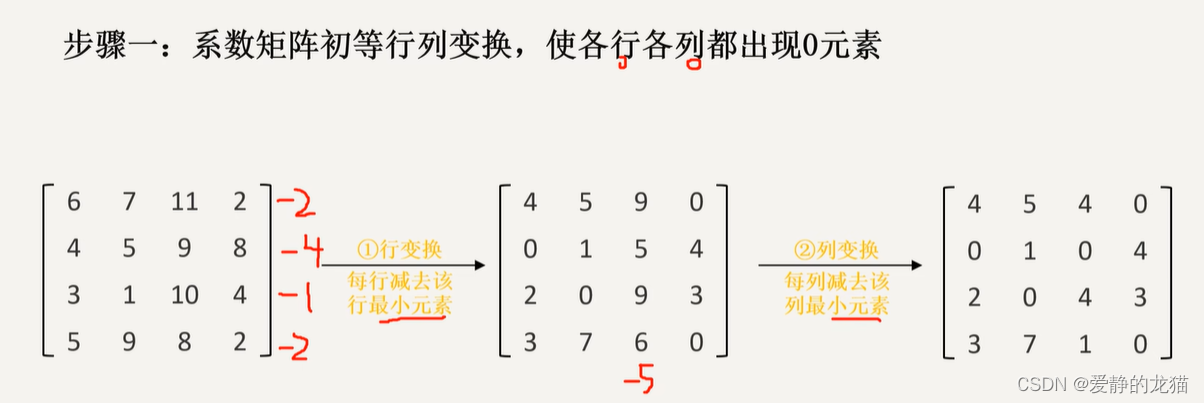
步骤二:找到只有一个0元素的行,花圈,划去该列其他0元素
同理,再对列做这件事清

步骤三:
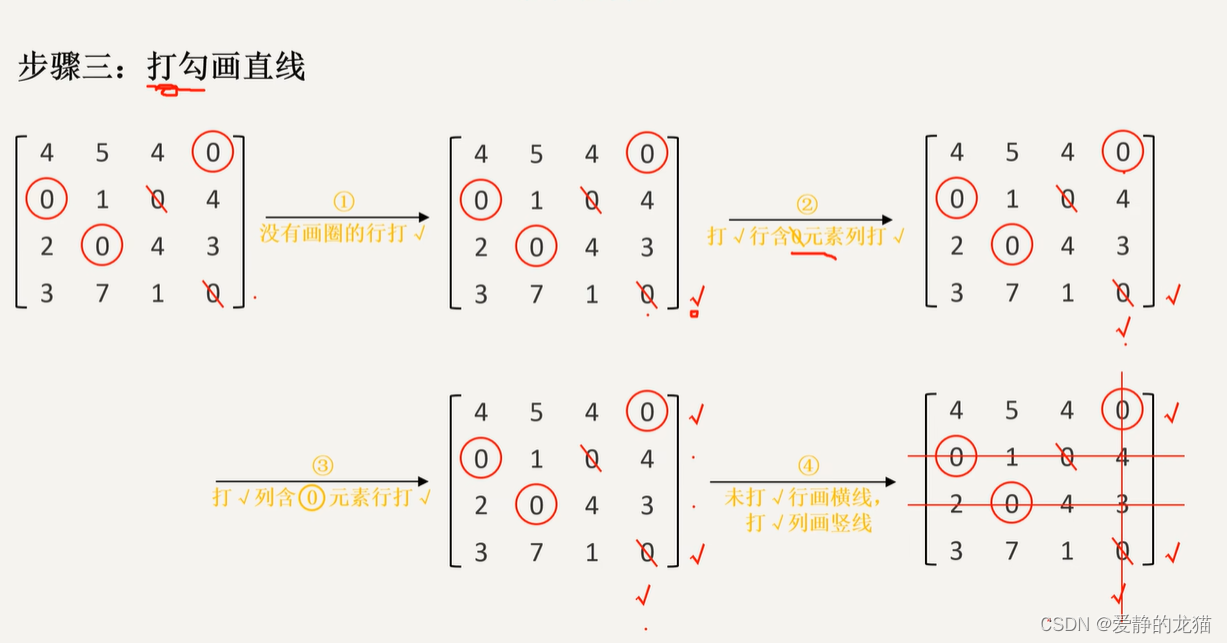
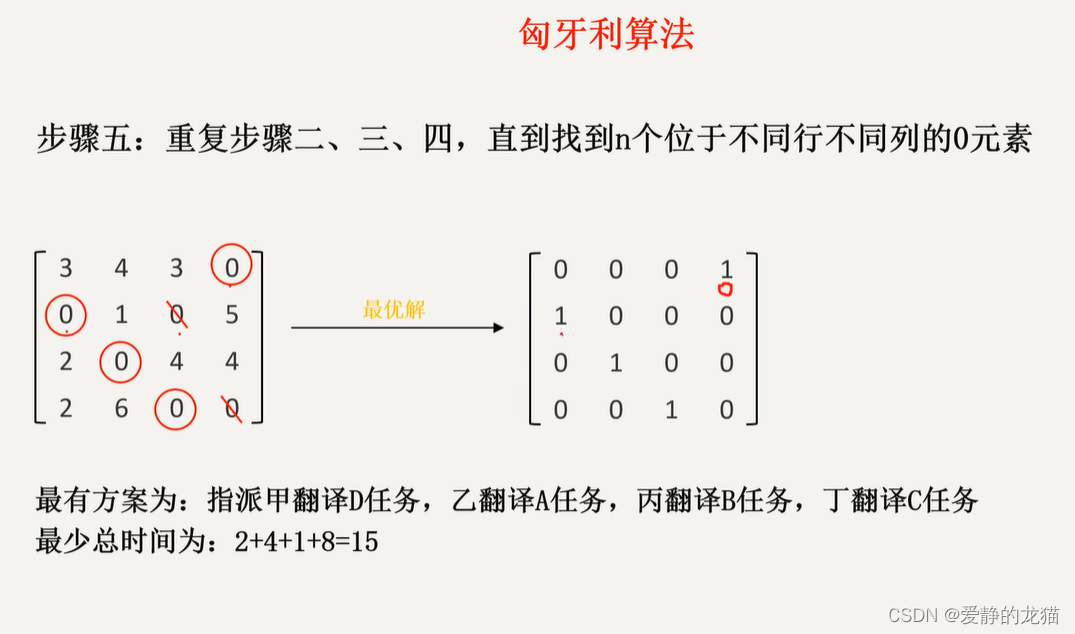
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- SEO优化三个小窍门
- 消费者痛点怎么分析,不同行业如何营销
- 【电商项目实战】购物车完善
- electron 弹出软键盘 / 执行c#代码
- 富文本编辑器wangEdtor的使用,vue2引入wangEdtor
- 2023年度总结(找到工作)
- 数据库的内连接和外连接的区别
- 【洛谷 P2084】进制转换 题解(模拟+字符串)
- 【微服务】日志搜集es+kibana+filebeat+redis+logstash(单机)
- burp靶场--操作系统命令注入