微分和导数(一)
发布时间:2023年12月18日
1.微分:
假设我们有?个函数f : R → R,其输?和输出都是标量。如果f的导数存在,这个极限被定义为
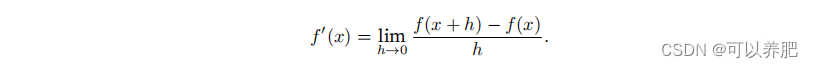
如果f′(a)存在,则称f在a处是可微的。如果f在?个区间内的每个数上都是可微的,则此函数在此区间中是可微的。导数f′(x)解释为f(x)相对于x的瞬时变化率。所谓的瞬时变化率是基于x中的变化h,且h接近0。
给定y = f(x),其中x和y分别是函数f的?变量和因变量。以下表达式是等价的:

2.偏导数:
设y = f(x1, x2, . . . , xn)是?个具有n个变量的函数。y关于第i个参数xi的偏导数为:

对于偏导数的表?,以下是等价的:

3.导数和微分的理解:
导数是描述函数变化的快慢,微分是描述函数变化的程度。
导数是比值,微分是增量。
导数是函数的局部性质,一个函数在某一点的导数描述了这个函数在这一点附近的变化率。微分是一个函数表达式,用于自变量产生微小变化时计算因变量的近似值。
导数是针对一个自变量的,微分是针对所有自变量的,多元函数的导数是指多元函数的偏导数,它是指在多元函数中,每个变量的偏导数的集合。
导数的几何意义是该函数曲线在这一点上的切线斜率。
微分的几何意义是用局部切线段近似代替曲线段,即非线性函数局部线性化。
4.梯度:
梯度是?个向量,其分量是多变量函数相对于其所有变量的偏导数。
设函数f : Rn → R的输?是?个n维向量x = [x1, x2, . . . , xn]?,并且输出是?个标量。函数f(x)相对于x的梯度是?个包含n个偏导数的向量:

5.链式法则:
在深度学习中,多元函数通常是复合(composite)的,所以微分这些函数比较难,链式法则可以被?来微分复合函数。
假设函数y = f(u)和u = g(x)都是可微的,根据链式法则:
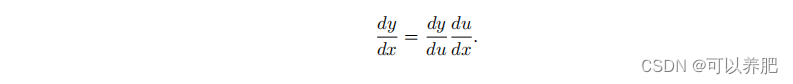
假设可微分函数y有变量u1, u2, . . . , um,其中每个可微分函数ui都有变量x1, x2, . . . , xn,根据链式法则:
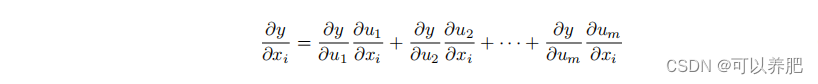
文章来源:https://blog.csdn.net/qq_39879126/article/details/135041751
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章