K - 近邻算法
1、算法介绍
KNN(K Near Neighbor):k个最近的邻居,即每个样本都可以用它最接近的k个邻居来代表。KNN算法属于监督学习方式的分类算法,我的理解就是计算某给点到每个点的距离作为相似度的反馈。
简单来讲,KNN就是“近朱者赤,近墨者黑”的一种分类算法。
KNN是一种基于实例的学习,属于懒惰学习,即没有显式学习过程。
要区分一下聚类(如Kmeans等),KNN是监督学习分类,而Kmeans是无监督学习的聚类,聚类将无标签的数据分成不同的簇。
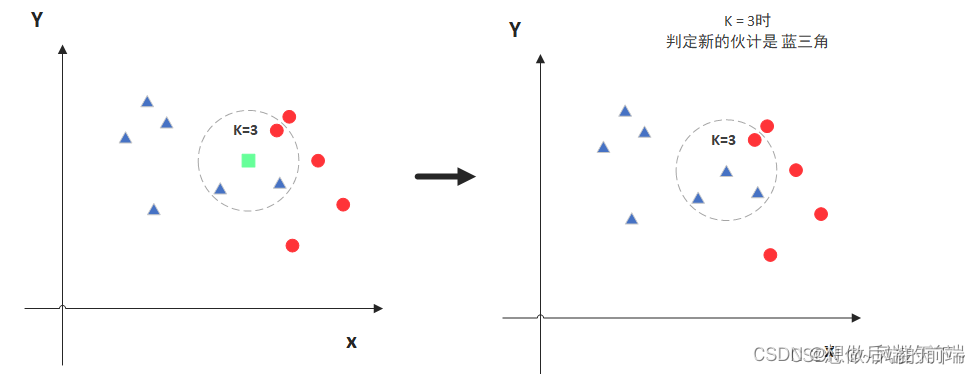 图中绿色的点就是我们要预测的那个点,假设K=3。那么KNN算法就会找到与它距离最近的三个点(这里用圆圈把它圈起来了),看看哪种类别多一些,比如这个例子中是蓝色三角形多一些,新来的绿色点就归类到蓝三角了。
图中绿色的点就是我们要预测的那个点,假设K=3。那么KNN算法就会找到与它距离最近的三个点(这里用圆圈把它圈起来了),看看哪种类别多一些,比如这个例子中是蓝色三角形多一些,新来的绿色点就归类到蓝三角了。
 但是,当K=5的时候,判定就变成不一样了。这次变成红圆多一些,所以新来的绿点被归类成红圆。从这个例子中,我们就能看得出K的取值是很重要的。
但是,当K=5的时候,判定就变成不一样了。这次变成红圆多一些,所以新来的绿点被归类成红圆。从这个例子中,我们就能看得出K的取值是很重要的。
明白了大概原理后,我们就来说一说细节的东西吧,主要有两个,K值的选取和点距离的计算。
2、距离计算
要度量空间中点距离的话,有好几种度量方式,比如常见的曼哈顿距离计算,欧式距离计算等等。不过通常KNN算法中使用的是欧式距离,这里只是简单说一下,拿二维平面为例,二维空间两个点的欧式距离公式如下:

三维空间两个点的欧式距离为:
拓展到多维空间后的距离公式为:
3、K值的选取
通过上面那张图我们知道K的取值比较重要,那么该如何确定K取多少值好呢?答案是通过交叉验证(将样本数据按照一定比例,拆分出训练用的数据和验证用的数据,比如6:4拆分出部分训练数据和验证数据),从选取一个较小的K值开始,不断增加K的值,然后计算验证集合的方差,最终找到一个比较合适的K值。
?
通过交叉验证计算方差后你大致会得到下面这样的图:

这个图其实很好理解,当你增大k的时候,一般错误率会先降低,因为有周围更多的样本可以借鉴了,分类效果会变好。但注意,和K-means不一样,当K值更大的时候,错误率会更高。这也很好理解,比如说你一共就35个样本,当你K增大到30的时候,KNN基本上就没意义了。
所以选择K点的时候可以选择一个较大的临界K点,当它继续增大或减小的时候,错误率都会上升,比如图中的K=10。
参考李航博士一书统计学习方法中写道的K值选择:
- K值小,相当于用较小的领域中的训练实例进行预测,只要与输入实例相近的实例才会对预测结果,模型变得复杂,只要改变一点点就可能导致分类结果出错,泛化性不佳。(学习近似误差小,但是估计误差增大,过拟合)
- K值大,相当于用较大的领域中的训练实例进行预测,与输入实例较远的实例也会对预测结果产生影响,模型变得简单,可能预测出错。(学习近似误差大,但是估计误差小,欠拟合)
- 极端情况:K=0,没有可以类比的邻居;K=N,模型太简单,输出的分类就是所有类中数量最多的,距离都没有产生作用。
?
4、算法实现
4.1?Scikit-learn工具介绍

- Python语言的机器学习工具
- Scikit-learn包括许多知名的机器学习算法的实现
- Scikit-learn文档完善,容易上手,具有丰富的API
- 目前稳定版本为0.19.1
安装:
pip3 install scikit-learn==0.19.1?4.2?基本流程描述
- 计算当前点与所有点之间的距离
- 距离按照升序排列
- 选取距离最近的K个点
- 统计这K个点所在类别出现的频率
- 这K个点中出现频率最高的类别作为预测的分类
4.3用sklearn中的KFold进行K折交叉验证
import numpy as np
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import KFold #主要用于K折交叉验证
# 导入iris数据集
iris=datasets.load_iris()
X=iris.data
y=iris.target
print(X.shape,y.shape)
# 定义我们想要搜索的K值(候选集),这里定义8个不同的值
ks=[1,3,5,7,9,11,13,15]
# 例:进行5折交叉验证,KFold返回的是每一折中训练数据和验证数据的index
# 假设数据样本为:[1,3,5,6,11,12,43,12,44,2],总共10个样本
# 则返回的kf的格式为(前面的是训练数据,后面的是验证数据):
# [0,1,3,5,6,7,8,9],[2,4]
# [0,1,2,4,6,7,8,9],[3,5]
# [1,2,3,4,5,6,7,8],[0,9]
# [0,1,2,3,4,5,7,9],[6,8]
# [0,2,3,4,5,6,8,9],[1,7]
kf =KFold(n_splits=5, random_state=2001, shuffle=True)
# 保存当前最好的K值和对应的准确值
best_k = ks[0]
best_score = 0
# 循环每一个K值
for k in ks:
curr_score=0
for train_index, valid_index in kf.split(X):
#每一折的训练以及计算准确率
clf = KNeighborsClassifier(n_neighbors=k)
clf.fit(X[train_index], y[train_index])
curr_score = curr_score + clf.score(X[valid_index], y[valid_index])
#求5折的平均准确率
avg_score = curr_score/5
if avg_score > best_score:
best_k = k
best_score = avg_score
print("现在的最佳准确率:%.2f"%best_score, "现在的最佳K值 %d"%best_k)
print("最终最佳准确率:%.2f"%best_score, "最终的最佳K值 %d"%best_k)
打印结果:
(150, 4) (150,)
现在的最佳准确率:0.96 现在的最佳K值 1
现在的最佳准确率:0.96 现在的最佳K值 1
现在的最佳准确率:0.97 现在的最佳K值 5
现在的最佳准确率:0.98 现在的最佳K值 7
现在的最佳准确率:0.98 现在的最佳K值 7
现在的最佳准确率:0.98 现在的最佳K值 7
现在的最佳准确率:0.98 现在的最佳K值 7
现在的最佳准确率:0.98 现在的最佳K值 7
最终最佳准确率:0.98 最终的最佳K值 7
5、算法特点
KNN是一种非参的,惰性的算法模型。什么是非参,什么是惰性呢?
非参的意思并不是说这个算法不需要参数,而是意味着这个模型不会对数据做出任何的假设,与之相对的是线性回归(我们总会假设线性回归是一条直线)。也就是说KNN建立的模型结构是根据数据来决定的,这也比较符合现实的情况,毕竟在现实中的情况往往与理论上的假设是不相符的。
惰性又是什么意思呢?想想看,同样是分类算法,逻辑回归需要先对数据进行大量训练(tranning),最后才会得到一个算法模型。而KNN算法却不需要,它没有明确的训练数据的过程,或者说这个过程很快。
5.1 KNN算法优点
- 简单易用,相比其他算法,KNN算是比较简洁明了的算法。即使没有很高的数学基础也能搞清楚它的原理。
- 模型训练时间快,上面说到KNN算法是惰性的,这里也就不再过多讲述。
- 预测效果好。
- 对异常值不敏感
5.2 KNN算法缺点
- 对内存要求较高,因为该算法存储了所有训练数据
- 预测阶段可能很慢
- 对不相关的功能和数据规模敏感
?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 工作中的软件、插件等技术大全(建议收藏,持续更新)
- 工业数据的特殊性和安全防护体系探索思考
- ZFX山海近三个月在FX110现大量用户投诉!
- 制作一个简单HTML静态网页(HTML+CSS)
- 通过全网热议的“通义舞王”,你对AI有什么奇思妙想?
- 图搜api按图搜索淘宝商品接口拍立淘API接口精准搜索商品代码调用案例
- 当系统盘存储空间不足时,该如何操作?
- go语言10进制与16进制转换
- SQLAlchemy快速入门
- Go语言Gin框架 IP限流限速