Tarjan-割点问题

前言

之前介绍Tarjan算法求强连通分量时，提到了代码段中对于访问过的邻接点应用其时间戳来更新追溯值，不是说用追溯值更新会导致答案错误，而是为了和后续双连通分量的代码保持统一。学习双连通分量求解，要先了解割点个割边的概念，本文来介绍割点。

关于Tarjan算法求解强连通分量，见：SCC-Tarjan算法，强连通分量算法，从dfs到Tarjan详解-CSDN博客

---

割点定义

在一个无向图中，如果将一个点及与该点相连的边删除后连通分量会被断开分为 2 个及以上，这个点就是一个割点（也称割顶）。

割点的求解

割点的定义十分简洁，其求解思路也十分简单，同样是基于Tarjan-SCC算法（详见）。

割点判定定理

• 如果x不是根节点，当搜索树上（注意条件为搜索树上）存在x的一个子节点y，满足low[y] ≥ dfn[x]，那么x就是割点。
• 如果x是根节点（即连通分量中最早访问节点），当搜索树上存在至少两个子节点y1，y2，满足上述条件，那么x就是割点。

在证明之前，我们先通过下面例子来理解一下：

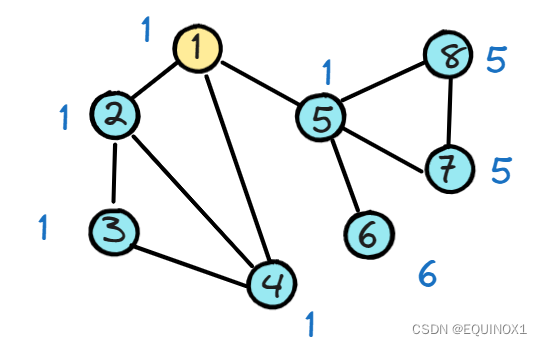
为了方便说明，我们给的示例中点的编号与dfn值相同，旁边标注的是low值

**对于定理1：**定理1用于判定非根割点，对于示例，我们观察节点5，其邻接点low值均不小于5，我们发现割掉5后，原本的连通分量{1，2，3，4，5，6，7，8}变为了{1，2，3，4}、{6}和{7，8}

**对于定理2：**定理1用于判定根割点，那我们直接看根1，我们发现2，4，5均满足，此时满足条件的邻接点数目大于1，我们删掉1后得到了{2，3，4}和{5，6，7，8}

---

证明（非严谨）

定理1：

对于非根节点x，当搜索树上（注意是搜索树上而非原图上）存在x的一个子节点y，满足low[y] ≥ dfn[x]，那么说明子节点y在不通过x的情况下是无法抵达比x时间戳更早的节点的，这也就说明了x是所在环的环顶，否则如果不是环顶，那么y一定可以通过环顶到达更早时间戳。

那么由于环顶x非根，所以x和环外节点有边连接，割掉x后必然能够多分出至少一个连通分支。

定理2：

先说明为什么搜索树上x只有一个子节点满足条件不是割点。

由于根节点只跟自己连通分量内节点有边，与其他连通分量的点无边，当割掉根x，那么对于原连通分量来说并不会分为多个连通分量，因为原来根x的唯一满足条件的子节点y会成为新的根，因为除了y的其它子节点一定可以抵达y，它们仍是一个连通分量。

那如果至少有两个子节点（我们不妨设为y，z）满足呢？

那么对于yz而言，它们不通过x的情况下彼此互相不可达，即处于两个环，否则搜索过程中二者时间戳早的那个一定可以访问晚的那个，这样就不存在y、z都满足条件了。

那么割掉x后，x所在环和y所在环由于失去x而互相不可达，分为了两个连通分量，当满足条件的子节点大于2时，则会更多。

我们以下图为例

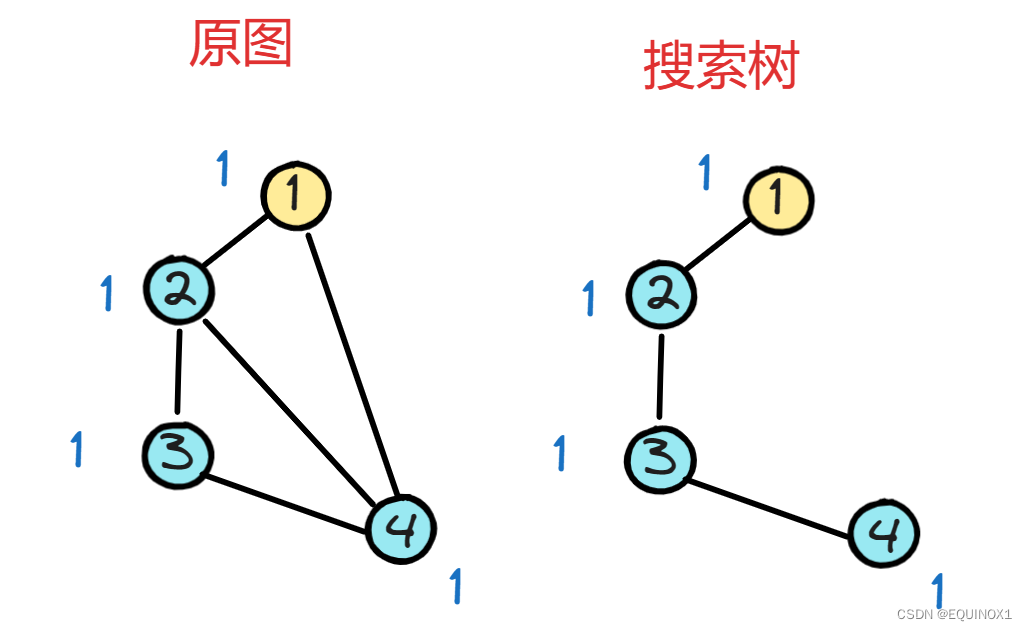
我们观察右图搜索树，发现1只有2一个子节点，割掉1后，仍为一个连通分量。

---

算法实现

求解割点算法实现十分简单，我们要判定搜索树上节点的子节点，即我们深搜过程中访问子节点过程中还未访问的子节点，我们只要在这个过程中进行割点判断即可。

算法流程

• 对x深搜，打时间戳
• 访问子节点y
• y未访问，则对y深搜，更新low[x]
  • 如果low[y] >= low[x]，若x不是根，那么x为割点
  • 否则符合条件子节点数目child+1，如果child>1，x为割点
• y已访问，更新low[x]

代码详解

#define N 20010
#define M 200100
//链式前向星
struct edge
{
    int v, nxt;
} edges[M];
int head[N]{0}, idx = 0;
void addedge(int u, int v)
{
    edges[idx] = {v, head[u]};
    head[u] = idx++;
}

int dfn[N]{0}, low[N]{0}, tot = 0, root; 
// dfn 时间戳 low节点所能访问的最小时间戳 tot为访问节点的时间戳编号
bitset<N> cut;//cut标记数组

void tarjan(int x)
{
    dfn[x] = low[x] = ++tot;
    int y, child = 0;
    for (int j = head[x]; ~j; j = edges[j].nxt)
    {
        y = edges[j].v;
        if (!dfn[y])//搜索树上子节点
        {
            tarjan(y);
            low[x] = min(low[x], low[y]);
            if (low[y] >= dfn[x])
            {
                child++;
                if (x != root || child > 1)
                    cut[x] = 1;
            }
        }
        else
        {
            low[x] = min(low[x], dfn[y]);
        }
    }
}

再看SCC

此时对于割点代码段中else语句“low[x] = min(low[x], dfn[y]);”应该理解为什么用父节点dfn值更新而非low值了，如果用low值，说明子节点可以越过父节点到达更早节点，这显然是不合理的，如下图：

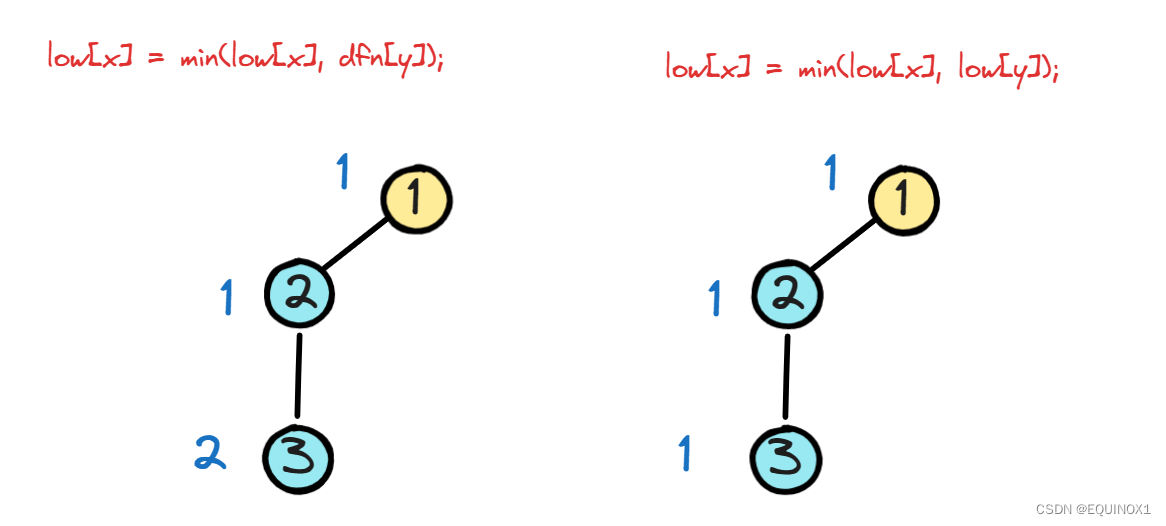
那么我们SCC算法中用low[x] = min(low[x], dfn[y])是否会影响SCC算法正确性呢？自然不会，不然你OJ怎么过的，因为这不会影响我们根的判定，而且也不会影响从栈中获取SCC内的节点。

到这里，对于Tarjan求SCC应该就再无疑惑了。

OJ练习

P3388 【模板】割点（割顶） - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)