算法训练营Day40

#Java #动态规划

Feeling and experiences：

单词拆分：力扣题目链接

给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。

注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

示例 1：

输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。

把这道题转化为完全背包的问题后，就很简单了：

class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
       
    //字符串s 能否用集合中的字符串拼接而成

    //创建dp数组 含义：字符串长度为i dp[i]是否能由1个或多个字符串组成
    boolean []dp = new boolean[s.length()+1];
    //初始化dp数组
    dp[0] = true; //dp【0】 一定要设置为true ，不然后面递推不了

    //判断组合问题还是排列问题 （这里是排列问题）
    //先背包再物品
    for(int i = 1;i<=s.length();i++){
        for(int j = 0;j<i;j++){
            //取得截取单词
            String word = s.substring(j,i);
            //截取的单词是否能在集合中找到
            if(wordDict.contains(word) && dp[j]){
                dp[i] = true;
            }
        }
    }
    return dp[s.length()];

    }
}

这里可以再优化一下，用到Set集合，把原本的wordDict集合用 HashSet 集合实现，这样可以提高效率！

1. 动态规划数组?(dp)?的定义：
dp[i]?表示字符串?s?的前?i?个字符是否可以由?wordDict?中的单词组合而成。

2. 初始化：
dp[0]?被初始化为?true，意味着一个空字符串总是可以由单词列表组成（即不选择任何单词）。

3. 状态转移：
对于?dp[i]（i?为?1?到?s.length()），遍历?j?从?0?到?i-1。对于每个?j，检查以下两个条件：
? s.substring(j,?i)（即从索引?j?到?i-1?的子串）是否在?wordDict?中；
? dp[j]?是否为?true，意味着?s?的前?j?个字符可以由单词列表组成。
如果这两个条件都满足，意味着可以通过选择?s.substring(j,?i)?和前面的某种组合来形成?s?的前?i?个字符。因此，将?dp[i]?设置为?true。

打家劫舍：力扣题目链接

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

示例 1：

输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
?    偷窃到的最高金额 = 1 + 3 = 4 。

这道题不难理解，但是解法第一次不容易想到

GPT提供了一个很好的思路：

1. 分析子问题：
对于每个房子?i，盗贼有两个选择：偷或不偷。如果盗贼选择偷这个房子，那么就不能偷前一个房子；如果选择不偷，那么他可以考虑偷前一个房子。这构成了一个子问题：对于每个房子，盗贼需要根据前一个房子的选择来做出决定。

2. 寻找子问题间的关系（状态转移方程）：
? 如果盗贼偷第?i?个房子，则他不能偷第?i-1?个房子，因此当前的最大金额是?dp[i-2]?+?nums[i]（即到第?i-2?个房子时的最大金额加上当前房子的金额）。
? 如果盗贼不偷第?i?个房子，则当前的最大金额是?dp[i-1]（即到第?i-1?个房子时的最大金额，不受当前房子影响）。
? 对于每个房子，我们需要选择上述两种情况中金额较大的那一个，即?dp[i]?=?max(dp[i-1],?dp[i-2]?+?nums[i])。

3. 考虑初始条件：
? 如果只有一个房子，那么最大金额就是这个房子中的金额。
? 如果有两个房子，那么最大金额是这两个房子中金额较大的那一个。

4. 构建最终解：
根据递推公式从前向后计算，直到最后一个房子，此时?dp?数组的最后一个元素就是最大的偷窃金额。

class Solution {
    public int rob(int[] nums) {
            //动态规划
            //建立dp数组，定义为dp[i]为最多
            int len = nums.length;
            int []dp = new int[len];
            //特殊情况
            if(nums.length==0){
                return 0;
            }
            if(nums.length==1){
                return nums[0];
            }
            //初始化前两家最优
            dp[0] = nums[0];
            dp[1] = Math.max(nums[0],nums[1]);
            //递推
            

           //遍历，填充数组
            for(int i =2;i<len;i++){
                //第一种情况，拿最后一个，就不能拿倒数第二个
           
                //第二种情况，不拿最后一个
            dp[i] =Math.max(dp[i-1],dp[i-2]+nums[i]);
            }
            return dp[len-1];
    }
}

?

打家劫舍II：力扣题目链接

你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警 。

给定一个代表每个房屋存放金额的非负整数数组，计算你 在不触动警报装置的情况下 ，今晚能够偷窃到的最高金额。

示例?1：

输入：nums = [2,3,2]
输出：3
解释：你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。

这道题与上一题的不同在于：（代码随想录中的图示）

?

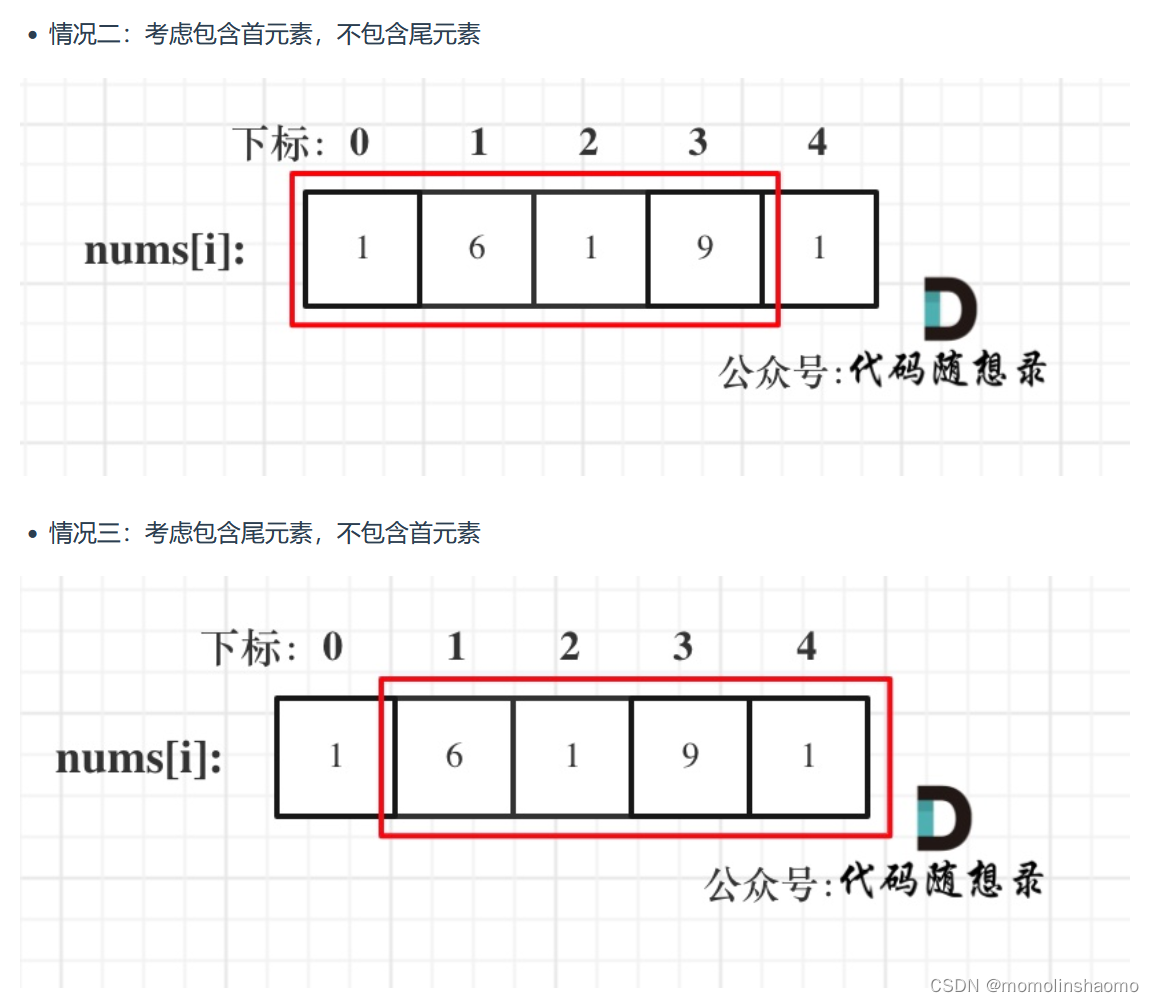根据之前的代码进行修改：
?

class Solution {
    public int rob(int[] nums) {
        int len = nums.length;
        
        // 特殊情况处理
        if (len == 0) return 0;
        if (len == 1) return nums[0];
        if (len == 2) return Math.max(nums[0], nums[1]);

        // 分两种情况考虑，一种是不包括最后一个房子，一种是不包括第一个房子
        return Math.max(robRange(nums, 0, len - 2), robRange(nums, 1, len - 1));
    }

    // 辅助函数，用来计算在指定范围内能偷到的最大金额
    private int robRange(int[] nums, int start, int end) {
        if (start == end) return nums[start];

        int[] dp = new int[nums.length];
        dp[start] = nums[start];
        dp[start + 1] = Math.max(nums[start], nums[start + 1]);

        for (int i = start + 2; i <= end; i++) {
            dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
        }

        return dp[end];
    }
}

考虑从第一个房子到倒数第二个房子的情况（不包括最后一个房子）。

考虑从第二个房子到最后一个房子的情况（不包括第一个房子）。

且将新火拭新茶，

诗酒趁年华。

Fighting！
?

?