代码随想录算法训练营29期|day 23 任务以及具体安排

class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if (root == null) {
            return null;
        }
        if (root.val < low) {
            return trimBST(root.right, low, high);
        }
        if (root.val > high) {
            return trimBST(root.left, low, high);
        }
        // root在[low,high]范围内
        root.left = trimBST(root.left, low, high);
        root.right = trimBST(root.right, low, high);
        return root;
    }
}

本题的关键是要明白删除节点，不能直接返回null，要考虑如果是小于low的话，要考虑删除节点的右子树，如果大于high的话，要考虑删除节点的左子树。

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return sortedArrayToBSTHelper(nums,0,nums.length);
        
    }
    public TreeNode sortedArrayToBSTHelper(int[] nums, int begin , int end){
        if(begin == end) return null;

        int middle = (begin+end)/2;
        TreeNode root = new TreeNode(nums[middle]);        
        root.left = sortedArrayToBSTHelper(nums, begin, middle);
        root.right = sortedArrayToBSTHelper(nums, middle+1, end);

        return root;

    }
}

本题相对比较简单，关键是思考清楚begin和end的开闭情况。

思路：每次取中间的值作为父节点，然后遍历middle左边的区间和右边的区间。

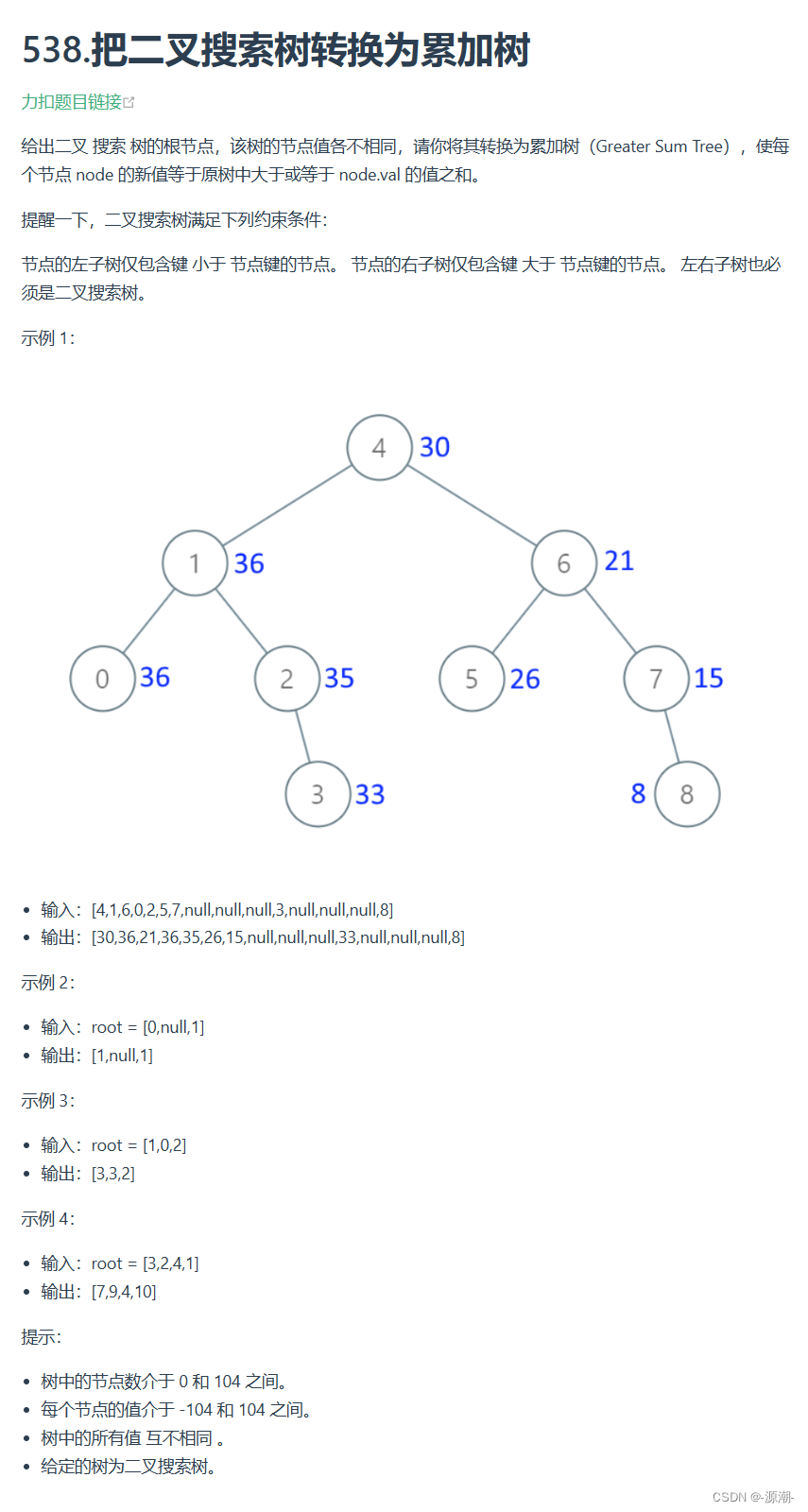
class Solution {
    int sum;
    public TreeNode convertBST(TreeNode root) {
        sum = 0;
        convertBST1(root);
        return root;
    }

    // 按右中左顺序遍历，累加即可
    public void convertBST1(TreeNode root) {
        if (root == null) {
            return;
        }
        convertBST1(root.right);
        sum += root.val;
        root.val = sum;
        convertBST1(root.left);
    }
}

思路：本题的关键是右中左的遍历顺序，用一个指针sum记录前一个节点的值，与当前节点相加。