算法导论复习（八）| 基本图算法

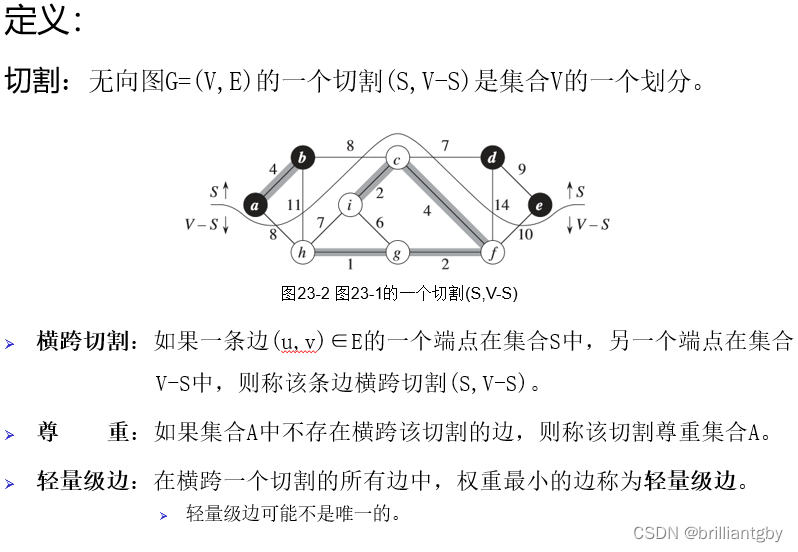
权重图：图中的每条边都带有一个权重的图。
权重值通常以权重函数 ω:E→R 给出。
邻接表

• 权重值ω(u,v)存放在u的邻接链表结点中。

邻接矩阵

• 邻接矩阵A[u][v] = ω(u,v)。
• 若(u,v)不是E中的边，A[u][v] =NIL，或∞、0。

最小生成树

kruskal算法

Kruskal算法找安全边的方法：在所有连接森林中两棵不同树的边中，找权重最小的边(u,v)。

时间复杂度：O(E lg E)

prim算法

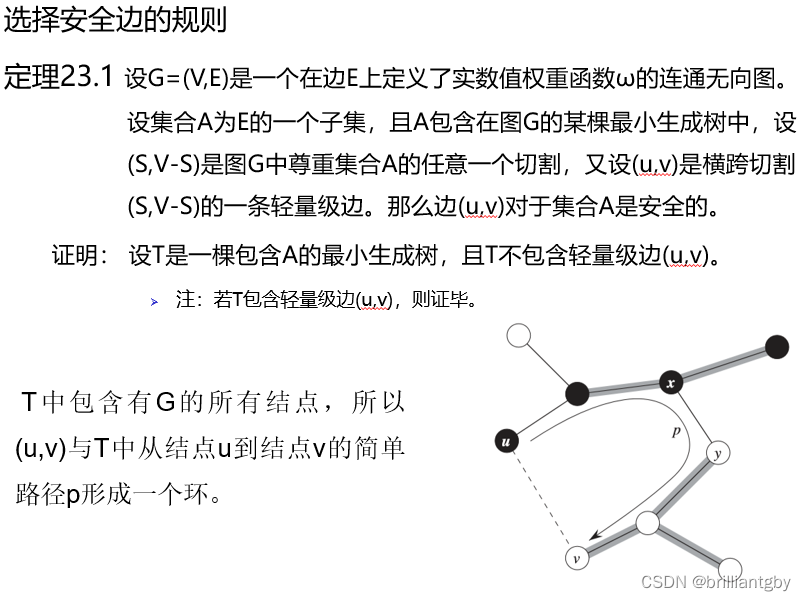
Prim算法的每一步是在连接集合A和A之外的结点的所有边中，选择一条轻量级边加入到A中。所加入的边对于A也是安全的。
Prim算法的基本性质：集合A中的边总是构成一棵树。

Prim算法的时间复杂度：O(V lg V +E lg V )=O(E lg V )。

---

单源最短路径

给定一个图G=(V,E)，找出从给定的源点s∈V到其它每个结点v∈V的最短路径。
最短路径的最优子结构
? 最短路径具有最优子结构性：两个结点之间的一条最短路径的任何子路径都是最短的。

引理24.1 给定一个带权重的有向图G=(V,E)和权重函数ω:E→R。设p=<v0,v1,…,vk>为从结点v0到结点vk的一条最短路径，并且对于任意的i和j，0≤i≤j≤k，设pij=<vi,vi+1,…,vj>为路径p中从结点vi到结点vj的子路径，则pij是从结点vi到结点vj的一条最短路径。

松弛

三角不等式

bellman-ford算法

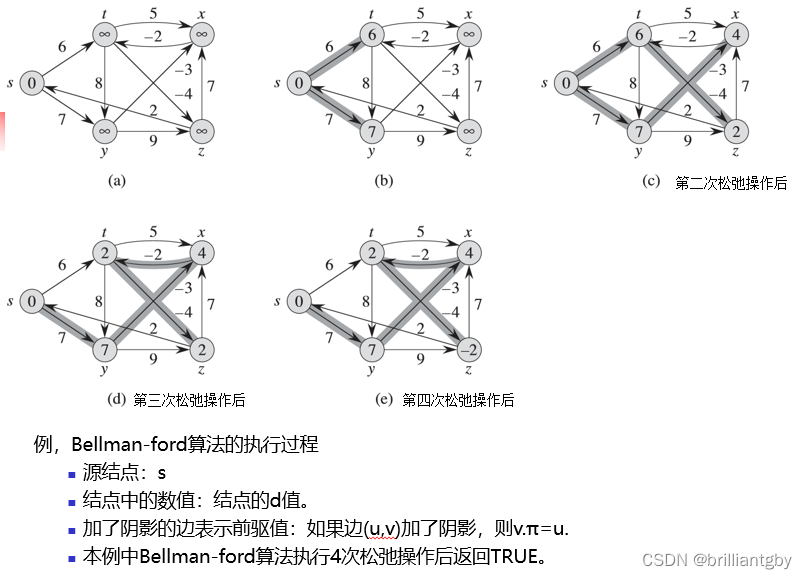
Bellman-ford算法总的运行时间O(VE)。

dijkstra算法

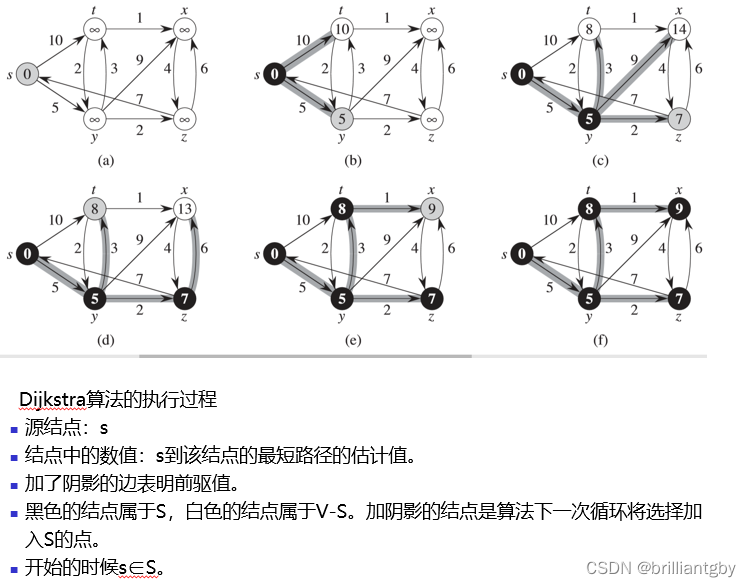
如果用线性数组实现，每次找d最小的结点u需要O(V)的时间，所以算法的总运行时间为O(V²+E)=O(V²)。

---

差分约束

技巧：

• 约束图中，不等关系为 x_i-x_j<=b_k 时，从vj到vi有一条权值为bk的有向边。
• 解为所添加结点v0到各个结点的单源最短路径。

---

所有结点对的最短路径问题

递归表达式

矩阵乘法的修改。

Floyd-Warshall算法

简记：遍历k,比较ik+kj。在矩阵中画十字，看两边比较。

算法描述：

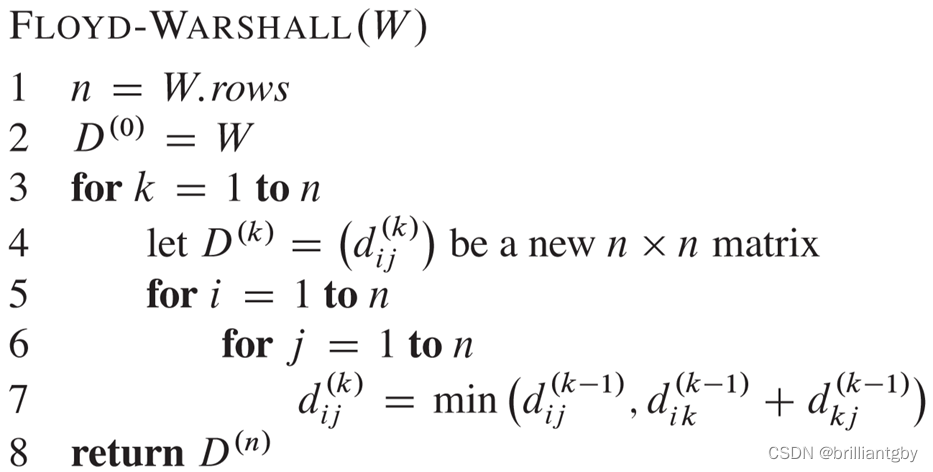
Wn╳n：权重邻接矩阵；
Dn╳n：最短路径权重矩阵
FLOYD-WARSHALL自底向上地完成D矩阵的计算。

johnson算法

---