LeetCode 2132. 用邮票贴满网格图：二维前缀和 + 二维差分

【LetMeFly】2132.用邮票贴满网格图：二维前缀和 + 二维差分

力扣题目链接：https://leetcode.cn/problems/stamping-the-grid/

给你一个?m x n?的二进制矩阵?grid?，每个格子要么为?0?（空）要么为?1?（被占据）。

给你邮票的尺寸为?stampHeight x stampWidth?。我们想将邮票贴进二进制矩阵中，且满足以下?限制?和?要求?：

1. 覆盖所有 空?格子。
2. 不覆盖任何 被占据?的格子。
3. 我们可以放入任意数目的邮票。
4. 邮票可以相互有 重叠?部分。
5. 邮票不允许 旋转?。
6. 邮票必须完全在矩阵 内?。

如果在满足上述要求的前提下，可以放入邮票，请返回?true?，否则返回?false?。

?

示例 1：

输入：grid = [[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0]], stampHeight = 4, stampWidth = 3
输出：true
解释：我们放入两个有重叠部分的邮票（图中标号为 1 和 2），它们能覆盖所有与空格子。

示例 2：

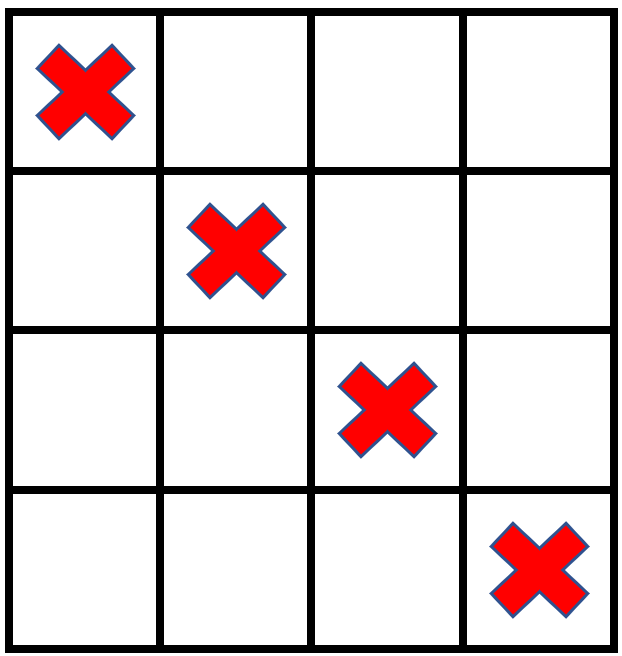
输入：grid = [[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]], stampHeight = 2, stampWidth = 2 
输出：false 
解释：没办法放入邮票覆盖所有的空格子，且邮票不超出网格图以外。

?

提示：

• m == grid.length
• n == grid[r].length
• 1 <= m, n <= 105
• 1 <= m * n <= 2 * 105
• grid[r][c] 要么是?0?，要么是?1 。
• 1 <= stampHeight, stampWidth <= 105

方法一：二维前缀和 + 二维差分

二维前缀和预处理好后，可以在$O(1)$的时间内查出任意矩形的所有元素之和。（$prefix[i+1][j+1]$是$mat[i][j]$及其左上角所有元素组成的矩阵的和）

若矩形内每个元素都加d，则可以在$O(1)$的时间内记录到差分数组中。最后能以$O(mn)$的时间还原出原数组。（按求前缀和的方式对差分数组计算，即可得到原矩阵）

因为贴邮票的次数不限，因此我们决定：能贴的下就贴。最后，看看是否还有空格即可。

具体思路：

消耗$O(mn)$的时间计算出前缀和数组。

遍历矩阵中的每个空白位置，若以这个位置为左上角可以贴邮票（通过前缀和能很快确认），则贴邮票（通过差分数组能很快记录）。

最终再消耗$O(mn)$的时间还原出贴发票后的矩阵。

• 时间复杂度$O(size(grid))$
• 空间复杂度$O(size(grid))$

AC代码

C++

class Solution {
public:
    bool possibleToStamp(vector<vector<int>>& grid, int h, int w) {
        int n = grid.size(), m = grid[0].size();
        vector<vector<int>> prefix(n + 1, vector<int>(m + 1)), diff(n + 2, vector<int>(m + 2));
        // prefix
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                prefix[i + 1][j + 1] = grid[i][j] + prefix[i][j + 1] + prefix[i + 1][j] - prefix[i][j];
            }
        }
        // stamp
        for (int i = 0; i + h - 1 < n; i++) {
            for (int j = 0; j + w - 1 < m; j++) {
                // (i, j) -> (i + h - 1, j + w - 1)
                if (!grid[i][j] && !(prefix[i + h][j + w] - prefix[i + h][j] - prefix[i][j + w] + prefix[i][j])) {
                    diff[i + 1][j + 1]++;
                    diff[i + 1][j + w + 1]--;
                    diff[i + h + 1][j + 1]--;
                    diff[i + h + 1][j + w + 1]++;
                }
            }
        }
        // un-diff
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                diff[i + 1][j + 1] += diff[i][j + 1] + diff[i + 1][j] - diff[i][j];
                if (!grid[i][j] && !diff[i + 1][j + 1]) {
                    return false;
                }
            }
        }
        return true;
    }
};

Python

# from typing import List

class Solution:
    def possibleToStamp(self, grid: List[List[int]], h: int, w: int) -> bool:
        n, m = len(grid), len(grid[0])
        prefix = [[0] * (m + 1) for _ in range(n + 1)]
        diff = [[0] * (m + 2) for _ in range(n + 2)]
        # get-prefix
        for i in range(n):
            for j in range(m):
                prefix[i + 1][j + 1] = grid[i][j] + prefix[i + 1][j] + prefix[i][j + 1] - prefix[i][j]
        # stamp
        for i in range(n - h + 1):
            for j in range(m - w + 1):
                # (i, j) -> (i + h - 1, j + w - 1)
                if not grid[i][j] and not (prefix[i + h][j + w] + prefix[i][j] - prefix[i + h][j] - prefix[i][j + w]):
                    diff[i + 1][j + 1] += 1
                    diff[i + h + 1][j + 1] -= 1
                    diff[i + 1][j + w + 1] -= 1
                    diff[i + h + 1][j + w + 1] += 1
        # un-diff
        for i in range(n):
            for j in range(m):
                diff[i + 1][j + 1] += diff[i + 1][j] + diff[i][j + 1] - diff[i][j]
                if not grid[i][j] and not diff[i + 1][j + 1]:
                    return False
        return True

同步发文于CSDN，原创不易，转载经作者同意后请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/135002925