南邮最优化期末复习

发布时间：2023年12月25日

image-20231205135043160

image-20231211172030749

黄金分割法

image-20231211183748214

单纯形法（大M法）

  • 求min, σ找最小，终止条件全部大于0 θ找最小，且不能为负数
  • 求max, σ找最大，终止条件全部小于0 θ找最小，且不能为负数

image-20231204171630879

  • 例题

image-20231204171906518

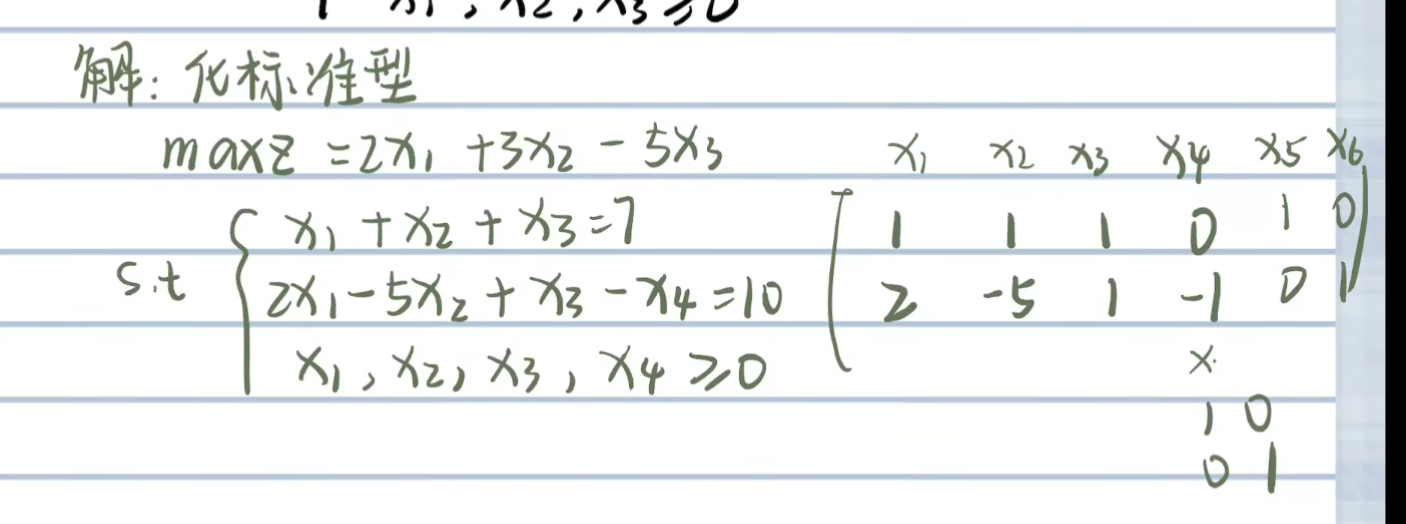
image-20231204171936437

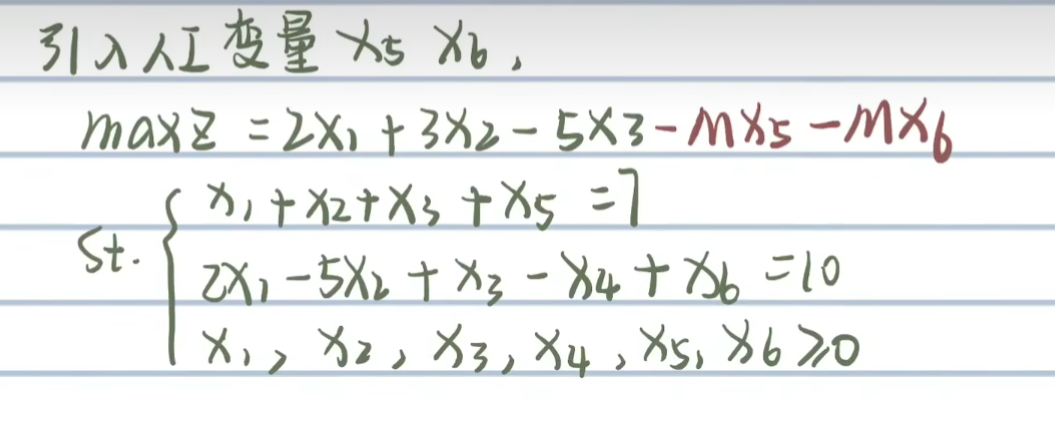
image-20231204172000229

image-20231204172027357

image-20231204172127234

二阶段单纯形法想·

image-20231204174413044

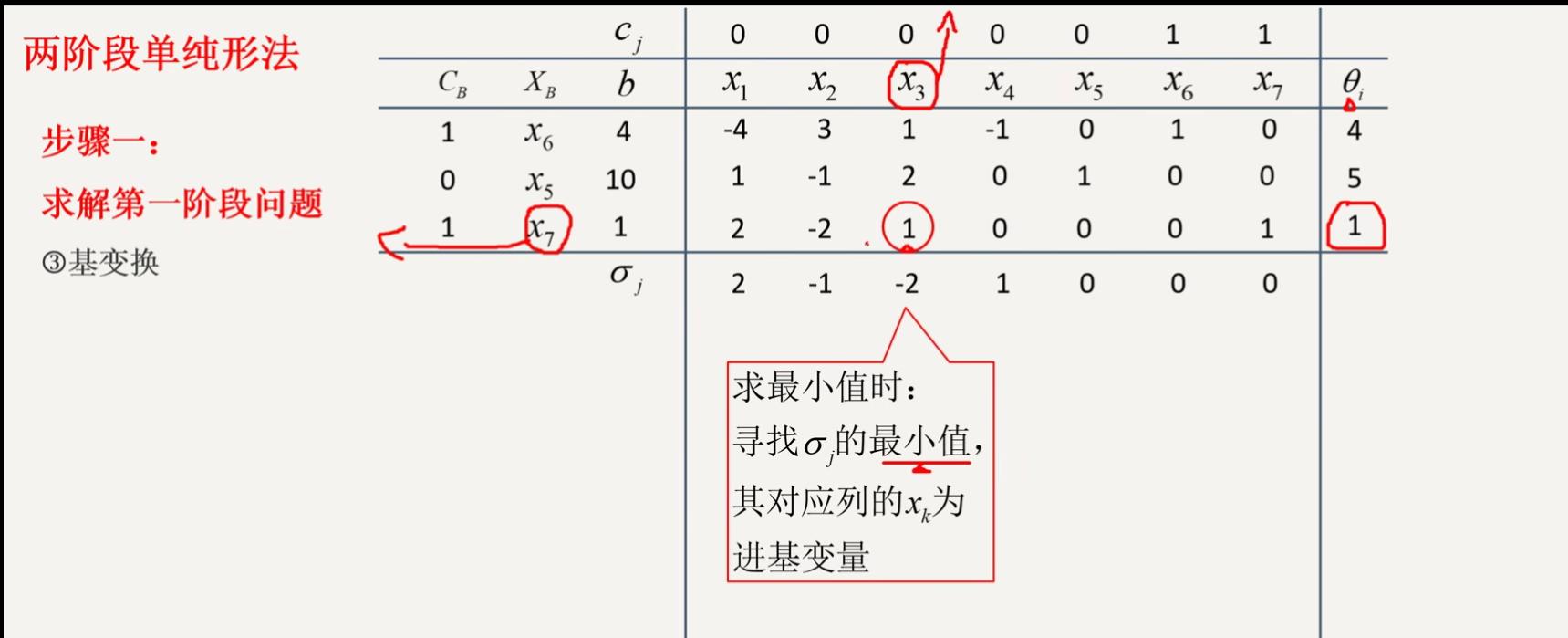
image-20231204174858998

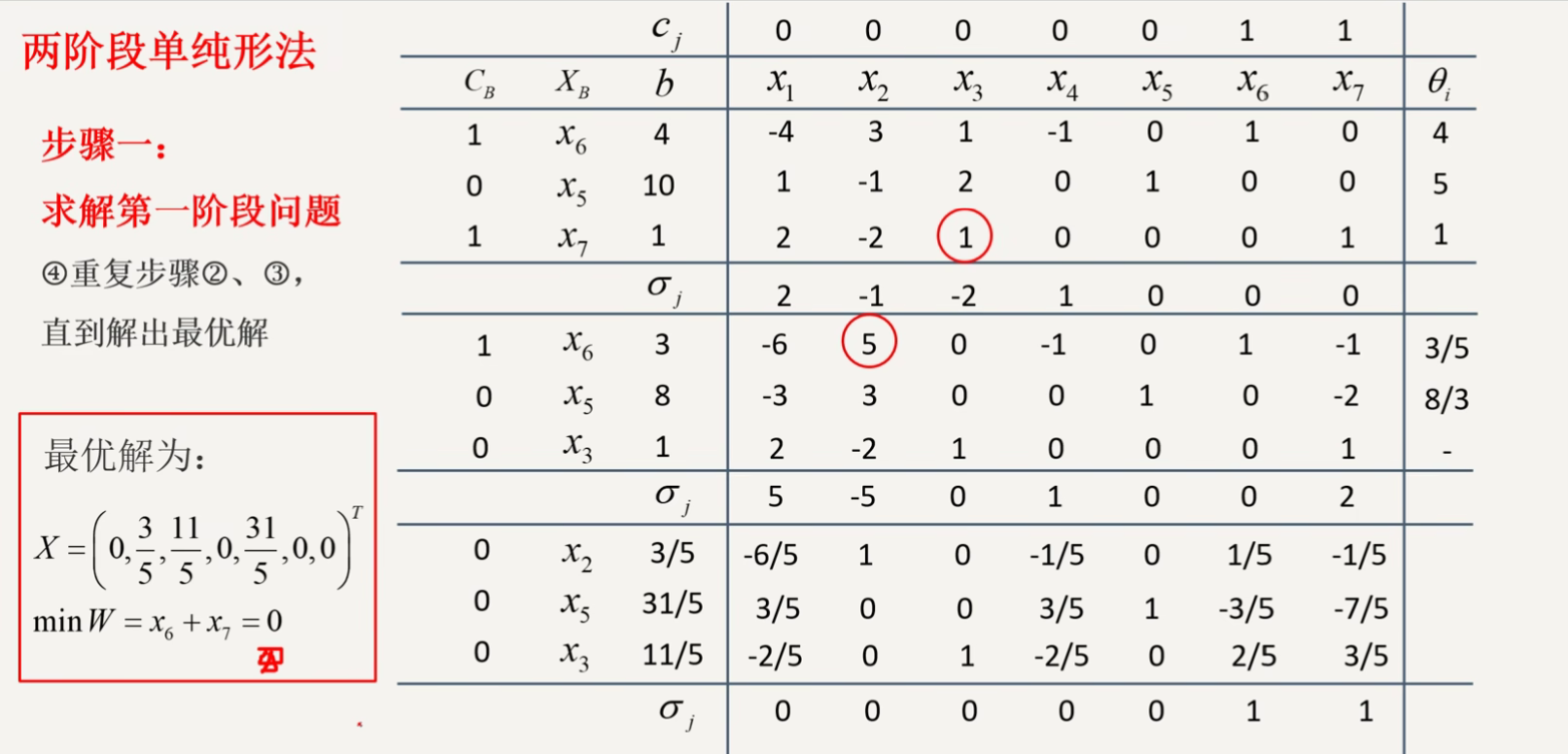
image-20231204175230802

image-20231204175252489

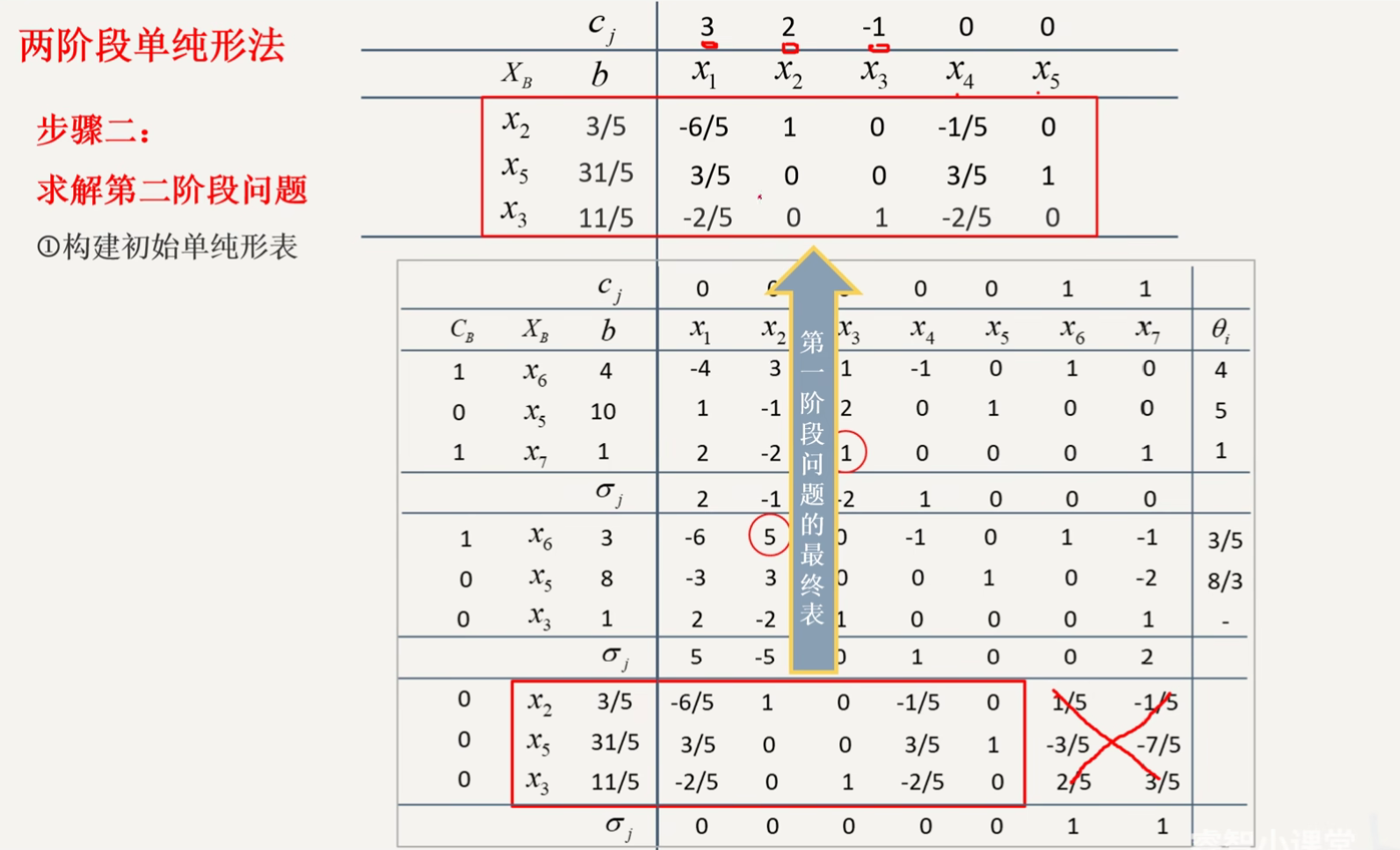
image-20231204175459199

image-20231204175816838

分支定界法（第二章）

image-20231206153208532

image-20231206153228876

image-20231206153255452

image-20231206153310284

image-20231205143027215

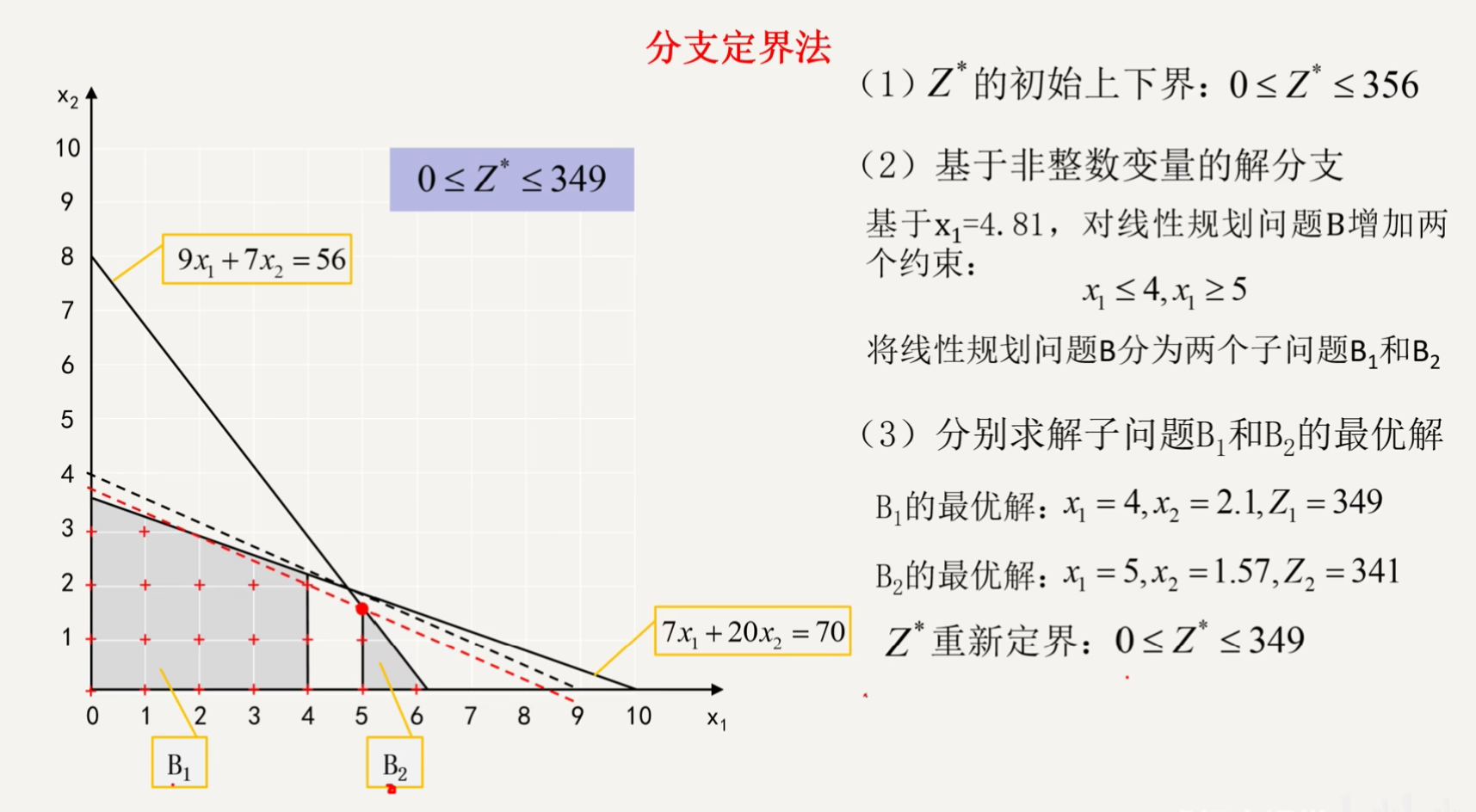
image-20231205143103017

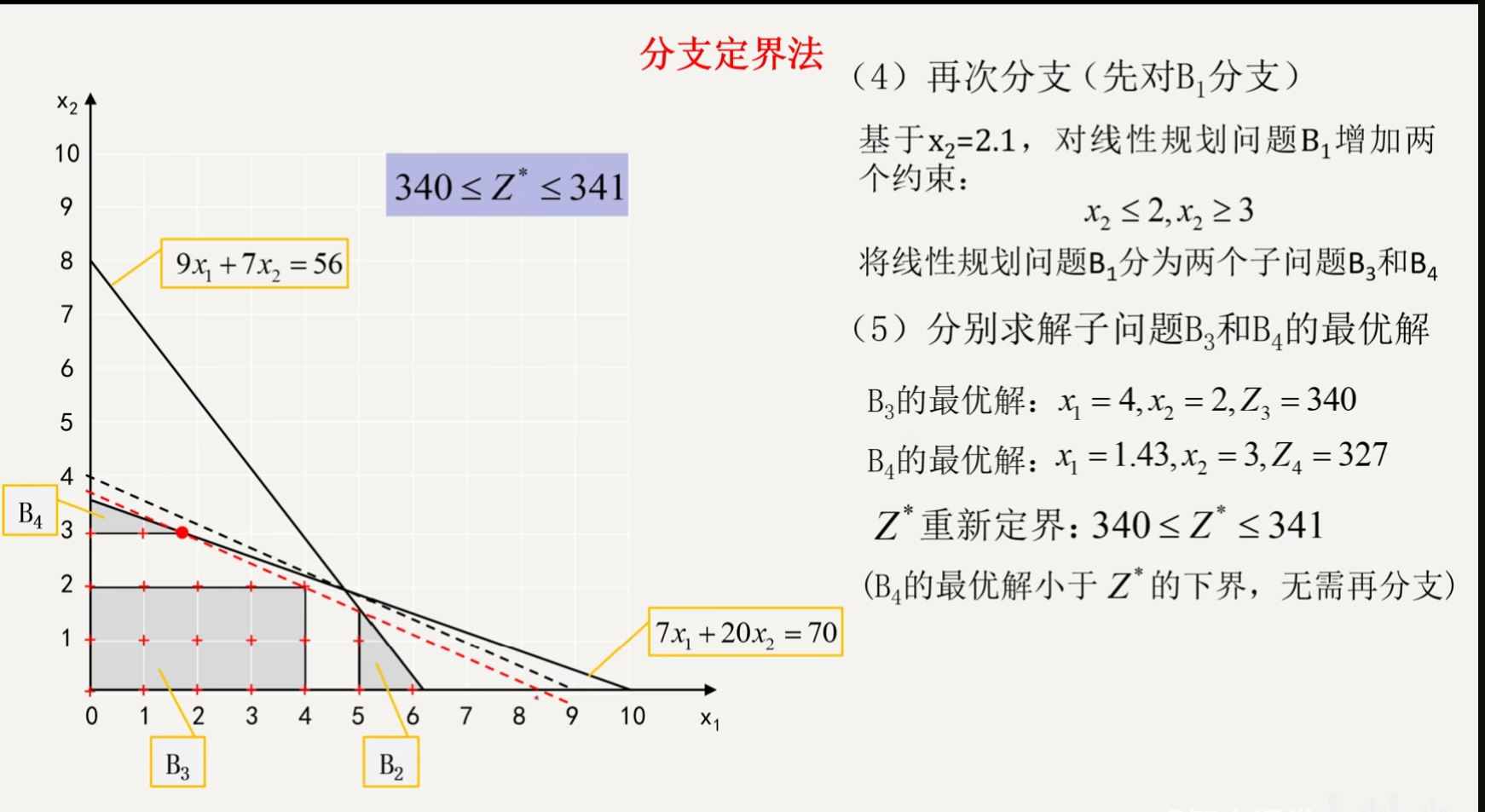
image-20231205143138342

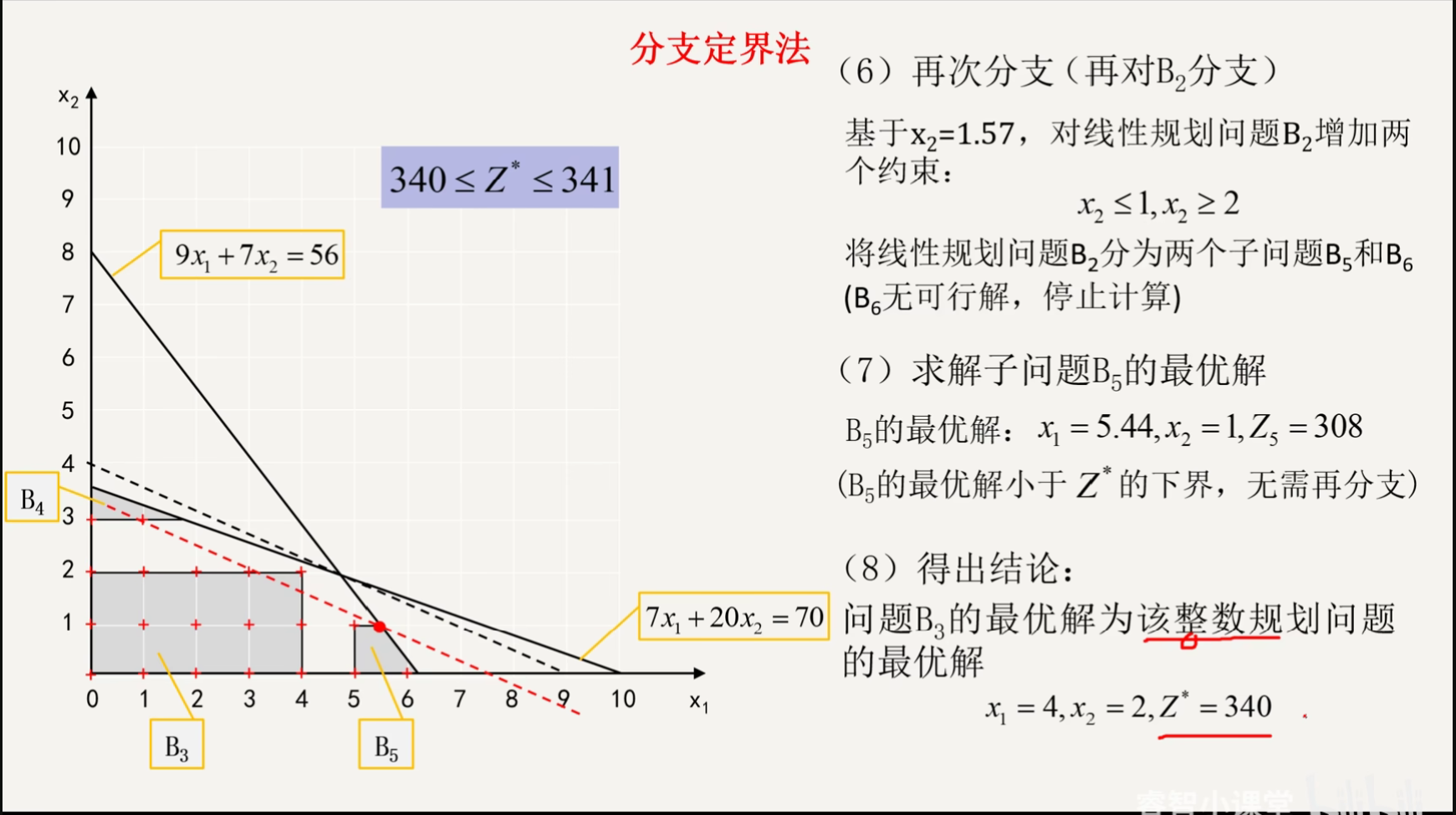
image-20231205143202940

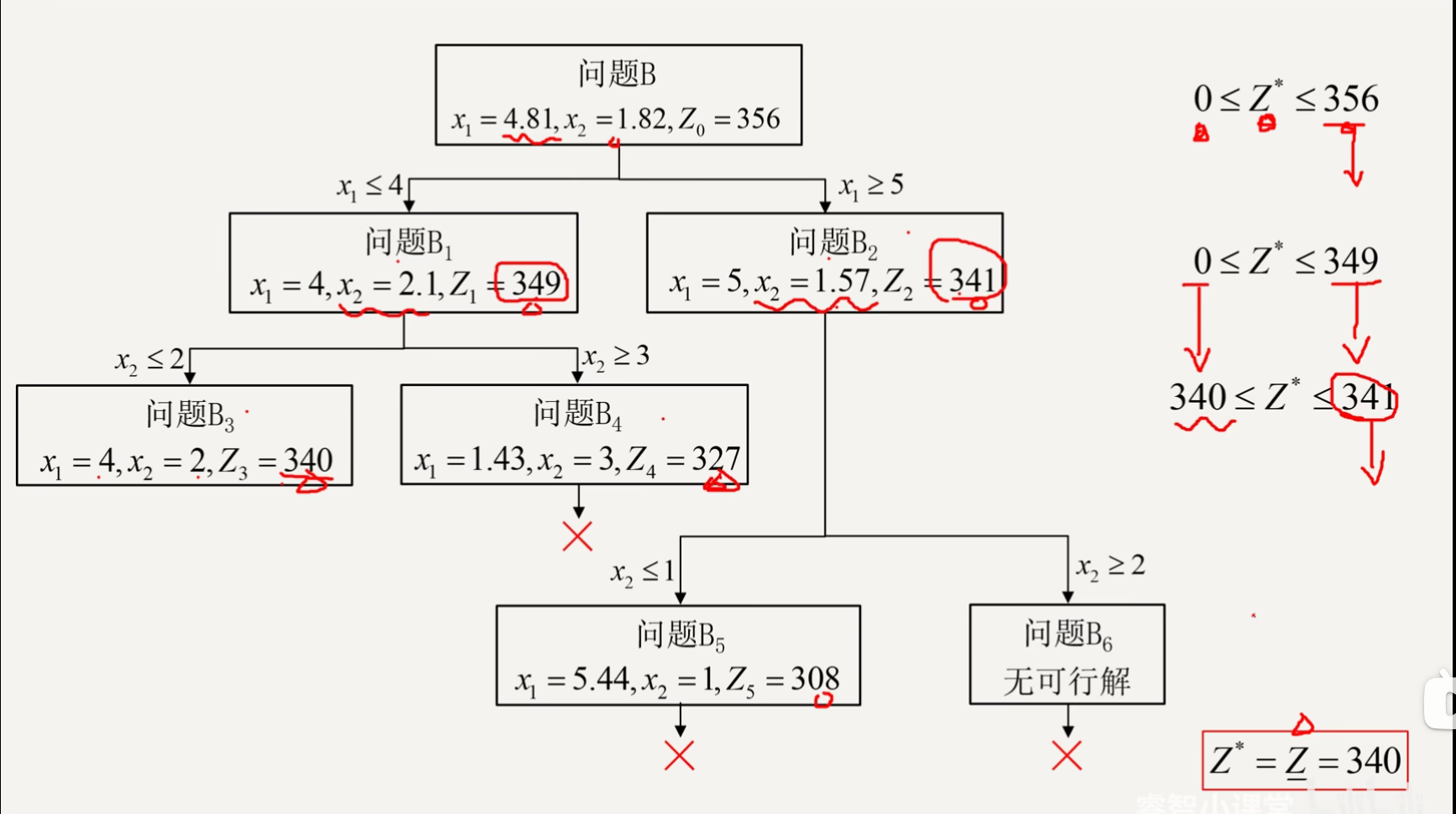
image-20231205142957938

割平面法（第二章）

image-20231205144458943

image-20231205144207597

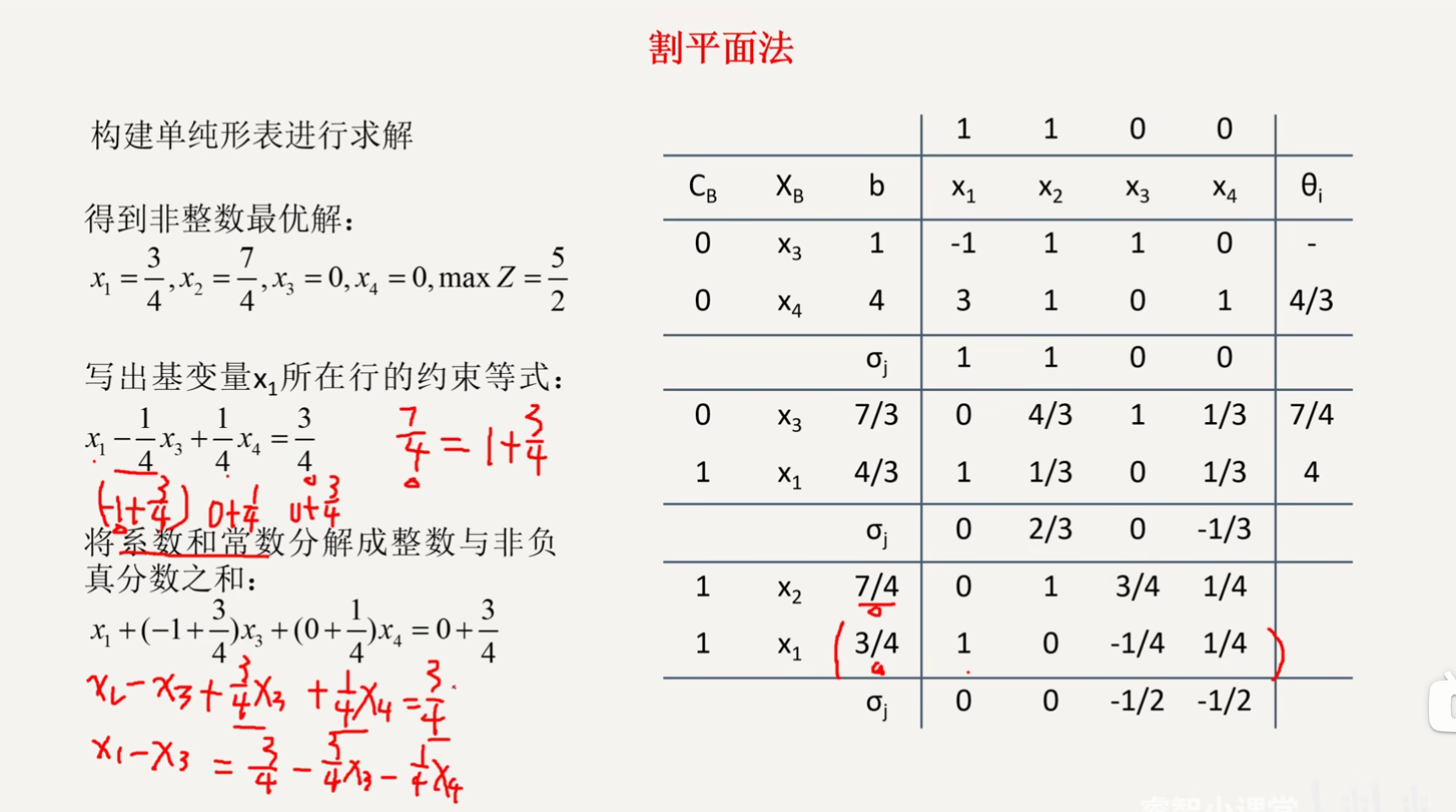
image-20231205145209637

image-20231205145604276

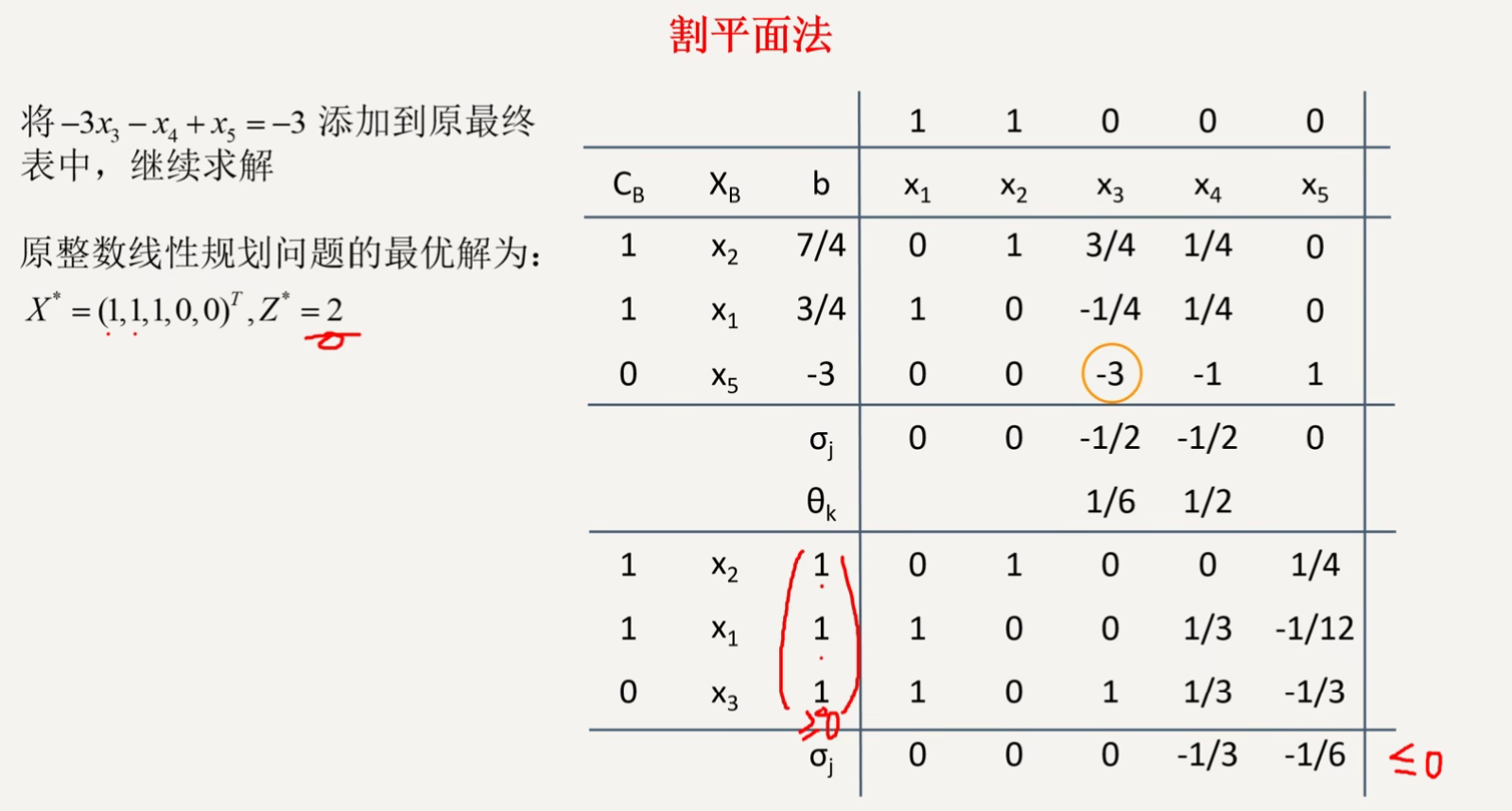
image-20231205145958825

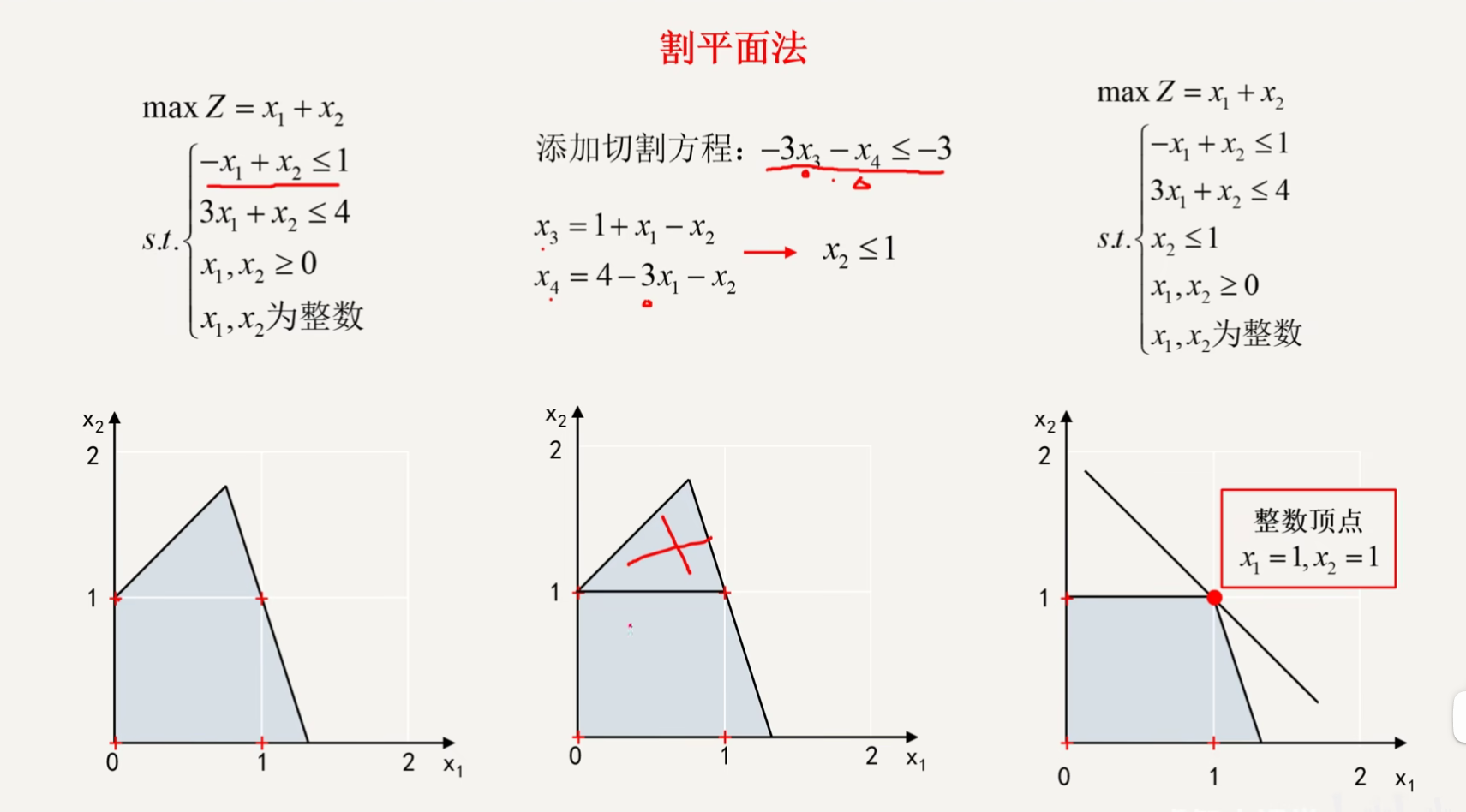
image-20231205150132267

最速下降法（第三章）

image-20231205175227853

image-20231205180202660image-20231205180249178

Newton法(第三章)

image-20231206161240822

共轭方向法FR，PRP（第三章）

image-20231206165402155

image-20231206165528757

  • PRP算法

区别只在于β的计算方法不同

image-20231206170435867

拟Newton法(DFP)（第三章）

image-20231206173914994

image-20231206173931583

外罚函数法（第四章）

image-20231211135323593

image-20231211135404866

image-20231211135459305

image-20231211135548295

image-20231211135618320

image-20231211135656474

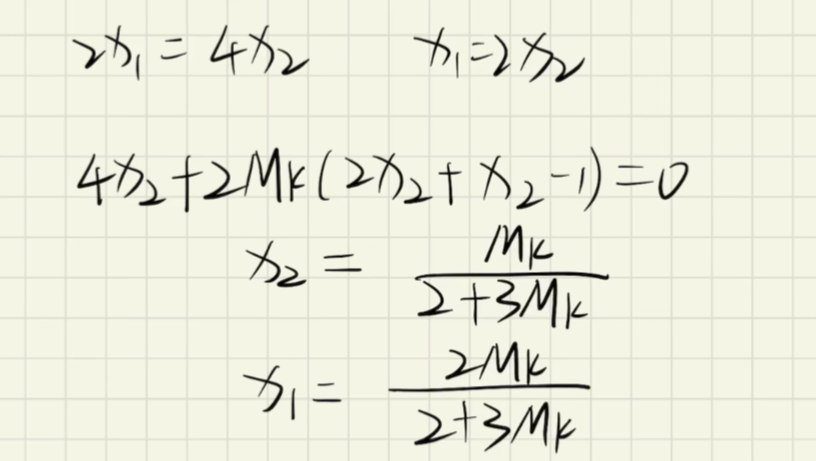
image-20231211135724737

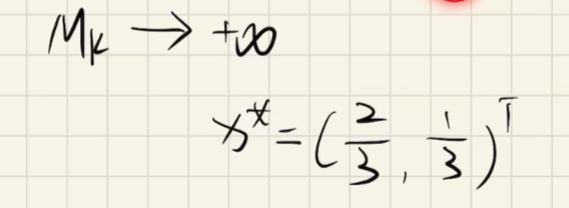
image-20231211135751453

内罚函数法（第四章）

image-20231211141715516

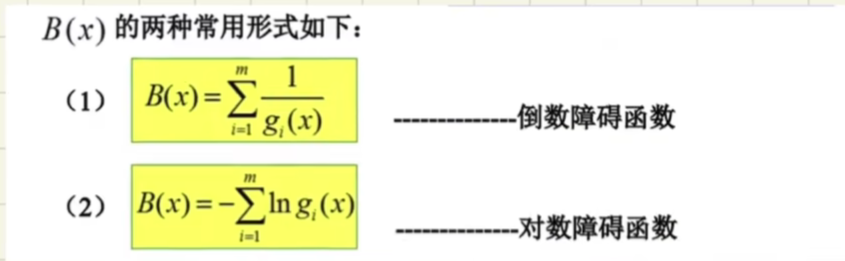
image-20231211141725394

image-20231211141743708

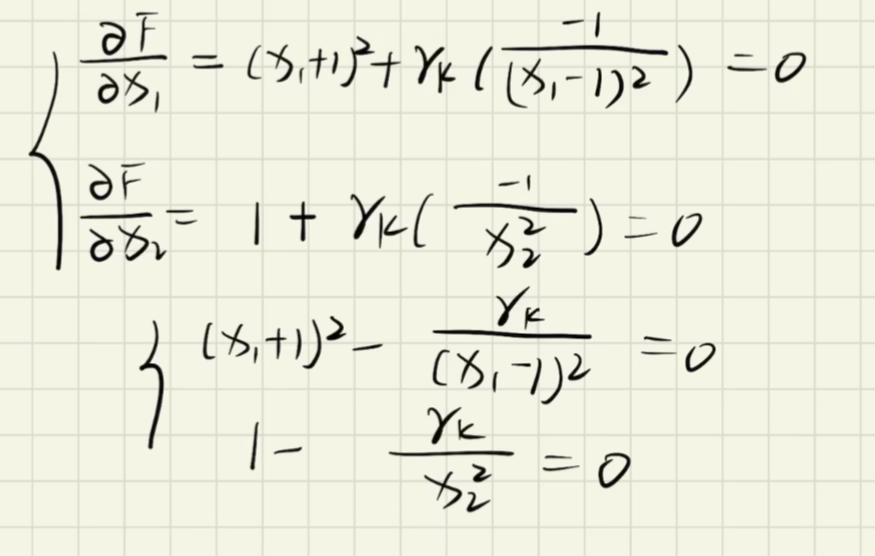
image-20231211141802637

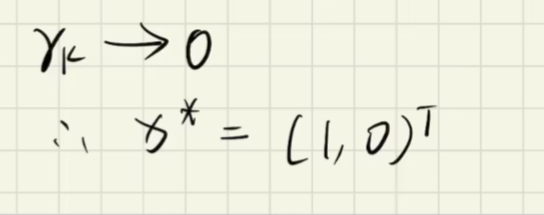
image-20231211141826511

乘子法(等式约束部分)

image-20231211142946490

image-20231211143005323

image-20231211143025371

等式约束二次规划

image-20231211150601464

image-20231211150617725

image-20231211150639563

相关概念

1. 凸集

image-20231211154029709

image-20231211155813936

2. 凸组合

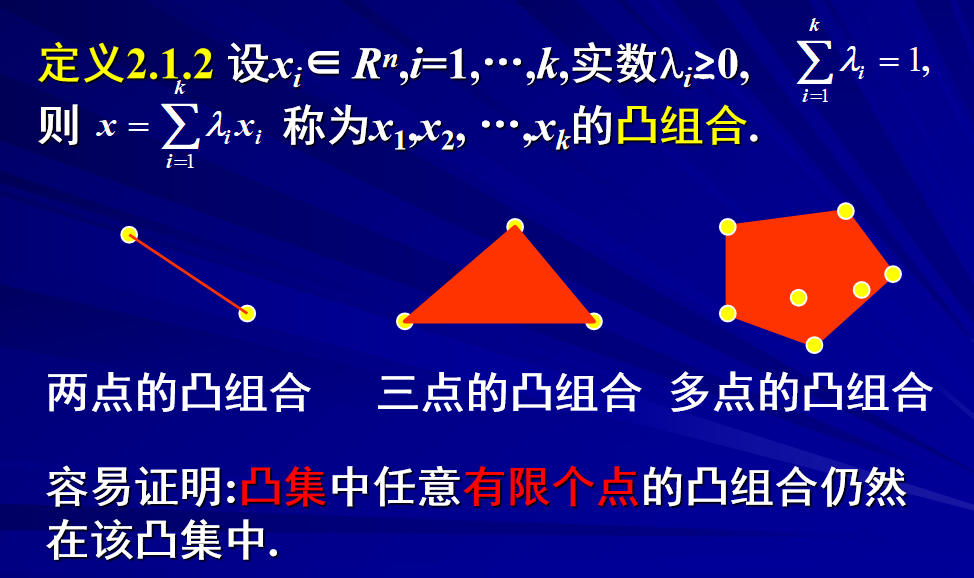
image-20231211160104504

3. 极点

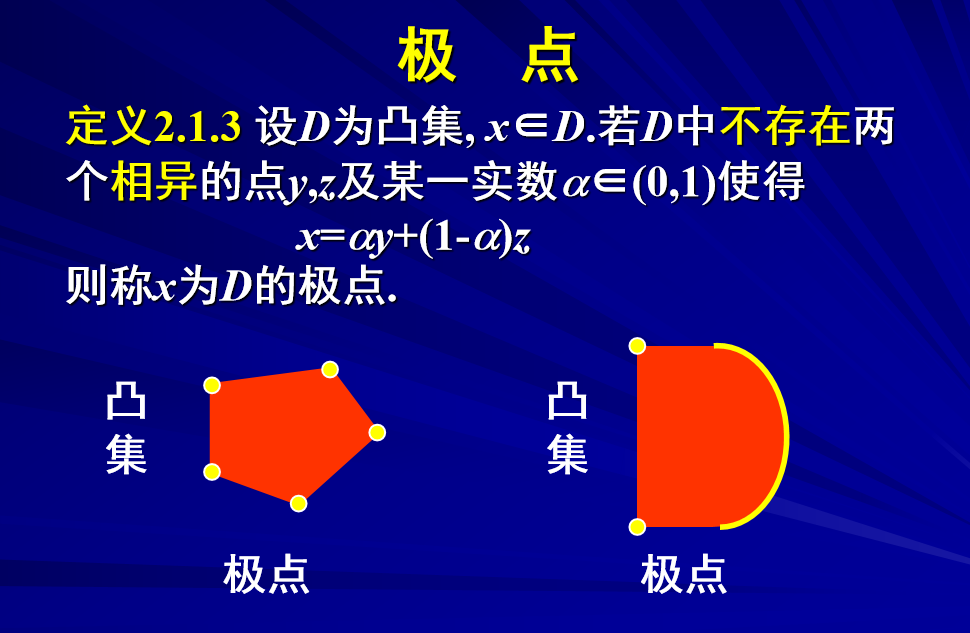
image-20231211160132052

4. 凸函数

image-20231211160307186

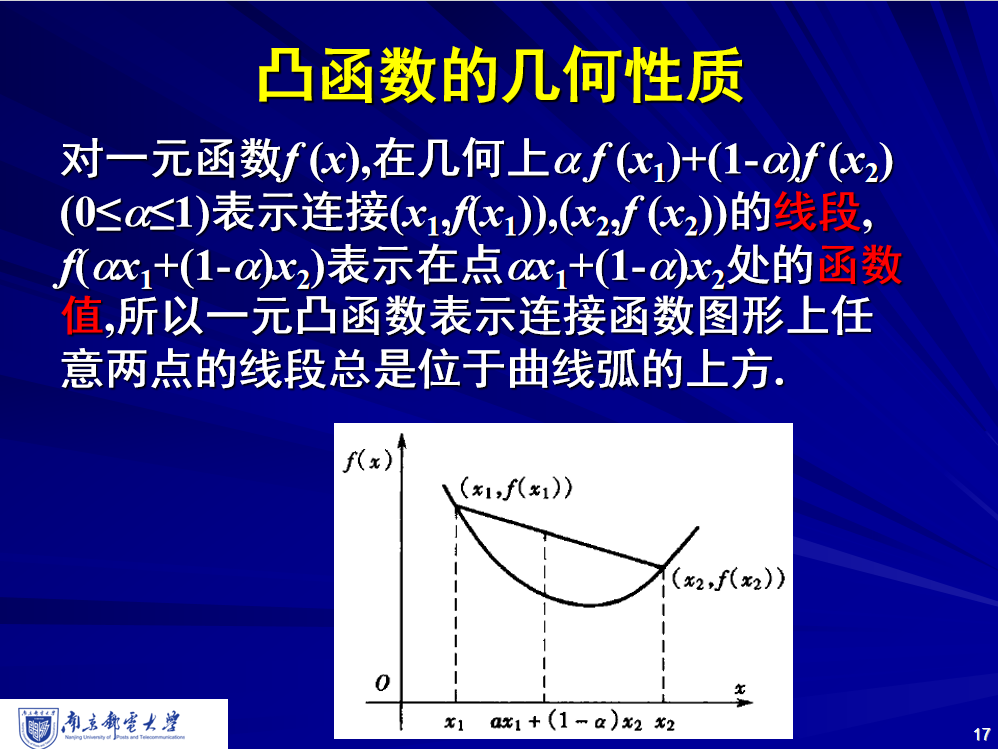
image-20231211160322883

5. 基

image-20231211162055960

KKT条件

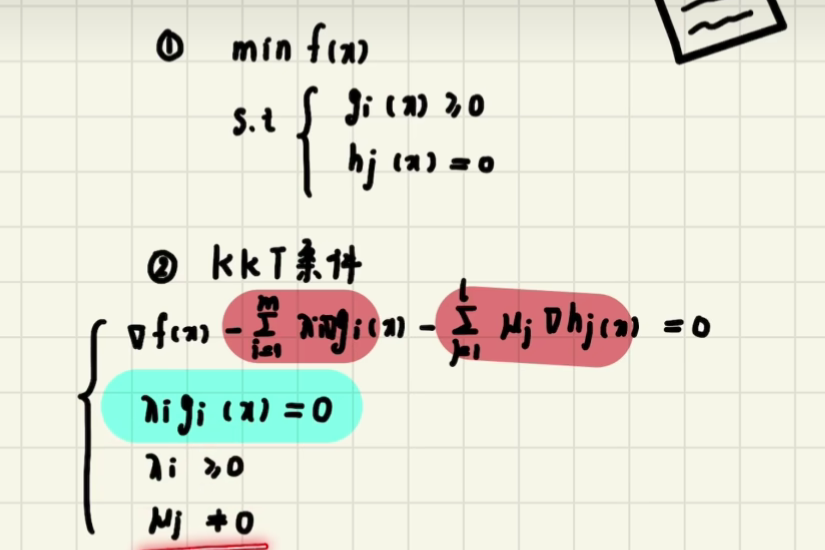
image-20231211163314263

image-20231211163422223

image-20231211163555795

求KT点

image-20231211164354521

image-20231211164428790

image-20231211164506195

image-20231211164533686

image-20231211164601472

image-20231211164626897

习题笔记

1. 对偶问题
  • 变量和约束相互对应
  • 大同小异
  • 约束和变量是相反的（约束相同，变量就相反）

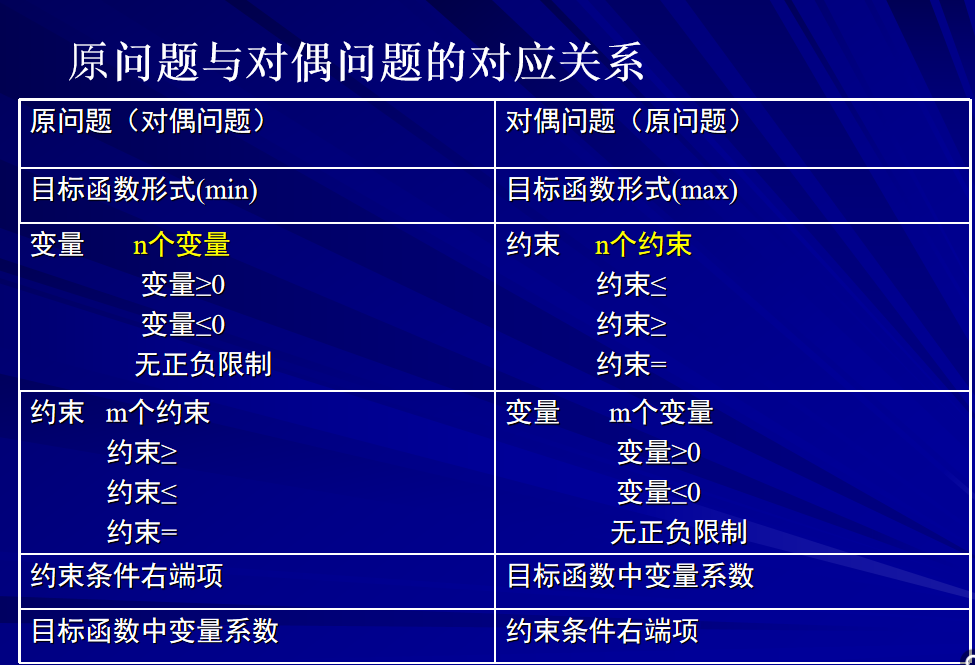
image-20231211182941385

image-20231211175023088

2. 知识点
  • 在最速下降法，Newton 法，FR 方法，PRP 方法，DFP 方法，BFGS 方法中不具备二

次终止性的算法为 最速下降法

  • 影子价格向量就是对偶规划最优解

image-20231216172027692

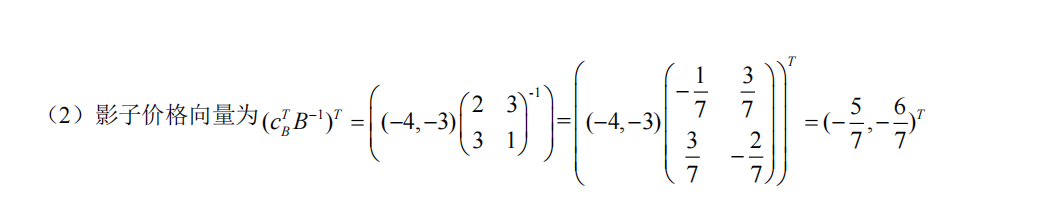
image-20231216172043176

  • 外罚函数法 M 趋近于 无穷， 内罚函数法 r 趋近于 0 ，乘子法 σ > 0
3.可行下降方向

image-20231216162522026

image-20231212182905100

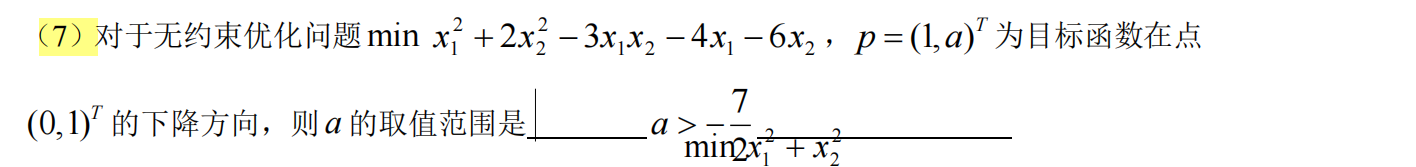
image-20231212143050348

image-20231212170645144

4. 证明题

image-20231216180518717

image-20231216180545200

文章来源:https://blog.csdn.net/love521314123/article/details/135197782
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章