LIGA-Stereo:为基于立体 3D 检测器的学习 LiDAR 几何感知表示
论文代码:https://github.com/xy-guo/LIGA-Stereo
摘要
基于立体的3D检测旨在从立体图像中检测3D目标,为3D感知提供了低成本的解决方案。然而,与基于激光雷达的检测算法相比,其性能仍然较差。为了检测和定位准确的 3D 边界框,基于 LiDAR 的检测器对 LiDAR 点云的高级表示进行编码,例如准确的边界边界和表面法线方向。相反,由于立体匹配的限制,基于立体的检测器学习的高级特征很容易受到错误的深度估计的影响。
为了解决这个问题,论文提出了 LIGA-Stereo(LiDAR 几何感知立体检测器),在基于 LiDAR 的检测模型的高级几何感知表示的指导下学习基于立体的 3D 检测器。
此外,论文发现现有的基于体素的立体检测器无法从间接 3D 监督中有效地学习语义特征。因此附加一个辅助 2D 检测头来提供直接的 2D 语义监督。
上述两种策略提高了几何和语义表示能力。
论文背景
近年来,基于 LiDAR 的 3D 检测在自动驾驶和机器人技术中取得了不断提高的性能和稳定性。然而,LiDAR传感器的高成本限制了其在低成本产品中的应用。立体匹配是最常见的仅使用相机的深度感测技术。与LiDAR传感器相比,立体相机成本更低,分辨率更高,这使其成为3D感知的合适替代解决方案。立体图像的 3D 检测旨在使用估计的深度图 或隐式 3D 几何表示来检测目标。然而,与基于LiDAR的算法相比,现有的基于立体的3D检测算法的性能仍然较差。
基于 LiDAR 的检测算法将原始点云作为输入,然后将 3D 几何信息编码为中级和高级特征表示。为了检测和定位准确的 3D 边界框,模型必须学习有关目标边界和表面法线方向的鲁棒局部特征,这对于预测准确的边界框大小和方向至关重要。基于 LiDAR 的探测器学习的特征提供了精确 3D 几何结构的强大的高级总结。相比之下,由于立体匹配的限制,不准确的估计深度或隐式 3D 表示很难对目标的准确 3D 几何进行编码,尤其是对于远处的目标。此外,目标框监督仅提供目标级监督(位置、大小和方向)。
论文利用先进的激光雷达检测模型,通过模仿激光雷达模型编码的几何感知表示来指导立体检测模型的训练。与识别任务的传统知识蒸馏相比,论文没有将LiDAR模型的最终错误分类和回归预测作为“软”目标,发现这对于训练立体检测网络没有什么好处。错误的回归目标会限制边界框回归的上限精度。
相反,论文强制模型将中间特征与 LiDAR 模型的中间特征对齐,后者对场景的高级几何表示进行编码。 LiDAR 模型的特征可以提供强大且有辨别力的高级几何感知特征,例如表面法线方向和边界位置。另一方面,LiDAR 特征可以提供额外的正则化,以缓解由错误的立体预测引起的过拟合问题。
除了学习更好的几何特征之外,论文还进一步探索如何学习更好的语义特征来提高 3D 检测性能。论文提出在 2D 语义特征上附加一个辅助的多尺度 2D 检测头,而不是从间接 3D 监督中学习语义特征,它可以直接指导 2D 语义特征的学习。根据DSGN 的消融研究,基线模型深度立体几何网络(DSGN)未能有效地从额外的语义特征中受益。论文认为,由于深度估计错误,网络从间接 3D 监督中提供了错误的语义监督,而提出的直接指导可以通过更好地学习 2D 语义特征来极大地提高 3D 检测性能。实验结果表明,性能进一步提高,特别是对于自行车手等样本较少的类别。
论文相关
立体匹配
第一个深度立体算法DispNet,从基于特征的相关 cost volume 回归视差图。后来使用多阶段细化和辅助语义特征来扩展 DispNet。最先进的立体模型通过连接所有视差候选者的左右 2D 特征来构建基于特征的 cost volume ,然后应用 3D 聚合网络来预测视差概率分布。最先进的立体检测网络也通过类似的网络结构来估计深度。
基于 LiDAR 的 3D 检测
通过利用 LiDAR 传感器捕获的更准确的深度信息,使用 LiDAR 点云的 3D 检测方法通常比基于图像的方法具有更好的性能。为了从不规则和稀疏的点云中学习有效的特征,大多数现有方法采用体素化操作将点云转移到规则网格,其中3D空间首先被划分为规则3D体素或鸟瞰2D网格通过检测头的卷积进行处理。
受它们的启发,论文提出模仿 LiDAR 模型中信息丰富的特征图,以便在 3D 框注释之外提供更好的指导。
基于立体的 3D 检测
基于立体的 3D 检测算法大致可以分为三种类型:
1)基于2D的方法
首先检测2D边界框提案,然后回归实例3D框。 Stereo-RCNN 扩展了 Faster RCNN ,用于立体输入以关联左右图像。 Disp R-CNN 和 ZoomNet 结合了额外的实例分割掩模和 part location map 来提高检测质量。然而,最终的性能受到 2D 检测算法的召回限制,并且 3D 几何信息没有得到充分利用。
2)基于伪LiDAR的3D检测
首先估计深度图,然后使用现有的基于LiDAR的算法检测3D边界框。 例如,Pseudo LiDAR++ 将 stereo cost volume 调整为深度成本量,以进行直接深度估计。。然而,这些模型仅考虑几何信息,缺乏互补的语义特征。
3)基于 volume 的方法构建
3D 锚空间或从 3D 立体 volume 进行检测。 DSGN 直接构建可微分 volume 表示,对场景的隐式 3D 几何结构进行编码,用于单阶段基于立体的 3D 检测。 PLUME 直接在 3D 空间中构造几何 volume 以进行加速。论文的工作以 DSGN 作为基线模型。解决了 DSGN 中存在的几个关键问题,并大幅超越了最先进的模型。
知识蒸馏
蒸馏是由 Hinton 等人首先提出的。 [1]通过使用大型教师网络预测中的“软化标签”来监督学生网络来进行模型压缩。进一步从“软化标签”来看,中间层的知识为教师提供了更丰富的信息。最近,知识蒸馏已成功应用于检测和语义分割。知识也可以跨模态转移。
[1] Geoffrey Hinton, Oriol Vinyals, and Jeff Dean. Distilling the knowledge in a neural network. arXiv preprint arXiv:1503.02531, 2015.
论文方法
在这项工作中,为了提高模型的性能,论文开发了两种策略来分别学习更好的几何和语义特征。由于立体匹配的限制,基于立体的检测器很容易出现错误的深度估计,特别是对于低纹理表面、模糊边界和遮挡区域。
相比之下,基于激光雷达的检测器学习的特征提供了强大的高级几何感知表示(准确的边界和表面法线方向)。为了最小化基于 LiDAR 的检测器和基于立体的探测器之间的差距,论文提出利用 LiDAR 模型来指导基于立体的探测器的训练,以实现更好的几何监督。此外,论文采用辅助二维语义监督来提高语义特征的学习效率。
深度立体几何网络
论文利用深度立体几何网络(DSGN)作为基线模型,它使用隐式 volumetric 表示直接检测目标。
立体空间中的 Volume
给定左右图像对
(
I
L
,
I
R
)
(\mathcal I_L,\mathcal I_R)
(IL?,IR?) 及其特征
(
F
L
,
F
R
)
(\mathcal F_L,\mathcal F_R)
(FL?,FR?),通过连接每个候选深度级别的左特征和相应的右特征来构造平面扫描 volume
V
s
t
\mathcal V_{st}
Vst?,
V
s
t
(
u
,
v
,
w
)
=
concat
[
F
L
(
u
,
v
)
,
F
R
(
u
?
f
L
d
(
w
)
s
F
,
v
)
]
(1)
\tag1 \mathcal V_{st}(u,v,w) = \text{concat} \lbrack \mathcal F_L (u,v),\mathcal F_R(u - \frac{fL}{d(w)s \mathcal F},v) \rbrack
Vst?(u,v,w)=concat[FL?(u,v),FR?(u?d(w)sFfL?,v)](1)
其中 ( u , v ) (u,v) (u,v) 是当前像素坐标。 w = 0 , 1 , ? ? ? ? w=0, 1,···· w=0,1,???? 为候选深度索引, d ( w ) = w ? v d + z min ? d(w)=w·v_d+z_{\min} d(w)=w?vd?+zmin? 为计算其对应深度的函数,其中 v d v_d vd? 为深度区间, z min ? z_{\min} zmin?为该深度的最小深度检测区域。 f f f、 L L L 和 s F s_{\mathcal F} sF? 分别是相机焦距、立体相机对的基线和特征图的步幅。使用 3D cost volume 聚合网络对 V s t \mathcal V_{st} Vst? 进行滤波后,我们获得聚合立体体积 V s t \mathcal V_{st} Vst? 和深度分布体积 P s t \mathcal P_{st} Pst?。 P s t ( u , v , : ) \mathcal P_{st}(u,v,:) Pst?(u,v,:)表示像素 ( u , v ) (u, v) (u,v) 在所有离散深度级别 d ( w ) d(w) d(w) 上的深度概率分布。
3D 空间中的体积
为了将 feature volume 从立体空间转换到正常的3D空间,将3D检测区域划分为相同大小的小体素。对于每个体素,使用特征内在函数
K
F
\boldsymbol K_{\mathcal F}
KF? 将其中心
(
x
,
y
,
z
)
(x, y, z)
(x,y,z) 投影回立体空间,以获得其重新投影的像素坐标
(
u
,
v
)
(u, v)
(u,v) 和深度索引
d
?
1
(
z
)
=
(
z
?
z
min
?
)
/
v
d
d^{?1}(z)=(z?z_{\min} )/v_d
d?1(z)=(z?zmin?)/vd?。然后,3D 空间中的 volume 被定义为重采样立体 volume 和深度概率 masked 的语义特征的串联,
V
3
d
(
x
,
y
,
z
)
=
concat
[
V
s
t
(
u
,
v
,
d
?
1
(
z
)
)
,
F
s
e
m
(
u
,
v
)
?
P
s
t
(
u
,
v
,
d
?
1
(
z
)
)
]
(2)
\tag2 \mathcal V_{3d}(x,y,z) = \text{concat}[\mathcal V_{st}(u,v,d^{-1}(z)),\mathcal F_{sem}(u,v)\cdot \mathcal P_{st}(u,v,d^{-1}(z))]
V3d?(x,y,z)=concat[Vst?(u,v,d?1(z)),Fsem?(u,v)?Pst?(u,v,d?1(z))](2)
其中 V s t \mathcal V_{st} Vst? 和 F s e m \mathcal F_{sem} Fsem? 分别提供几何和语义特征。请注意,为了简单起见,我们忽略了三线性和双线性重采样运算符。
BEV 空间和检测头的功能
然后通过将通道尺寸和高度尺寸像 DSGN 一样合并,将 3D volume
V
3
d
\mathcal V_{3d}
V3d? 重新排列为 2D 鸟瞰图 (BEV) 特征
F
B
E
V
\mathcal F_{BEV}
FBEV?。2D 聚合网络和检测头连接到
F
B
E
V
\mathcal F_{BEV}
FBEV?,以生成聚合的 BEV 特征
F
~
B
E
V
\tilde {\mathcal F}_{BEV}
F~BEV? 并分别预测最终的 3D 边界框。
训练损失分为两部分,深度回归损失和3D检测损失??,
L
b
s
l
=
L
d
e
p
t
h
+
L
d
e
t
(3)
\tag3 \mathcal L_{bsl} = \mathcal L_{depth}+ \mathcal L_{det}
Lbsl?=Ldepth?+Ldet?(3)
学习 LiDAR 几何感知表示
基于 LiDAR 的检测模型将原始点云作为输入,然后将其编码为高级特征(例如精确边界和表面法线方向)以获得精确的边界框局部化。对于基于立体的模型,由于错误的深度表示,纯粹的深度损失和检测损失不能很好地使模型学习遮挡区域、非纹理区域和远处物体的这些特征。
受上述观察的启发,论文提出使用激光雷达模型的高级几何感知特征来指导基于立体的检测器的训练。在本文中,我们利用 SECOND 作为 LiDAR “teacher”。为了使两个模型之间的特征尽可能一致,论文采用相同结构的 2D 聚合网络和检测头,如图所示。

由于LiDAR模型和立体模型的主干存在巨大差异,论文只关注如何对高级特征
F
i
m
?
{
V
3
d
,
F
B
E
V
,
F
~
B
E
V
}
\mathbb F_{im} \sube \{\mathcal V_{3d}, \mathcal F_{BEV}, \tilde {\mathcal F}_{BEV} \}
Fim??{V3d?,FBEV?,F~BEV?} 进行特征模仿,这些特征在LiDAR模型和立体模型之间具有相同的形状两个模型。
论文的模仿损失旨在最小化立体特征
F
i
m
∈
F
i
m
\mathcal F_{im} \in \mathbb F_{im}
Fim?∈Fim? 与其对应的 LiDAR 特征
F
i
m
l
i
d
a
r
F^{lidar}_{im}
Fimlidar? 之间的特征距离:
L
i
m
=
∑
F
i
m
∈
F
i
m
1
N
p
o
s
∣
∣
M
f
g
M
s
g
(
g
(
F
i
m
)
?
F
i
m
l
i
d
a
r
E
[
∣
F
i
m
l
i
d
a
r
∣
]
)
∣
∣
2
2
(4)
\tag4 \mathcal L_{im} = \sum_{\mathcal F_{im} \in \mathbb F_{im}} \frac{1}{N_{pos}}\bigg|\bigg| M_{fg}M_{sg}\bigg( g(\mathcal F_{im})-\frac{\mathcal F_{im}^{lidar}}{\mathbb E[|\mathcal F_{im}^{lidar}|]} \bigg) \bigg| \bigg|_2^2
Lim?=Fim?∈Fim?∑?Npos?1?
?
?Mfg?Msg?(g(Fim?)?E[∣Fimlidar?∣]Fimlidar??)
?
?22?(4)
其中 g g g 是内核大小为 1 1 1 的单个卷积层,后跟可选的 ReLU 层(取决于 ReLU 是否应用于 F i m l i d a r \mathcal F_{im}^{lidar} Fimlidar?)。 M f g M_{fg} Mfg? 是前景掩码,在任何真实对象框内为 1 1 1,否则为 0 0 0。 M s p M_{sp} Msp? 是 F i m l i d a r \mathcal F_{im}^{lidar} Fimlidar? 的稀疏掩码,对于非空索引为 1 1 1,否则为 1 1 1。 N p o s = ∑ M f g M s p N_{pos} =\sum M_{fg}M_{sp} Npos?=∑Mfg?Msp? 是归一化因子。请要注意的是,LiDAR 特征 F i m l i d a r \mathcal F_{im}^{lidar} Fimlidar? 通过 F i m l i d a r \mathcal F_{im}^{lidar} Fimlidar? 非零绝对值的通道期望进行归一化,以确保 L2 损失的尺度稳定性。
实验结果表明,模仿整个特征图对检测性能的提升不大,因此 M f g M_{fg} Mfg? 对于使模仿损失集中在前景物体上至关重要。实验发现 F B E V \mathcal F_{BEV} FBEV? 和 V 3 d \mathcal V_{3d} V3d? 为训练我们的立体检测网络提供了最有效的监督。
通过直接 2D 监督提升语义特征
从方程 (2) 可以看到,在将语义特征重采样到 3D 空间之前,它首先乘以 P s t \mathcal P_{st} Pst? 的深度概率(可以看作是 3D 占用掩模的估计)。
这样,语义特征仅在估计表面附近重新采样(图3中的橙色虚线)。
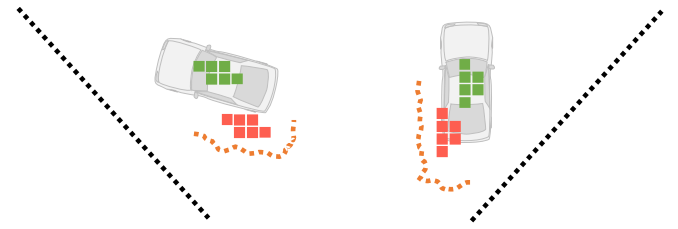
然而,当估计的深度值存在较大误差时,语义特征将被重新采样到错误的位置,如图所示。因此,重采样的语义特征偏离了真实位置,然后被分配负锚点(图中的红色方块),并且正锚点周围没有重采样的语义特征(图3中的绿色方块) 。因此,这种情况下语义特征的监督信号不正确,导致语义特征的学习效率低。
为了解决这个问题,论文添加了一个辅助的 2D 检测头来为学习语义特征提供直接监督。论文没有使用多级特征创建特征金字塔(FPN),而是只使用单个特征图
F
s
e
m
\mathcal F_{sem}
Fsem? 来构建特征金字塔,如图1(e)所示,这形成了信息“瓶颈”强制将所有语义特征编码到
F
s
e
m
\mathcal F_{sem}
Fsem? 中。将步幅为
2
2
2 的五个连续卷积层附加到
F
s
e
m
\mathcal F_{sem}
Fsem? 上,构建多级特征金字塔,然后将其连接到 ATSS 头进行 2D 检测。
由于论文发现扩张卷积和空间金字塔池化(SPP)已经产生了具有大感受野的高度语义特征,因此为了简单起见,论文忽略了 FPN 自上而下的路径。
为了确保 2D 和 3D 特征之间的语义对齐,2D 检测头应该预测重新投影的 3D 目标中心周围的高分。论文对 ATSS 的正样本分配算法做了一个小的修改。对于每个真实边界框 g g g,如果它们的中心最接近重新投影的 3D 目标中心,会从每个尺度中选择 k k k 个候选锚点,而不是样选择 2D 边界框中心。然后按照 ATSS 中的动态 IoU 阈值对候选锚点进行过滤,以分配最终的正样本。
Baseline 和训练损失的修改
论文对 DSGN 进行了一些重要修改,以获得更快、更稳健的基线模型。 1)减少通道数和层数,以减少内存消耗和计算成本。 2) 利用SECOND 检测头进行3D检测。 3)基于 Kullback-Leibler 散度将等式(6)中的 smooth-L1 深度回归损失替换为单模态深度损失。4)结合使用 L1 损失和辅助旋转 3D IoU 损失以获得更好的边界框回归。5) 将一个小型 U-Net 连接到 2D 主干,以编码全分辨率特征图以构建立体体积。
我们模型的新总体损失公式为:
L
=
L
d
e
p
t
h
+
L
d
e
t
+
λ
i
m
L
i
m
+
λ
2
d
L
2
d
,
L
d
e
t
=
L
c
l
s
+
λ
r
e
g
L
1
L
r
e
g
L
1
+
λ
r
e
g
I
o
U
L
r
e
g
I
o
U
+
λ
d
i
r
L
d
i
r
(5)
\tag5 \mathcal L = \mathcal L_{depth} + \mathcal L_{det} + \lambda_{im}\mathcal L_{im} + \lambda_{2d}\mathcal L_{2d}, \\ \mathcal L_{det} = \mathcal L_{cls}+ \lambda_{reg}^{L1} \mathcal L_{reg}^{L1}+ \lambda_{reg}^{IoU} \mathcal L_{reg}^{IoU}+ \lambda_{dir} \mathcal L_{dir}
L=Ldepth?+Ldet?+λim?Lim?+λ2d?L2d?,Ldet?=Lcls?+λregL1?LregL1?+λregIoU?LregIoU?+λdir?Ldir?(5)
其中
L
c
l
s
\mathcal L_{cls}
Lcls?,
L
r
e
g
L
1
L_{reg}^{L1}
LregL1?, 和
L
d
i
r
L_{dir}
Ldir? 是与 SECOND 中相同的分类损失、框回归损失和方向分类损失。
L
r
e
g
I
o
U
\mathcal L_{reg}^{IoU}
LregIoU? 是 3D 框预测和真实边界框之间的平均旋转
I
o
U
IoU
IoU 损失。单模态深度损失
L
d
e
p
t
h
L_{depth}
Ldepth? 的公式为
L
d
e
p
t
h
=
1
N
∑
u
,
v
∑
w
[
?
max
?
(
1
?
∣
d
?
?
d
(
w
)
∣
v
d
)
log
?
P
s
t
(
u
,
v
,
w
)
]
(6)
\tag6 \mathcal L_{depth} = \frac{1}{N} \sum_{u,v} \sum_{w} \bigg[ -\max \bigg( 1-\frac{ |d^{*} - d(w)| }{v_{d}} \bigg) \log \mathcal P_{st} (u,v,w) \bigg]
Ldepth?=N1?u,v∑?w∑?[?max(1?vd?∣d??d(w)∣?)logPst?(u,v,w)](6)
其中 d ? d^* d? 是真实深度。请注意,损失仅适用于具有有效 LiDAR 深度的像素 ( u , v ) (u, v) (u,v), N g t N_{gt} Ngt? 表示有效像素的数量。与原来的 L1 损失相比,式(6)中的损失为: 对目标分布进行更加集中的监管。
论文结论
在论文中,提出在高级几何感知 LiDAR 特征和直接语义监督的指导下学习基于立体的 3D 检测器,成功提高了几何和语义能力。模型在官方 KITTI 3D 检测基准上超越了最先进的算法超过 10.44% mAP,这缩小了基于立体和基于 LiDAR 的 3D 检测算法之间的差距。然而,基于立体的 3D 探测器仍然面临遮挡、无纹理区域和远处物体的问题。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 输电线路定位:应对复杂环境,确保电力传输畅通无阻
- 【笔记】Helm-3 主题-9 Helm高级技术
- 数据结构OJ实验10-图连通与生成树
- 每日一算法(找到字符串中第一个匹配项的下标)
- java中HashMap的七种遍历方式
- 【C初阶——指针5】鹏哥C语言系列文章,基本语法知识全面讲解——指针(5)
- Python多线程
- 中国区域30m/15天植被覆盖度数据集(2010-2020)
- [bat批处理] 一键清理 Windows10 系统垃圾
- 用C++实现Excel的Slope函数