C++刷题 -- 栈和队列
发布时间:2024年01月15日
C++刷题 – 栈和队列
1.用栈实现队列
- 一个栈自然实现不了队列功能,需要使用两个栈
- 一个输入栈,一个输出栈
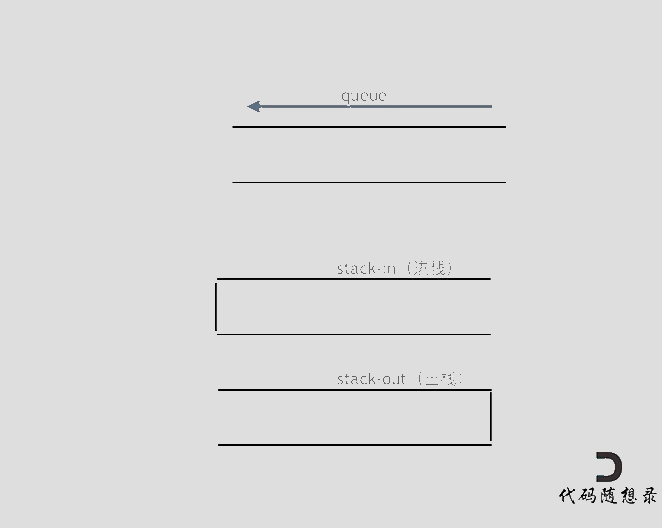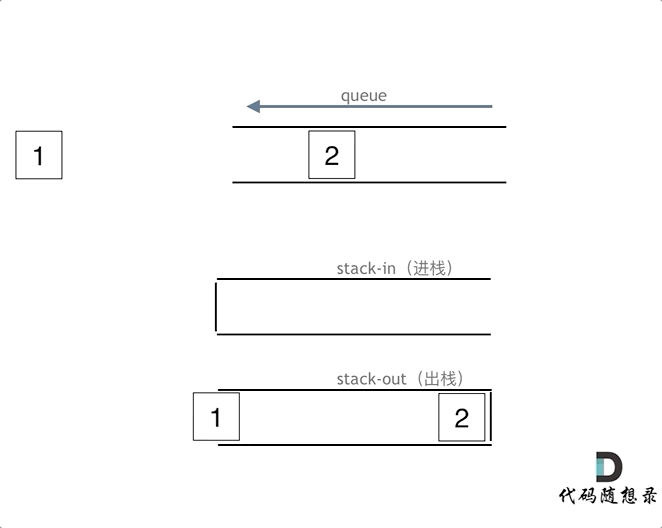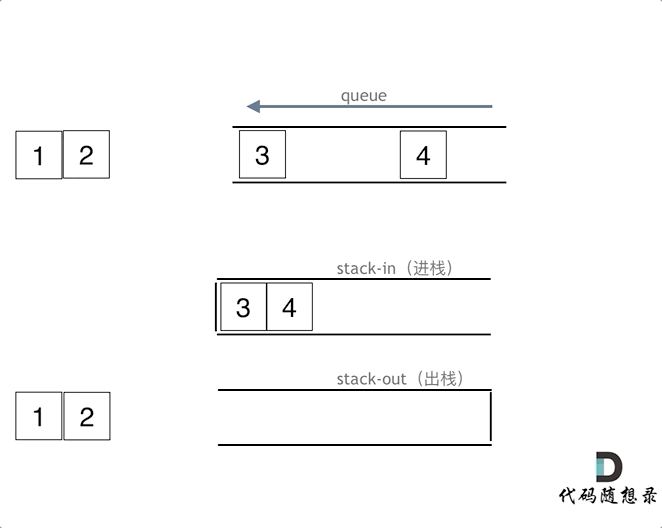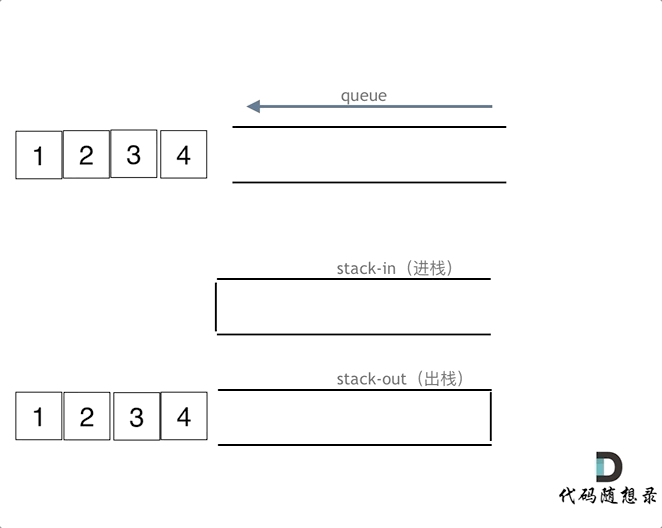
- 队列是先入先出,当队列push操作,push到输入栈的顶部
- 当队列pop操作,需要pop最先入队的元素,如果输出栈为空,就需要将当前输入栈里面的的元素全部转移到输出栈中,如果输出栈不为空,就直接pop输出栈;
- 判断队列是否为空就是判断输入栈和输出栈是否全为空;
class MyQueue {
public:
MyQueue() {
}
void push(int x) {
_in.push(x);
}
int pop() {
int ret = 0;
if(_out.empty())
{
while(!_in.empty())
{
_out.push(_in.top());
_in.pop();
}
}
ret = _out.top();
_out.pop();
return ret;
}
int peek() {
if(_out.empty())
{
while(!_in.empty())
{
_out.push(_in.top());
_in.pop();
}
}
return _out.top();
}
bool empty() {
return (_in.empty() && _out.empty());
}
private:
stack<int> _in;
stack<int> _out;
};
/**
* Your MyQueue object will be instantiated and called as such:
* MyQueue* obj = new MyQueue();
* obj->push(x);
* int param_2 = obj->pop();
* int param_3 = obj->peek();
* bool param_4 = obj->empty();
*/
2.用队列实现栈
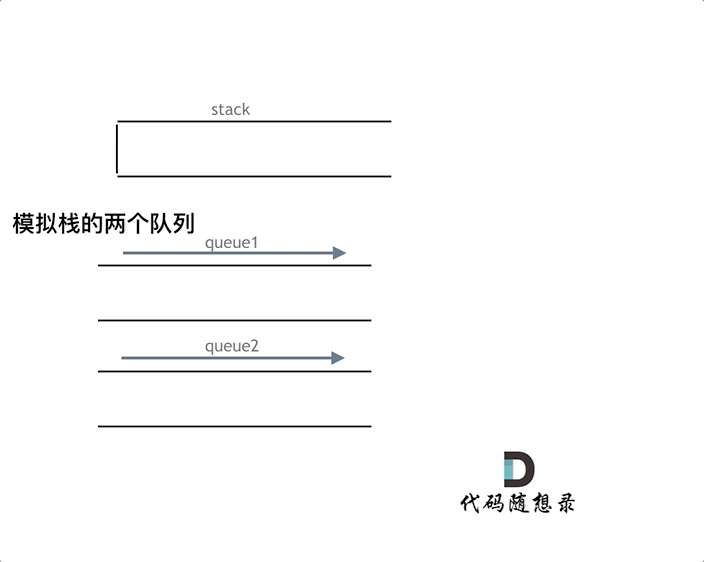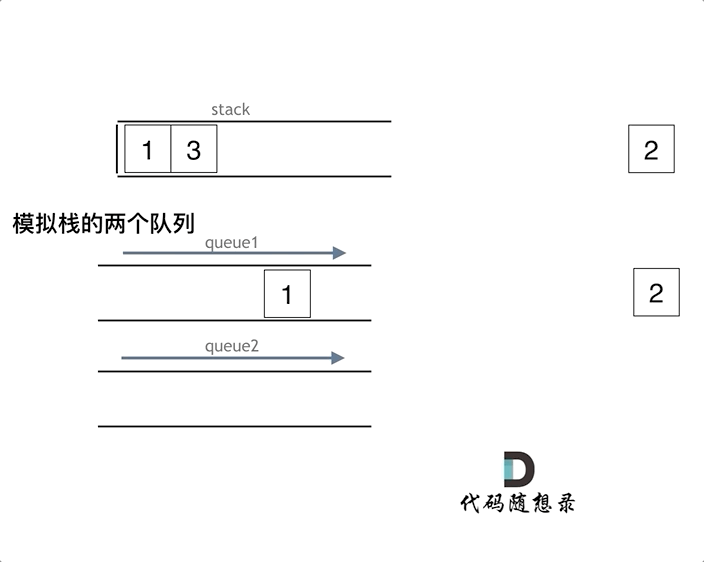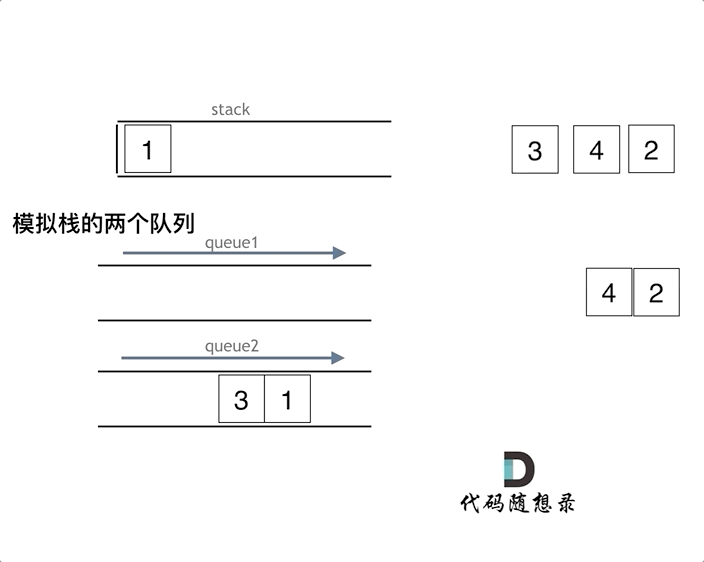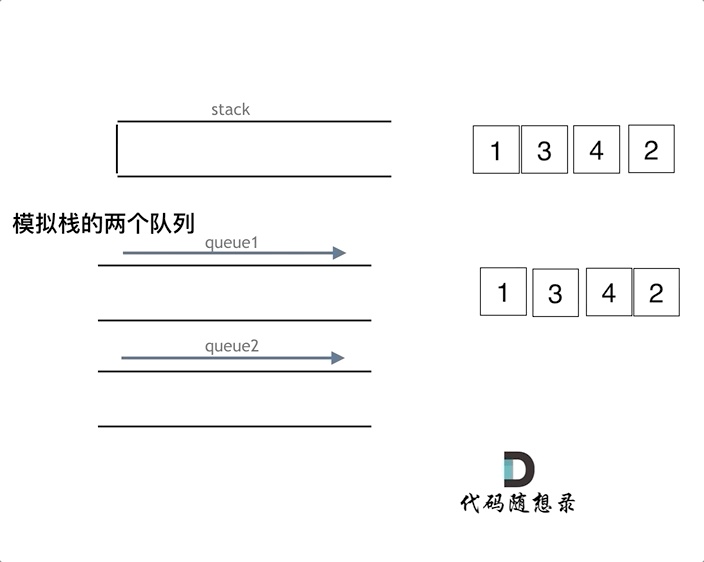
用两个队列实现栈
- 与上面的栈实现队列不同,用队列实现栈不能定义输入和输出队列,因为两个队列之间的数据传导,并没有改变输入输出的顺序
- 因此两个队列实现栈,是利用另一个队列临时存放数据,主队列pop到仅剩一个元素的时候,再pop就相当于pop栈顶元素了,而主队列之前pop的元素全部在另一个队列中临时存放,此时再把数据移回去就可以了
class MyStack {
public:
queue<int> que1;
queue<int> que2; // 辅助队列,用来备份
/** Initialize your data structure here. */
MyStack() {
}
/** Push element x onto stack. */
void push(int x) {
que1.push(x);
}
/** Removes the element on top of the stack and returns that element. */
int pop() {
int size = que1.size();
size--;
while (size--) { // 将que1 导入que2,但要留下最后一个元素
que2.push(que1.front());
que1.pop();
}
int result = que1.front(); // 留下的最后一个元素就是要返回的值
que1.pop();
que1 = que2; // 再将que2赋值给que1
while (!que2.empty()) { // 清空que2
que2.pop();
}
return result;
}
/** Get the top element. */
int top() {
return que1.back();
}
/** Returns whether the stack is empty. */
bool empty() {
return que1.empty();
}
};
- 时间复杂度: pop为O(n),其他为O(1)
- 空间复杂度: O(n)
只用一个队列实现:
- 只用一个队列实现,一个队列在模拟栈弹出元素的时候只要将队列头部的元素(除了最后一个元素外) 重新添加到队列尾部,此时再去弹出元素就是栈的顺序了。
class MyStack {
public:
queue<int> que;
/** Initialize your data structure here. */
MyStack() {
}
/** Push element x onto stack. */
void push(int x) {
que.push(x);
}
/** Removes the element on top of the stack and returns that element. */
int pop() {
int size = que.size();
size--;
while (size--) { // 将队列头部的元素(除了最后一个元素外) 重新添加到队列尾部
que.push(que.front());
que.pop();
}
int result = que.front(); // 此时弹出的元素顺序就是栈的顺序了
que.pop();
return result;
}
/** Get the top element. */
int top() {
return que.back();
}
/** Returns whether the stack is empty. */
bool empty() {
return que.empty();
}
};
- 时间复杂度: pop为O(n),其他为O(1)
- 空间复杂度: O(n)
3.有效的括号
有效的括号
括号匹配是使用栈解决的经典问题
如果还记得编译原理的话,编译器在 词法分析的过程中处理括号、花括号等这个符号的逻辑,也是使用了栈这种数据结构。
再举个例子,linux系统中,cd这个进入目录的命令我们应该再熟悉不过了。
cd a/b/c/../../
这个命令最后进入a目录,系统是如何知道进入了a目录呢 ,这就是栈的应用
有三种不匹配的情况:
- 第一种情况,字符串里左方向的括号多余了 ,所以不匹配
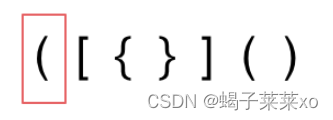
- 第二种情况,括号没有多余,但是 括号的类型没有匹配上

- 第三种情况,字符串里右方向的括号多余了,所以不匹配

- 因此需要一个栈,遍历字符串,在遇到左括号的时候,入栈,在遇到右括号的时候,判断当前的栈顶元素与右括号是否匹配,若匹配,就pop,继续遍历;若不匹配,就说明是无效括号;
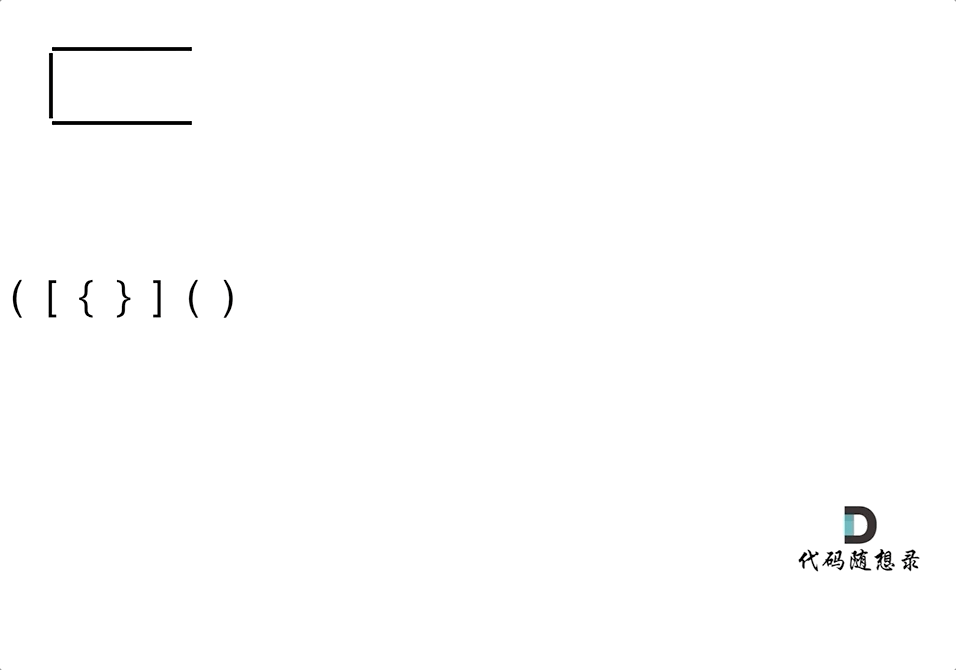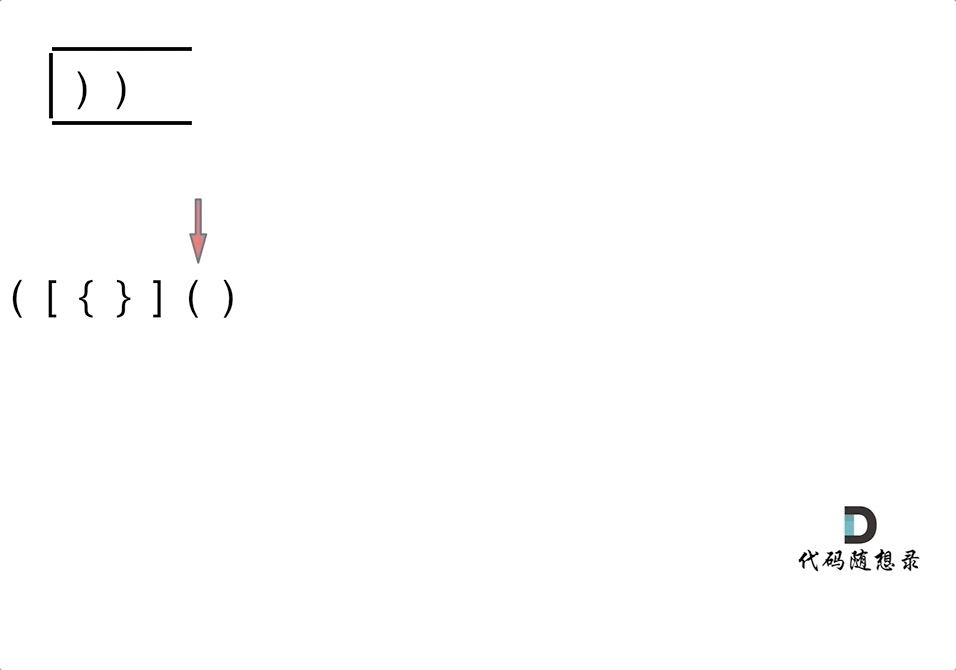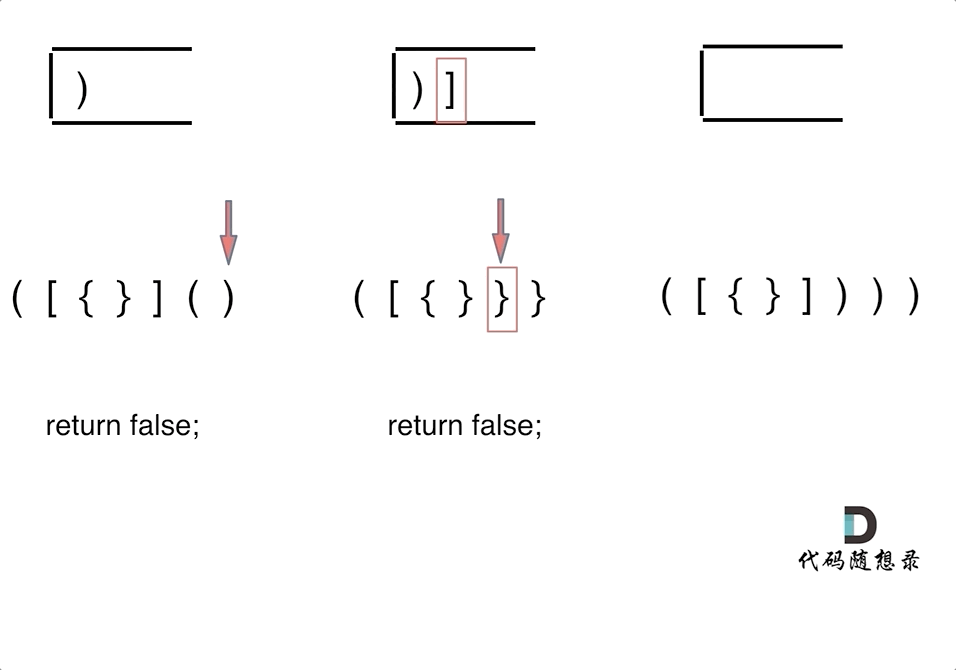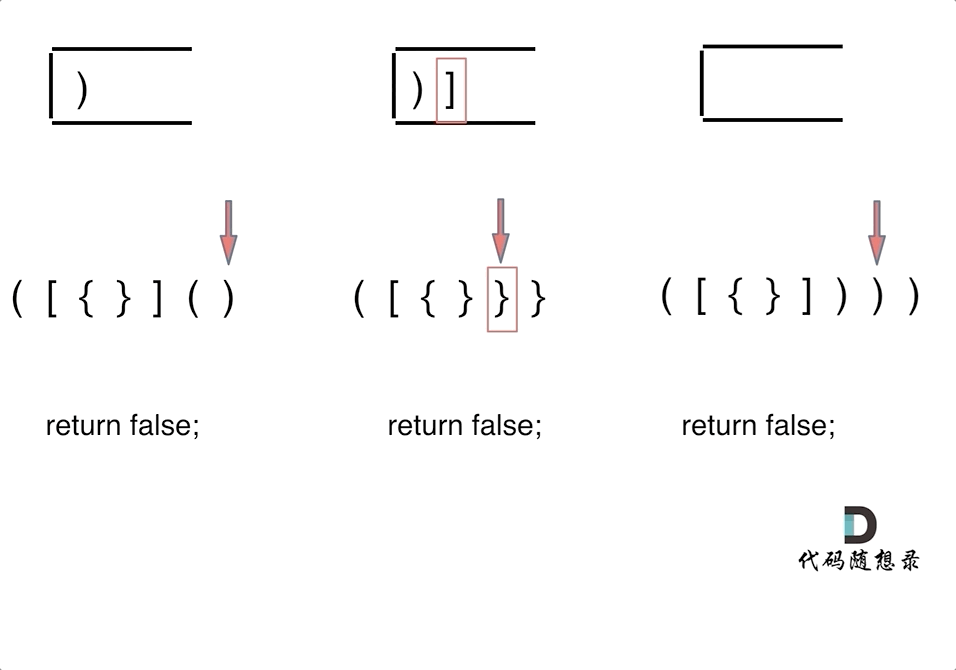
class Solution {
public:
bool isValid(string s) {
if (s.size() % 2 != 0) return false; // 如果s的长度为奇数,一定不符合要求
stack<char> st;
for (int i = 0; i < s.size(); i++) {
if (s[i] == '(') st.push(')');
else if (s[i] == '{') st.push('}');
else if (s[i] == '[') st.push(']');
// 第三种情况:遍历字符串匹配的过程中,栈已经为空了,没有匹配的字符了,说明右括号没有找到对应的左括号 return false
// 第二种情况:遍历字符串匹配的过程中,发现栈里没有我们要匹配的字符。所以return false
else if (st.empty() || st.top() != s[i]) return false;
else st.pop(); // st.top() 与 s[i]相等,栈弹出元素
}
// 第一种情况:此时我们已经遍历完了字符串,但是栈不为空,说明有相应的左括号没有右括号来匹配,所以return false,否则就return true
return st.empty();
}
};
- 时间复杂度: O(n)
- 空间复杂度: O(n)
4.前 K 个高频元素
- TopK问题,使用堆来做
- c++中的堆的实现是优先级队列priority_queue,默认建大队,可以使用仿函数自定义建堆规则
- 要求出现频率最高的k个元素,可以先用哈希表统计频率,再push到优先级队列中
- 这里我们根据频率的大小建小堆,小堆就是父节点一定不大于两个子节点,因此堆顶的就是堆中最小元素
- 我们将所有的元素入队,堆顶元素依次出栈,留下最后的k个元素就是频率最高的k的元素
class Solution {
public:
//仿函数控制建堆
class myComparison
{
public:
bool operator()(const pair<int, int>& left, const pair<int, int>& right)
{
return left.second > right.second;
}
};
vector<int> topKFrequent(vector<int>& nums, int k) {
vector<int> res(k);
unordered_map<int, int> cnt_map;
//统计每个整数的出现频率
for(const auto& n : nums)
{
cnt_map[n]++;
}
//建小堆
priority_queue<pair<int, int>, vector<pair<int, int>>, myComparison> pq;
// 固定优先级队列的大小为k,多出k的就将堆顶元素pop
for(auto it = cnt_map.begin(); it != cnt_map.end(); it++)
{
pq.push(*it);
if(pq.size() > k)
{
pq.pop();
}
}
//优先级队列中留下的k个数据就是前k个高频元素
for(int i = k - 1; i >= 0; i--)
{
res[i] = pq.top().first;
pq.pop();
}
return res;
}
};
文章来源:https://blog.csdn.net/kissland96166/article/details/135142159
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- mysql:1153 Got a packet bigger than ‘max_allowed_packet’ bytes的错误
- Linux环境docker安装RockerMQ(简单粗暴,复制即用)
- C++从零基础到入门(2)—— (if、switch、for、while语句)
- JavaOOP篇----第十篇
- Python中元祖的用法
- Apifox 最新更新:迭代分支功能上线、在线文档支持多格式导出!
- 第九节 初始化项目
- 手把手教你绘制和解读实用R列线图(Nomogram):从入门到精通
- 评论转换输出 - 华为OD统一考试
- 短视频矩阵系统:赋予用户创造与分享的力量