超详细 | 黏菌算法原理、实现及其改进与利用(Matlab/Python)
测试函数为F15
在MATLAB中执行程序结果如下:
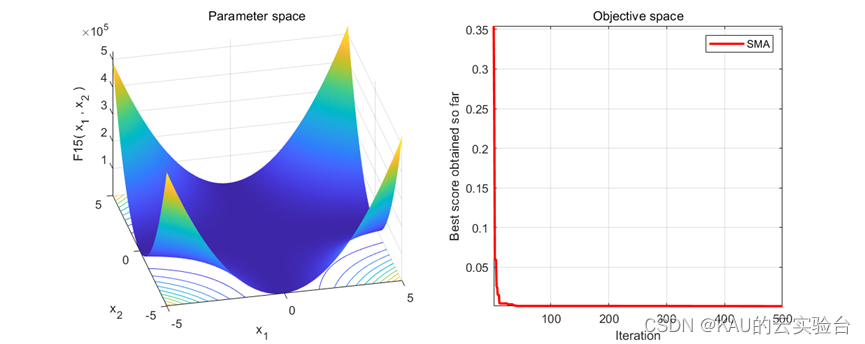
在Python中执行程序结果如下:
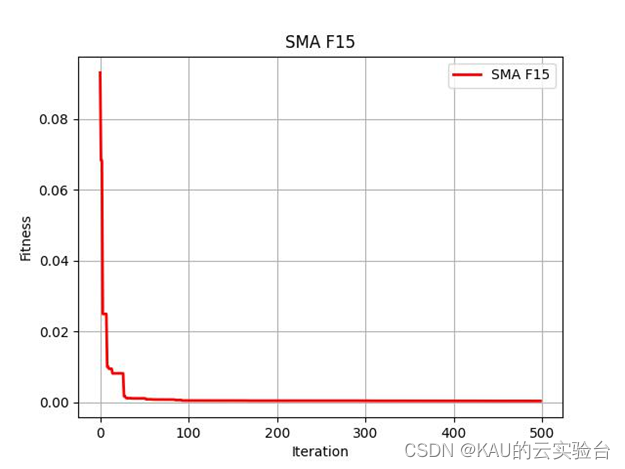
众所周知,麻雀搜索算法SSA是2020年由东华大学沈波教授团队提出[1]的一种性能十分优异的优化算法,而最近作者发现,在2020年还提出了一个优化算法,目前在谷歌学术和wos上引用量都高于SSA——黏菌算法(slime mould algorithm, SMA)
黏菌算法是由Li 等于 2020 年提出[2],发表在SCI的1区Top期刊《Future Generation Computer Systems》上,因此今天的文章作者就为大家介绍SMA,介绍其原理、优势及其可改进之处。
黏菌算法

麻雀搜索算法

00 目录
1 黏菌算法(SMA)原理
2 代码目录
3 算法性能
4 算法的改进与利用
5 源码获取
01 黏菌算法(SMA)原理
受文献[3]中的黏菌模型启发, Li等人[2]提出了名为黏菌算法(SMA)的基于群体智能实现的新型优化算法,该算法通过模拟黏菌的觅食过程来实现优化目的,具有参数少,寻优能力强的特点,目前也广泛应用于各类工程问题。
当黏菌感知到食物源时会表现出振荡收缩,而多食物源的出现还会使黏菌形成不同粗细的静脉网络,食物源的质量直接影响了静脉网络的状态。为探索更多的食物源,黏菌种群有一定概率进行未知领域的探索。黏菌觅食共表现出接近食物、包围食物和获取食物3个阶段。
1.1 接近食物
在第一阶段,黏菌依靠空气中的气味寻找食物来源,其位置更新公式为:
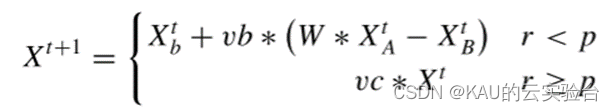
其中,r为在[0,1]的随机数,Xb表示目前适应度最优的个体位置,Xa与 Xb 为两个随机个体位置。vb和vc为振荡参数,vb 为 [-a,a] 之间的随机数,a=arctanh(1-t/Tmax),vb模拟黏菌种群中个体信息的交互过程,vc是从1到0线性递减的参数,c=1-t/Tmax,其模拟了黏菌对自身的保留。W 表示黏菌个体的权重因子,也是黏菌的质量,t 代表当前迭代次数,参数p为条件参数,用于控制黏菌位置更新方式,p=tanh|S(i)-DF|, Si为个体适应度值;DF为所有迭代中最优适应度值。
黏菌重量 W 的更新式为:

式中: Fcondition 为适应度排序的前 1/2 黏菌个体;Sindex为对种群适应度值大小进行排序;r2为分布于[0,1]的随机数,用于模拟静脉收缩模式的不确定性;bF、wF 为当前迭代最优、最差适应度值;log用于缓和数值的变化率使收缩频率数值变化较小。
黏菌种群根据食物的质量来调整自身搜索模式。当食物浓度较高时,该区域附近的重量W越大;当食物浓度较低时,区域的权重会降低,从而转向其他区域的探索。
1.2 包围食物
包围食物模拟了黏菌静脉结构在搜索过程中的收缩模式,在该步骤中,将黏菌的位置更新为
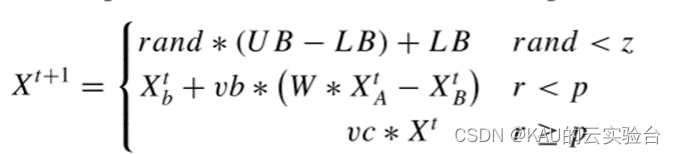
其中rand和r取区间[0,1]中的随机值,UB和LB分别是搜索范围的上边界和下边界。z是一个参数,为黏菌分离个体搜索其他食物源的概率,即产生变异的概率,一般设置其为 0.03。
1.3 获取食物
食物源的吸引会引起黏菌自身的振荡,进而改变静脉网络中细胞质的流动,使得黏菌不断靠近食物源,vb和vc即是模拟这种振荡的参数,vb的值在[?a,a]之间随机振荡,vc的值在[? 1,1]之间振荡,并随着迭代次数的增加逐渐趋于零。
黏菌位置更新的过程以及算法流程图可作出如下图示:
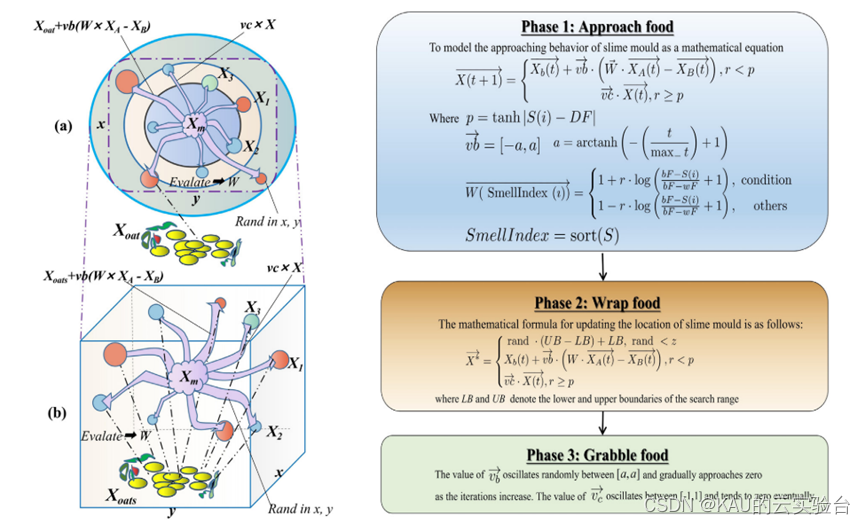
图 1 图来源于 Multi-parameter identi?cation of concrete dam using polynomial chaos expansion and slime mould algorithm
图表明,黏菌个体可以在没有任何角度或方向约束的情况下觅食。这使黏菌能够在所有可能的方向上接近最优解。
黏菌算法的核心更新机制就是下图中的式子,第一个式子保证了算法一定的随机性,而后两个式子随着震荡幅度的变化能够让算法分别进行全局和局部的搜索。
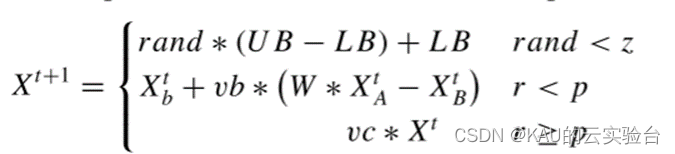
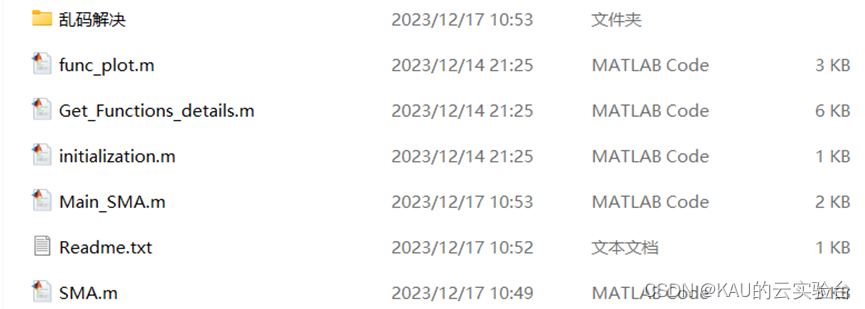
02 代码目录

代码包含MATLAB和Python,考虑到很多同学获取代码后,MATLAB代码部分有乱码(MATLAB版本问题),可以将MATLAB版本改为2020及以上,或使用乱码解决文件夹中的txt文件即可。
代码都经过作者重新注释,代码更清爽,可读性强。
部分代码:
MATLAB:
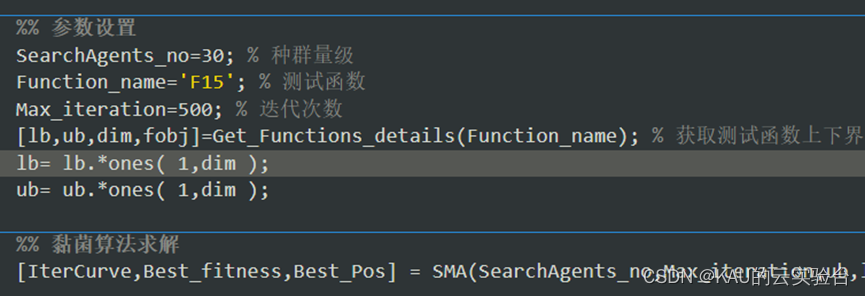
Python:
03 算法性能
采用标准测试函数初步检验其寻优性能
测试函数为F15
在MATLAB中执行程序结果如下:
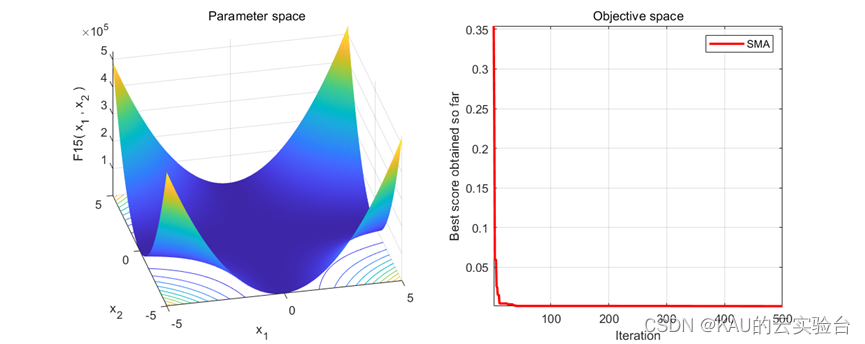
在Python中执行程序结果如下:
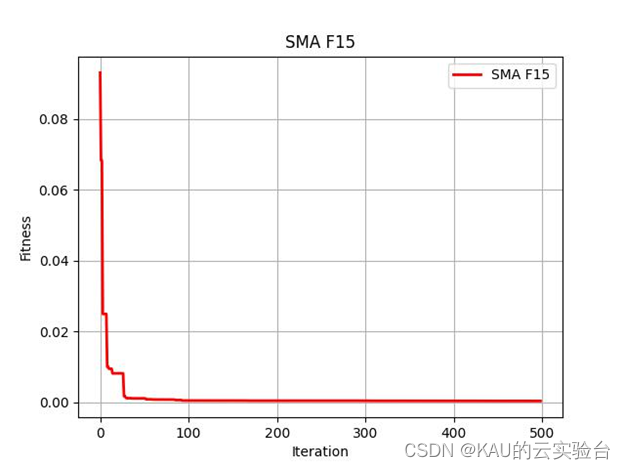
04 算法的改进与利用
根据没有免费的午餐(NFL)定理[4],没有一个算法可以处理所有的优化问题,即每个算法都有其优势和局限性,这也激励着学者提出各种改进的算法来解决不同类型的优化问题,同时也为算法间的混合利用提供了参考。这一节作者就简要谈一下SMA的可改进之处及其可利用的优点。
4.1 改进
首先,振荡参数vb和vc是SMA中相当重要的两个参数,其控制着算法的勘探和开发,而vb中的a在迭代中减小的极快,这可能会导致算法勘探与开发的不平衡,而vc中的c则是线性递减的变化策略,但SMA的实际优化过程十分复杂,其线性递减策略不能有效协调算法全局和局部搜索的平衡关系,会对算法寻优性能产生一定影响,因此两个振荡参数是可以进行改进的地方。
其次,尽管黏菌已经找到了更好的食物源,但对于优质黏菌来说,当rand<z时的黏菌流放可能会导致优质的黏菌个体损失,往更大的方面来说,黏菌算法并没有贪心策略,这虽然有利于解空间的探索,但可能导致算法收敛慢。
?最后,随着离食物源距离的靠近,振荡策略在后期影响力很小,削弱了算法跳出局部最优的能力。
4.2 利用
SMA 会根据适应度值调整不同的搜索模式,适应度较差的黏菌进行全局搜索,vb 和 vc的振荡也使黏菌的搜索方向更为发散,同时当rand小于 z 时,黏菌会进行随机初始化。因此,SMA 的多重探索机制使该算法具有强大的全局寻优能力。可以引入其他算法以提高其全局寻优能力。
05 源码获取
在GZH(KAU的云实验台)后台回复 SMA 即可
参考文献
[1] XUE J K, ShEN B. A novel swarm intelligence optimization approach: sparrow search algorithm [J]. Systems Science & Control Engineering, 2020, 8(1): 22-34.
[2] LI Shimin, CHEN Huiling, WANG Mingjing, et al. Slime mould algorithm: a new method for stochastic optimization[J]. Future generation computer systems, 2020, 111:
300–323.
[3] D. Monismith, B. Mayfield, Slime mold as a model for numerical optimization, in: 2008 IEEE Swarm Intelligence Symposium, 2008,pp. 1–8.
[4] Wolpert DH, Macready WG. No free lunch theorems for optimization. IEEE transactions on evolutionary computation 67–82, 1997.
另:如果有伙伴有待解决的优化问题(各种领域都可),可以发我,我会选择性的更新利用优化算法解决这些问题的文章。
如果这篇文章对你有帮助或启发,可以点击右下角的赞/在看(? ??_??)?(不点也行),你们的鼓励就是我坚持的动力!若有定制需求,可私信作者。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 如何实现一个好用的全链路多测试环境(HTTP篇)
- Git 使用规范:起名字、提交描述的最佳实践
- X11转发图形界面的问题处理方式 --- 页面图片,验证码不显示
- 【知识分享】Java实现“羊了个羊”的思路和代码
- 15:00面试,15:06就出来了,问的问题有点变态。。。
- 等保 2.0 三级 拓扑图+设备套餐+详解
- Json的书写
- 三款红外接收二极管电路图
- 一文掌握Java注解之@SpringBootApplication知识文集(1)
- Java中四种引用类型(强、软、弱、虚)