day22 二叉树part08
发布时间:2024年01月24日
235. 二叉搜索树的最近公共祖先
中等
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
二叉搜索树的迭代法很好用,比如找一个值
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
while (root != NULL) {
if (root->val > val) root = root->left;
else if (root->val < val) root = root->right;
else return root;
}
return NULL;
}
};
难点:当我们从上向下去递归遍历,第一次遇到 cur节点是数值在[q, p]区间中,那么cur就是 q和p的最近公共祖先。
// 迭代法
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
while (true) {
if (root.val > p.val && root.val > q.val) { // 当root在两节点右边时
root = root.left;
} else if (root.val < p.val && root.val < q.val) { // 当root在两节点左边时
root = root.right;
} else { // root.val 处于 p.val 和 root.val 之间
return root;
}
}
}
}
// 递归法
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root.val > p.val && root.val > q.val) return lowestCommonAncestor(root.left, p, q); // 当root在两节点右边时
if (root.val < p.val && root.val < q.val) return lowestCommonAncestor(root.right, p, q);// 当root在两节点左边时
return root; // root.val 处于 p.val 和 root.val 之间
}
}
701. 二叉搜索树中的插入操作
中等
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果
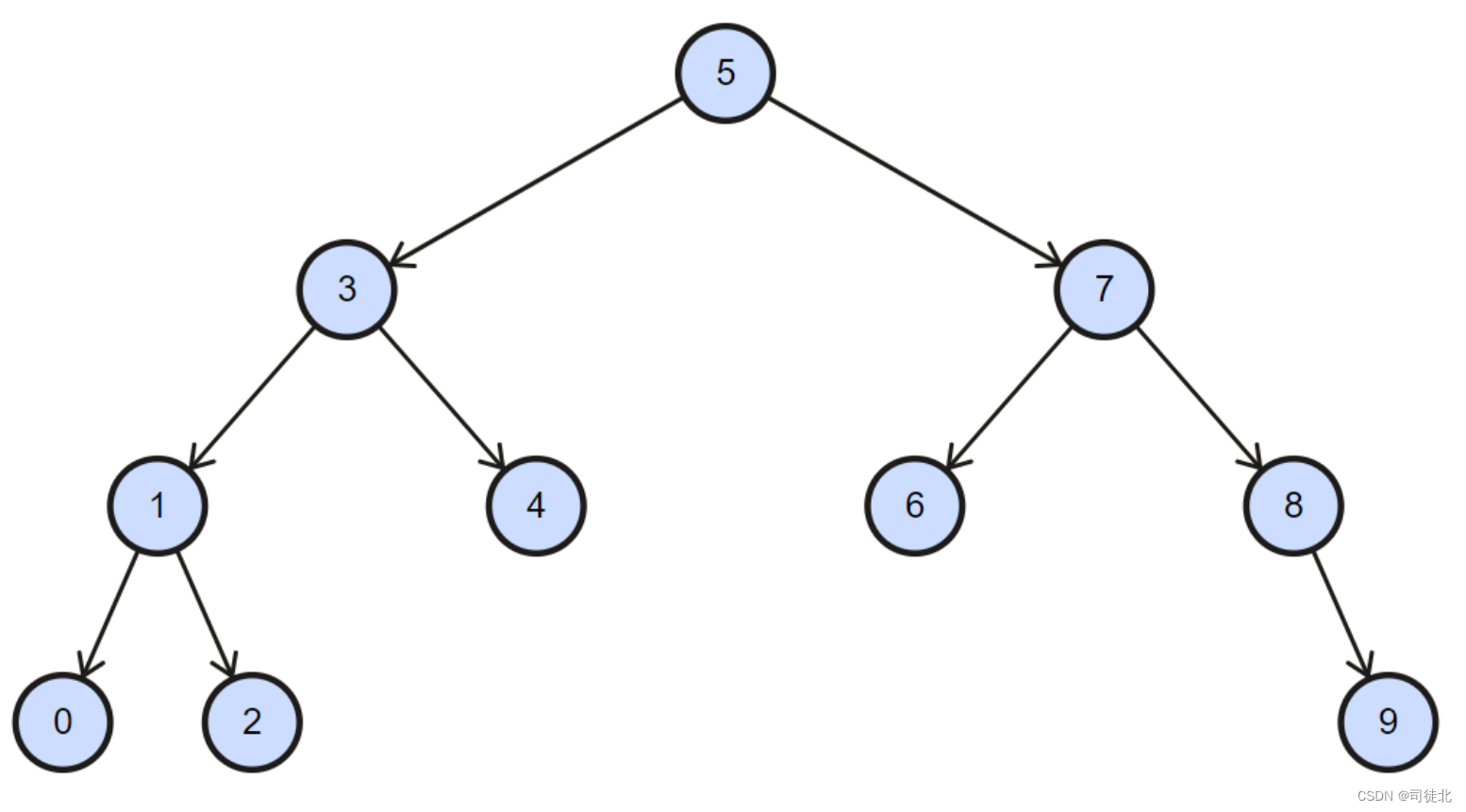
难点:为什么这样从上往下插入就可以满足二叉搜索树呢?首先回答我一个问题,假设你将要插入的这个数已经被正确插入了,那么你会怎样去找到它?你会发现你找他的顺序就是你插入的顺序。找到它和插入它用的逻辑是一样的。如果用这个某个规则找到了某个元素i,那么说明这个规则是满足二叉搜索树的,所以用这个规则来插入绝对也是满足二叉搜索树的。
假设在上图插入一个1.5,那么肯定选5这个节点的左边,注意,此时,就不用再管会不会大过5的右子树了,因为5的右子树肯定比5大,你都比5小了,就不用跟别人比了。然后和3比,发现没3大,此时往左走,那么3的右子树就不用想着可能比1.5小了。走到1,再往右走到2,此时左边界是1,右边界是2,就这样确定下来了。所以,为什么往下这样插入可以满足二叉搜索树?因为每经过一个节点都确定了一个边界。
// 迭代法
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
TreeNode node = new TreeNode(val); // 待插入节点
TreeNode cur = root;
TreeNode pre = root;
if (root == null) return node;
while (cur != null) {
pre = cur;
if (cur.val > val) {
cur = cur.left;
} else {
cur = cur.right;
}
}
if (pre.val > val) {
pre.left = node;
} else {
pre.right = node;
}
return root;
}
}
// 递归法,这个还是需要想一想的
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
if (root == null) return new TreeNode(val);
if (val < root.val) {
root.left = insertIntoBST(root.left, val);
} else {
root.right = insertIntoBST(root.right, val);
}
return root;
}
}
450. 删除二叉搜索树中的节点
中等
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
首先找到需要删除的节点;
如果找到了,删除它。
难点:要有先找后删的中心思想
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if (root == null) return null;
if (root.val == key) {
// 如果找到的这个节点是叶子节点或者只有左或者右节点
if (root.left == null) return root.right;
if (root.right == null) return root.left;
// 如果找到的这个节点下面挂着俩节点,那就交换它和右子树最大节点(或左子树最小节点)的位置
TreeNode minNode = getMin(root.right);
//在最小节点本来的位置删除这个最小节点
root.right = deleteNode(root.right, minNode.val); // 这里是通过赋值的方式来删除的,,不是你传进去一个节点就能删了,所以别忘了root.right= ... 这里一定要把删除后的子树接住
// 用右子树最小的节点替换 root 节点
minNode.left = root.left;
minNode.right = root.right;
root = minNode;
} else if (root.val > key) {
root.left = deleteNode(root.left, key); // 这里老是忘记写 root.left =
} else if (root.val < key) {
root.right = deleteNode(root.right, key);
}
return root;
}
public TreeNode getMin(TreeNode node) {
while (node.left != null) { // 一直往左找就能找到最小的
node = node.left;
}
return node;
}
}
以下内容来自:https://labuladong.github.io/algo/
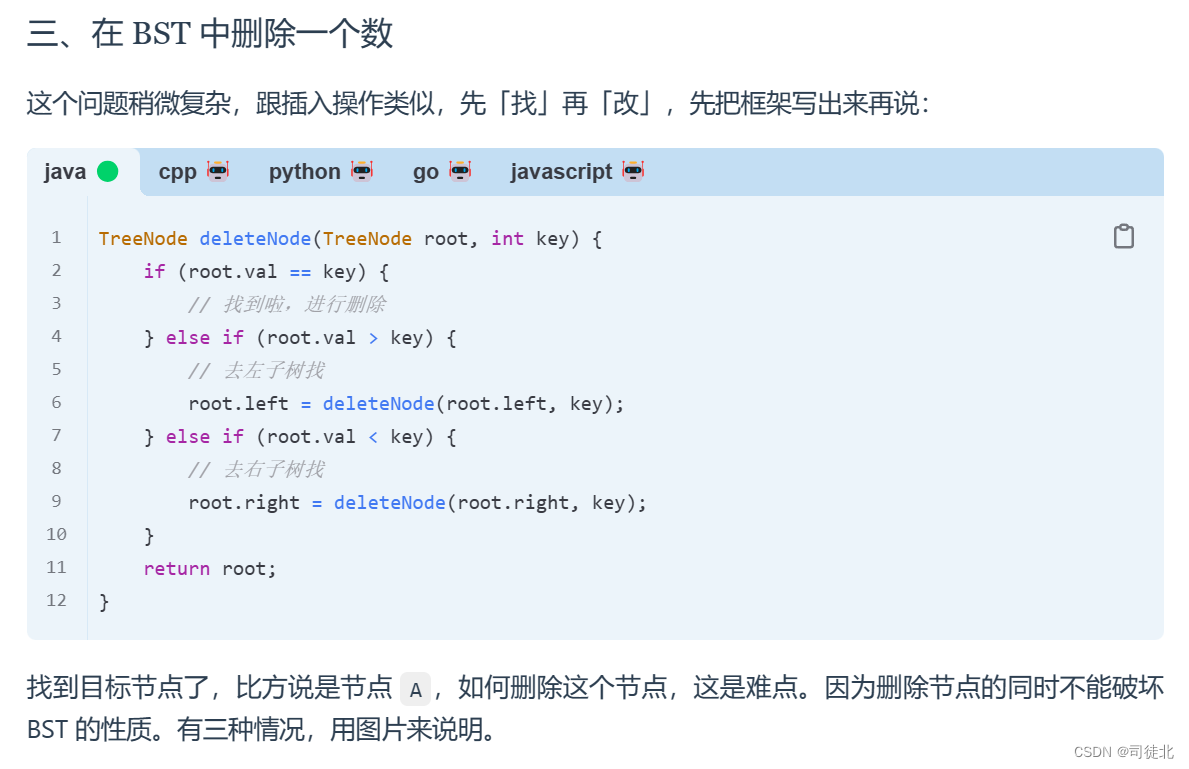
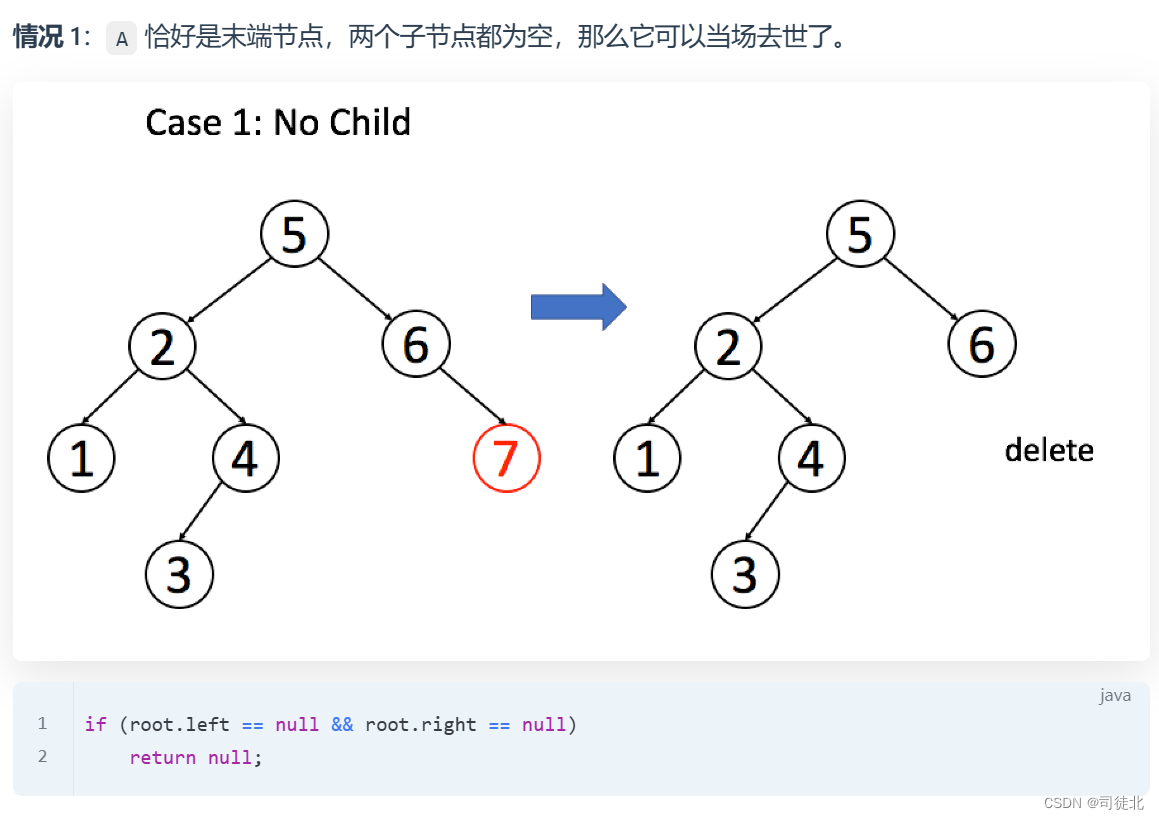
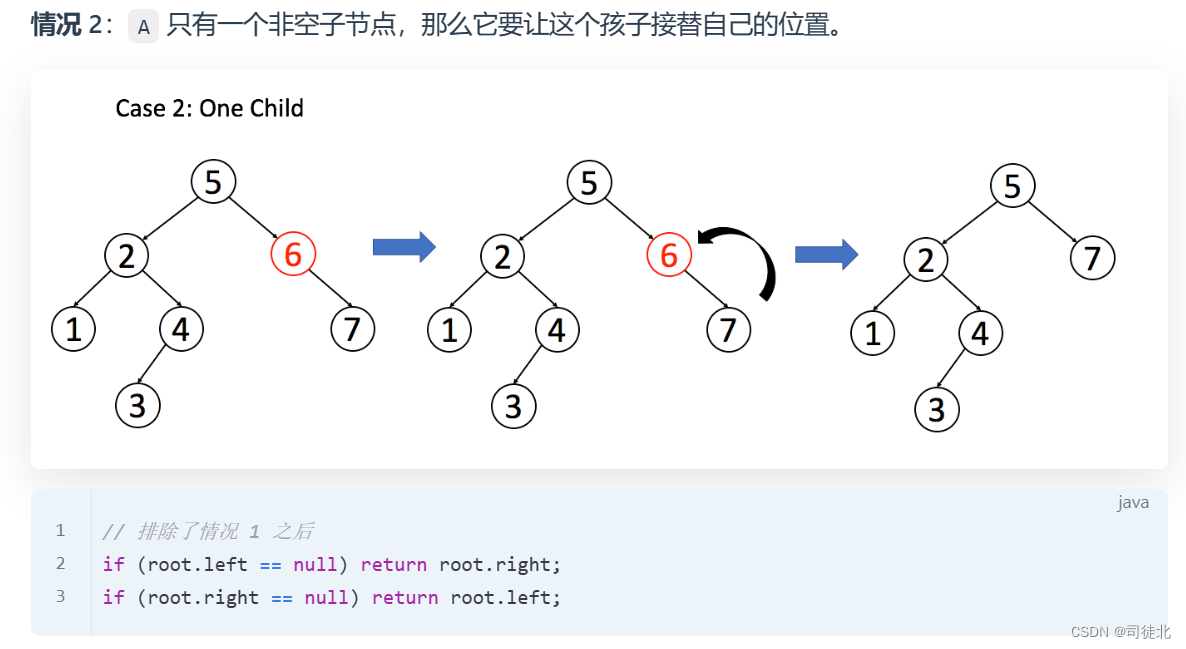
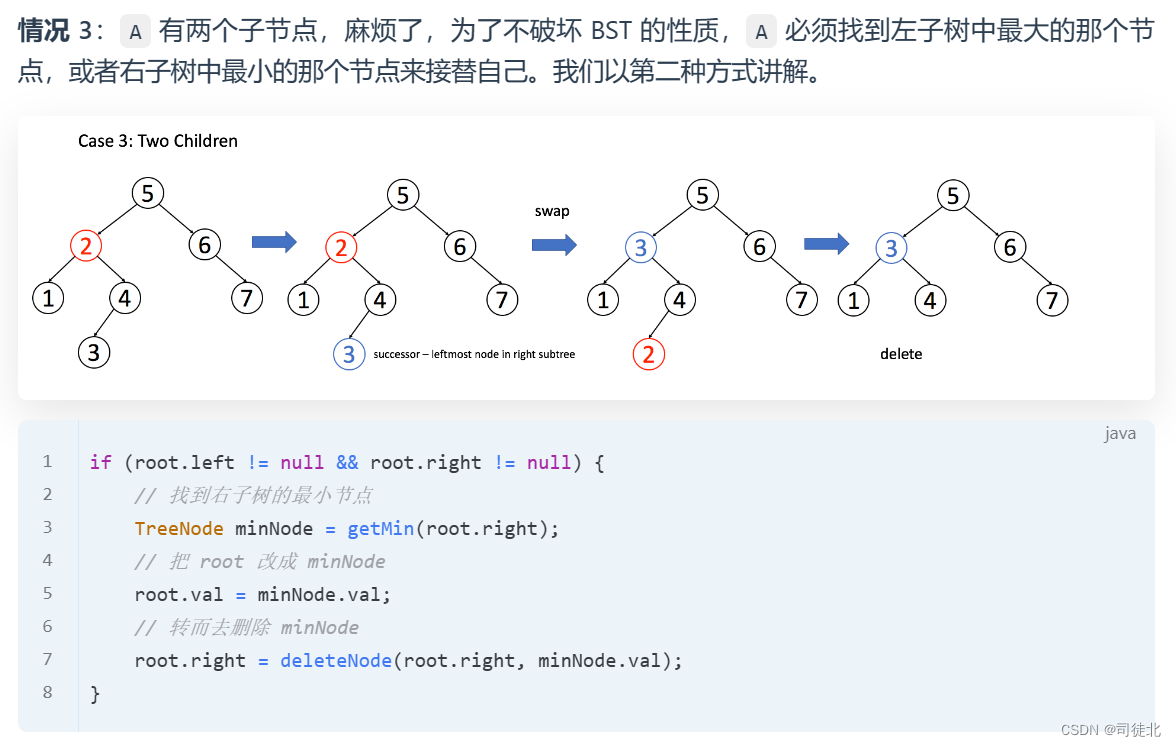
// labuladong代码
TreeNode deleteNode(TreeNode root, int key) {
if (root == null) return null;
if (root.val == key) {
// 这两个 if 把情况 1 和 2 都正确处理了
if (root.left == null) return root.right;
if (root.right == null) return root.left;
// 处理情况 3
// 获得右子树最小的节点
TreeNode minNode = getMin(root.right);
// 删除右子树最小的节点
root.right = deleteNode(root.right, minNode.val);
// 用右子树最小的节点替换 root 节点
minNode.left = root.left;
minNode.right = root.right;
root = minNode;
} else if (root.val > key) {
root.left = deleteNode(root.left, key);
} else if (root.val < key) {
root.right = deleteNode(root.right, key);
}
return root;
}
TreeNode getMin(TreeNode node) {
// BST 最左边的就是最小的
while (node.left != null) node = node.left;
return node;
}
文章来源:https://blog.csdn.net/weixin_43889767/article/details/135759016
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 模拟电路基础知识经典 200问,收藏这些就够了!
- TS 36.211 V12.0.0-上行(6)-PRACH
- Preview Django Templates
- python组合数据类型
- java生产设备效率管理系统Myeclipse开发mysql数据库web结构java编程计算机网页项目
- python高级练习题库实验2(B)部分
- Docker进阶篇-安装MySQL主从复制
- CDN内容分发网络
- 专访 | STIF2023第四届国际科创节访第七在线CEO赵嘉程
- 无监督学习 - 高斯混合模型(Gaussian Mixture Model,GMM)