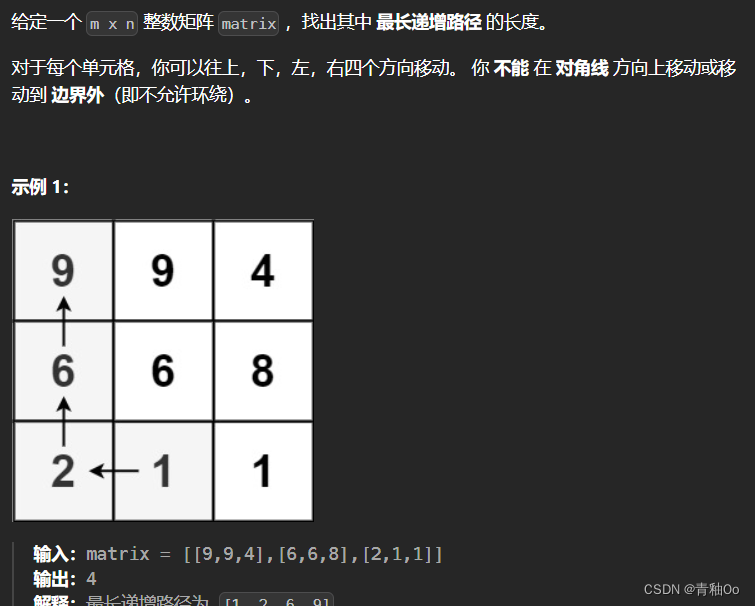
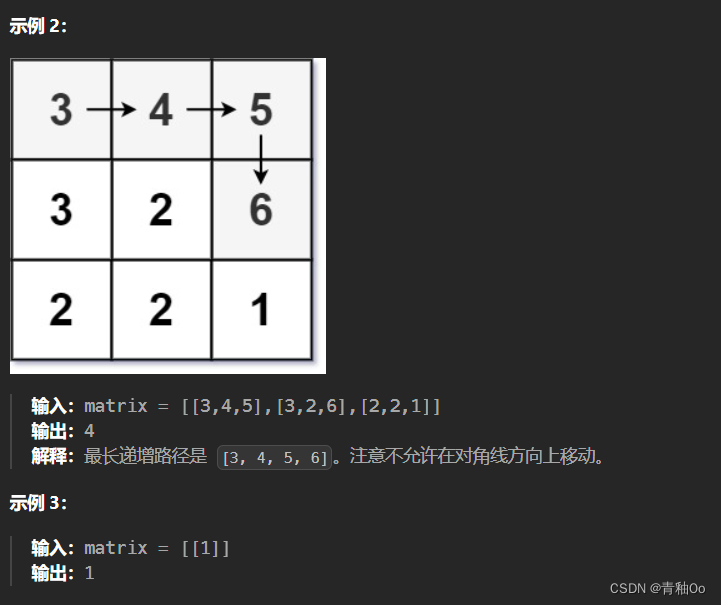
矩阵中的最长递增路径
发布时间:2024年01月09日
题目链接
题目描述
注意点
- 不能 在 对角线 方向上移动或移动到 边界外(即不允许环绕)
解答思路
- 因为最长递增路径一定是连续的,所以想到使用深度优先遍历来做。如果只使用深度优先遍历会导致超时(同一个节点的最长递增路径可能会计算多次),所以考虑引入动态规划存储每个节点的最长递增路径。除此之外,还要进行剪枝,主要是解决边界问题和移动后的值小于当前值的情况
代码
class Solution {
int row;
int col;
int[][] directions;
public int longestIncreasingPath(int[][] matrix) {
int res = 0;
row = matrix.length;
col = matrix[0].length;
directions = new int[][] {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
int[][] dp = new int[row][col];
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
res = Math.max(res, findMaxPath(matrix, dp, i, j));
}
}
return res;
}
public int findMaxPath(int[][] matrix, int[][] dp, int i, int j) {
if (dp[i][j] != 0) {
return dp[i][j];
}
int maxPath = 0;
for (int[] direction : directions) {
int x = i + direction[0];
int y = j + direction[1];
if (x < 0 || x >= row || y < 0 || y >= col) {
continue;
}
if (matrix[x][y] <= matrix[i][j]) {
continue;
}
maxPath = Math.max(maxPath, findMaxPath(matrix, dp, x, y));
}
dp[i][j] = maxPath + 1;
return dp[i][j];
}
}
关键点
- 深度优先遍历的思想
- 动态规划的思想
- 注意边界问题
文章来源:https://blog.csdn.net/weixin_51628158/article/details/135474909
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【python】基础知识类的语法功能讲解
- User Friendly大会 | 每日互动刘宇分享AIGC时代的数智营销变革
- 2023最受欢迎的20款黑客工具
- 使用 Docker 部署 Halo 博客系统
- 写给后端的Docker初级入门教程:基础篇
- leetcode第206题反转链表?
- Python 开发常用特性集锦--列表推导式、装饰器、列表和字典解包
- k8s pod基础 1
- 4.13 构建onnx结构模型-Conv
- 创新型产品说明书模板的设计与实践,我悟了!