Evidential Deep Learning to Quantify Classification Uncertainty

发布时间：2023年12月30日

本片文章发表于NeurIPS 2018。

一、概述

近年来，神经网络在不同领域取得了革命性的进步，尤其是在dropout、normalization以及skip connection等方法被提出之后，撼动了整个机器学习领域。在拥有足够的labelled data的条件下，训练一个拥有卓越性能的神经网络模型已经不再是一件稀奇的事情了，我们或许应该将目光转移到模型的鲁棒性、样本效率、安全性和可解释性等其他方面上。

比如，假设我们在MNIST数据集上训练得到了一个几乎有100%准确率的神经网络，当我们输入一张 “猫”的图片的时候，它是否能够给出正确的预测结果呢？对于经典的神经网络，即，参数确定的神经网络（deterministic neural networks），答案很显然是不能。因为我们的模型在训练时从未考虑过“猫”这个类别，在决策层也没有一个可以表示“猫”的输出单元。这是当前神经网络普遍存在的一个问题，即无法处理分布外（out of distribution, OOD）的数据。

然而这并不是最糟的，因为我们会发现即使我们输入了一张“猫”的图片，神经网络仍然会输出“0-9”之间的一个类别，比如，把“猫”预测为数字“0”。这种现象的发生是因为deterministic neural networks并不具备描述“I don't know”的能力，即使这个能力看起来十分基本而简单。基于此，贝叶斯神经网络将网络参数视为随机变量（服从一个特定分布）而不是一个确定的值，通过近似后验分布的矩（比如均值、方差）来估计预测的uncertainty。一旦有了uncertainty，就可以据此对预测结果进行评判，提醒用户谨慎对待那些uncertainty较大的样本。

本文从theory of evidence的角度切入，同样将关注点聚焦于分类问题的uncertainty estimation问题上。作者将分类网络的标准输出softmax视为categorical distribution的参数集，并用Dirichlet density的参数来替换这个参数集——网络输出的类别预测结果是从Dirichlet density中采样得到的（有思想与贝叶斯网络很类似）。通过这种方式，模型的预测结果将服从一个分布，而不是一个点估计（作者在原文中将这个Dirichlet density视为“生产”这些点估计的“工厂”）。

实验证明，本文提出的方法在不确定性估计方面领先于最先进的贝叶斯神经网络模型。

二、方法

1. Deficiencies of Modeling Class Probabilities with Softmax

在输出层使用softmax函数将连续的activations映射为class probabilities几乎是所有深度神经网络的“金标准”。最终得到的模型可以被视为一个多项分布（给定输入，得到一个对应的多项分布），而这个分布的参数，也就是离散的类别概率，是由神经网络的输出所决定的。

对于一个? $K$ -class 的分类问题，the likelihood function for an observed tuple? $(\mathbf{x, y})$ ?is

$Pr(y|\mathbf{x},\theta)=\mathrm{Mult}(y|\sigma(f_1(\mathbf{x},\theta)),...\sigma(f_K(\mathbf{x},\theta)))$

其中? $\mathrm{Mult}$ ?是一个multinomial mass function； $f_j(\mathbf{x},\theta)$ ?是模型 $f(\cdot )$ ?的第? $j$ ?个输出，模型的参数为? $\theta$ ； $\sigma(u_j)=e^{u_j}/\sum _{i=1}^Ke^{u_K}$ ?是softmax function。

softmax负责将神经网络得到的关于类别预测的activations压缩到一个simplex内，使其满足概率的定义（非负、和为一）。通过优化参数? $\theta$ ?来最大化multinomial likelihood，等价于最小化对数似然 $-\mathrm{log}p(y|\mathbf{x},\theta)=-\mathrm{log}\sigma(f_y(\mathbf{x},\theta))$ ，也被称为交叉熵损失(cross-entropy loss)。

Cross-entropy loss的概率解释是极大似然估计MLE，但作为频率派的一种方法，MLE无法推断预测分布的方差。此外，?softmax 函数将神经网络输出进行指数运算而导致预测类别的概率被放大——这导致了一个问题，就是预测类别之间除了可以比较概率值的大小之外，它们之间的距离对不确定性估计没有任何价值。

上图是利用softmax做预测的例子，场景是手写数字“1”的旋转对应网络输出类别的变化。可以发现随着旋转角度的变化，左侧网络的预测类别会由“1”→“2”→“5”→“1”，并且即使预测错误其置信度也很高；右侧则输出了uncertainty，表示对预测结果的不确定。

2. Uncertainty and the Theory of Evidence

“The Dempster-Shafer Theory of Evidence (DST) is a generalization of the Bayesian theory to subjective probabilities.” ——D-S证据理论是贝叶斯理论的一种推广，使其更加适用于处理主观概率和不确定性的情况。关于D-S证据理论，本文只给出一些基本概念和重要公式（毕竟我也只懂个皮毛而已），更多的细节请查阅文献[1]。

D-S证据理论有以下几个特点：1. 不必满足概率可加性；2. 具有表达“不确定”和“不知道”的能力，这些信息由mass函数所表示，并且在证据合成过程中保留了这些信息；3. 允许将置信度赋予给假设空间的子集(不局限于单个元素)。这里提到的一些词可能大家会有些陌生，如mass函数、证据合成、假设空间，接下来我会解释一下D-S证据理论中涉及的一些基本概念和定义。

(1)?基本概念

设? $\Theta$ ?是一个“识别框架”(frame of discernment)，或称为“假设空间”；

(i) 基本概率分配 (Basic Probability Assignment, BPA)

在识别框架? $\Theta$ ?上的BPA是一个? $2^\Theta \rightarrow [0,1]$ ?的函数m，称为mass函数。m接受来自于识别框架 $\Theta$ ?所构成的幂集的输入，并将其映射到闭区间 [0, 1] 内的实数，用以表示某种“置信度”或“信任度”。并且满足：

$m(\varnothing )=0,\sum \limits_{A\subseteq \Theta}m(A)=1$

其中，使? $m(A)>0$ ?的? $A$ ?称为焦元(focal elements)。

(ii) 信任函数 (belief function)

在识别框架? $\Theta$ ?基于BPA的信任函数定义为：

$Bel(A)=\sum\limits_{B\subseteq A}m(B)$

即，A的所有子集的mass值之和。

(iii) 似然函数 (plausibility function)

在识别框架? $\Theta$ ?基于BPA的似然函数定义为：

$Pl(A)=\sum\limits_{B\cap A\neq \varnothing}m(B)$

即，所有与A交集不为空的集合的mass值之和。

(iv) 信任区间

在证据理论中，对于识别框架 $\Theta$ ?中的某个假设A，基于BPA的信任函数? $Bel(A)$ ?和似然函数 $Pl(A)$ ?构成了信任区间? $[Bel(A),Pl(A)]$ ，用以表示对某个假设的置信程度。

(2) Dempster合成规则

Dempster合成规则也称为证据合成公式，是Bayes公式的广义化。对于 $\forall A\subseteq\Theta$ ， $\Theta$ ?上的两个mass函数? $m_1,m_2$ ?的Dempster合成规则为：

$(m_1\oplus m_2)(A)=\frac{1}{K} \sum\limits_{B\cap C=A}m_1(B)\cdot m_2(C)$

其中， $K$ ?为归一化常数：

$K=\sum\limits_{B\cap C \neq\varnothing}m_1(B)\cdot m_2(C)$

对于有限个mass函数? $m_1,m_2,...,m_n$ ?的Dempster合成规则为：

$(m_1\oplus...\oplus m_n)(A)=\frac{1}{K} \sum\limits_{A_1\cap ...\cap A_n=A}m_1(A_1)\cdot...\cdot m_n(A_n)$

$K=\sum\limits_{A_1\cap ...\cap A_n\neq \varnothing}m_1(A_1)\cdot m_2(A_2)\cdot ...\cdot m_n(A_n)$

D-S证据理论将信任质量(belief mass)分配给识别框架的子集，比如样本可能的类别标签；也可以分配给整个框架本身，这时候表示真理可以是任何可能的状态，比如一个样本可能属于任何类别。而当将belief mass分配给整个识别框架的时候，就代表了“I don't know”。

主观逻辑 (Subjective Logic, SL)使用Dirichlet distribution形式化了DST辨识框架的信任分配，这使得SL能够利用证据理论的原理量化信任度和不确定性。具体来说，SL将辨识框架视为包含K个相互排斥的单元 (例如，类别标签)，并为每个单元? $k=1,...,K$ ?提供了一个信任质量belief mass?? $b_k$ ，并提供了一个整体的不确定性质量uncertainty mass? $u$ ?(就是分配给识别框架 $\Theta$ ?的belief mass)，共 $K+1$ ?个值。这K + 1个值非负，并且和为一：

$u+\sum \limits_{k=1}^Kb_k=1, where\ u\geq 0 \ and\ b_k \geq 0 \ for \ k=1,...,K$

单元 $k$ ?的信任度 $b_k$ 是根据该单元可用的证据evidence来计算的。设? $e_k\geq 0$ ?是第? $k$ ?个单元的evidence，那么belief mass与uncertainty mass通过以下式子计算：

$b_k=\frac{e_k}{S} \ and \ u=\frac{K}{S}$

其中? $S=\sum\limits_{i=1}^K(e_i+1)$ ，即所有证据之和再加上K；而uncertainty与总的evidence成反比，当没有evidence的时候，每个单元的belief mass将为0，此时? $S=K$ ，总体的uncertainty为1。

所谓的“证据”就是我们从数据中收集到的将样本分类为某一类别的“支持度量” (measure of the amount of support collected from data in favor of a sample to be classified into a certain class——有时候觉得用原文更好理解一点...)。而信任质量分配 (belief mass assignment)，也就是主观意见 (subjective opinion)，对应于参数为? $\alpha _k=e_k+1$ ?的Dirichlet distribution——也就是说，利用公式? $b_k=(\alpha_k-1)/S$ ?可以很容易地通过Dirichlet distribution的参数中得到subjective opinion? $b_k$ ?的值，其中? $S=\sum\limits_{i=1}^K\alpha_i$ ?被称为Dirichlet strength。

👆标准的神经网络的输出是对每个样本的可能类别进行“概率分配”，而基于evidence参数化的Dirichlet distribution表示的是这种“概率分配”的密度(density)，也就是说，它是对二阶概率和不确定性进行建模的。

👆Dirichlet distribution是概率质量函数(pmf)的可能值? $\textbf{p}$ ?的概率密度函数(pdf)，参数为 $\alpha\in \mathbb{R}^K$ 。公式中， $B(\boldsymbol{\alpha})$ ?is the K-dimensional multinomial beta function，确保概率密度函数的积分为1。

接下来举两个具体的例子：

(例1) 假设对于一个10-分类问题，我们有信任质量分配? $\mathbf{b}=\left \langle 0,...,0 \right \rangle$ ，这个时候先验分布是一个均匀分布，i.e.， $D(\mathbf{p}|\left \langle 1,...,1 \right \rangle)$ 。因为没有observed evidence，因此belief mass全部为0，由 $b_k=(\alpha_k-1)/S$ ?得到? $\alpha_k$ ?全部为1，此时? $u=1$ ；

(例2) 现在假设? $\mathbf{b}=\left \langle 0.8,...,0 \right \rangle$ （和可以不为1）；此时? $u=1-\sum \limits_{i=1}^Nb_k=0.2$ ，由? $u=\frac{K}{S}$ ?可得? $S=50$ ，再通过? $b_k=(\alpha_k-1)/S$ ?得到? $\alpha=\left \langle 41,1,...,1 \right \rangle$ ，即Dirichlet distribution的参数。

当我们给出opinion? $\mathbf{b}$ ?之后，进而求得? $\alpha$ ，则第? $k$ ?个单元的expected probability可以由Dirichlet distribution的均值给出： $\hat{p_k}=\frac{\alpha_k}{S}$ 。

当一个样本的观测值与K个属性其中之一相关联时，相应的Dirichlet参数会被更新/增加，更新整个分布。例如，图像中被检测到的某些pattern可能有助于将其分类到某一个特定的类别中。此时，对应于这个类别的Dirichlet参数应该增加；也就是说，在分类问题中Dirichlet distribution的参数可以体现每一个类别具有的evidence。

本文的作者认为神经网络能够通过Dirichlet distribution提供对样本进行分类的opinion。假设 $\boldsymbol{\alpha_i}=\left \langle \alpha_{i1},...,\alpha_{iK} \right \rangle$ ?是对于sample? $i$ ?的Dirichlet distribution参数，那么? $e_{i,j}=\alpha_{i,j}-1$ ?就是网络估计的样本? $i$ ?属于第? $j$ ?类的evidence。

3. Learning to Form Opinions

网络的输出层使用ReLU激活函数代替softmax以保证产生非负值(证据是非负的)，最后的输出结果将作为the evidence vector of predicted Dirichlet distribution.

具体来说，given a sample? $i$ ，let? $f(\mathbf{x}_i|\Theta )$ ?represent the predicted evidence vector， $\Theta$ ?是网络的参数，因此，最终的Dirichlet distribution的参数? $\boldsymbol{\alpha}_i=\mathbf{e}_i+1=f(\mathbf{x}_i|\Theta)+1$ ，这个分布的均值也就是 $\boldsymbol{\alpha}_i/S_i$ ?(recall $S_i=\sum\limits_{j=1}^K(\mathbf{e}_{i,j}+1)$ )可以表示为类别 $i$ ?的概率估计值。

Let $\mathbf{y}_i$ ?be a one-hot vector encoding the ground-truth class of observation $\mathbf{x}_i$ ?with $y_{ij}=1$ and $y_{ik}=0$ for all $k\neq j$ , and $\boldsymbol{\alpha}_i$ be the parameters of the Dirichlet density on the predictors. First, we can treat $D(\mathbf{p}_i|\boldsymbol{\alpha}_i)$ as a prior on the likelihood $\mathrm{Mult}(\mathbf{y}_i|\mathbf{p}_i)$ and obtain the negated logarithm of the marginal likelihood by integrating out the class probabilities.

(Note: marginal likelihood? $p(\mathbf{y}|\boldsymbol{\alpha})=\int p(\mathbf{y}|\mathbf{p})\cdot p(\mathbf{p}|\boldsymbol{\alpha})d\mathbf{p}$ ?)

损失函数1：

$\mathcal{L}_i(\Theta)\\=-\textrm{log}(\int \prod \limits_{j=1}^Kp_{ij}^{y_{ij}}\frac{1}{B(\boldsymbol{\alpha}_i)}\prod \limits_{j=1}^Kp_{ij}^{\alpha_{ij}-1}d\mathbf{p}_i)\\ =\sum \limits_{j=1}^Ky_{ij}(\textrm{log}(S_i)-\textrm{log}(\alpha_{ij}))$

优化? $\boldsymbol{\alpha}_i$ ?以最小化? $\mathcal{L}_i(\Theta)$ ?，这也被称为“Type II Maximum Likelihood”，对此我的理解就是最大边际似然。

我没有在网上搜到这个公式的完整推导过程，所以在这里写一下，不感兴趣的可以直接跳过以下部分：

$\mathcal{L}_i(\Theta)\\=-\textrm{log}(\int \prod \limits_{j=1}^Kp_{ij}^{y_{ij}}\frac{1}{B(\boldsymbol{\alpha}_i)}\prod \limits_{j=1}^Kp_{ij}^{\alpha_{ij}-1}d\mathbf{p}_i)\\ =-\textrm{log}\left [\frac{1}{B(\boldsymbol{\alpha}_i)} \int \prod \limits_{j=1}^K p_{ij}^{\alpha_{ij}+y_{ij}-1}d\mathbf{p}_i)\right ]\\ \\ \\= -\textrm{log}\left [ \frac{1}{B(\boldsymbol{\alpha}_i)}\cdot B(\boldsymbol{\alpha}_i+\mathbf{y}_i )\right ]\\ \\ \\= \textrm{log}\frac{B(\boldsymbol{\alpha}_i)}{B(\boldsymbol{\alpha}_i+\mathbf{y}_i )}\\ \\ B(\boldsymbol{\alpha}_i)=\frac{\prod \limits_{j=1}^K\Gamma (\alpha_{ij})}{\Gamma (\sum \limits_{j=1}^K\alpha_{ij})}=\frac{\prod \limits_{j=1}^K\Gamma (\alpha_{ij})}{\Gamma (S_i)} \\ \\ B(\boldsymbol{\alpha}_i+\mathbf{y}_i)=\frac{\prod \limits_{j=1}^K\Gamma (\alpha_{ij}+y_{ij})}{\Gamma (\sum \limits_{j=1}^K\alpha_{ij}+y_{ij})}=\frac{\prod \limits_{j=1}^K\Gamma (\alpha_{ij}+y_{ij})}{\Gamma (S_i+1)}$

二者相除：

$\frac{B(\boldsymbol{\alpha}_i)}{B(\boldsymbol{\alpha}_i+\mathbf{y}_i)}=\frac{\Gamma (S_i+1)}{\Gamma S_i}\prod \limits_{j=1}^K\frac{\Gamma(\alpha_{ij})}{\Gamma(\alpha_{ij}+1)} =\prod \limits_{j=1}^K\frac{S_i}{\alpha_{ij}}=\prod \limits_{j=1}^K(\frac{S_i}{\alpha_{ij} })^{y_{ij}}$

则有

$\mathcal{L}_i(\Theta)=\textrm{log}\frac{B(\boldsymbol{\alpha}_i)}{B(\boldsymbol{\alpha}_i+\mathbf{y}_i )}=\sum \limits_{j=1}^Ky_{ij}(\textrm{log}(S_i)-\textrm{log}(\alpha_{ij}))$

为了使? $\mathcal{L}_i(\Theta)$ ?最小，真实类别对应的? $\alpha_{ij}$ ?就要尽可能大，这意味着给正确的类分配更多的evidence/belief mass。

上述loss对应于PAC-learning中的Bayes classifier，而以下要介绍的是Gibbs classifier；

For the cross-entropy loss, the Bayes risk will read (损失函数2)：

$\mathcal{L}_i(\Theta)=\\\int \left [\sum \limits_{j=1}^K-y_{ij}\textrm{log}(p_{ij}) \right ] \frac{1}{B(\boldsymbol{\alpha}_i)}\prod \limits_{j=1}^Kp_{ij}^{\alpha_{ij}-1}d\mathbf{p}_i =\sum \limits_{j=1}^Ky_{ij}(\psi(S_i)-\psi (\alpha_{ij}))$

$\psi (\cdot )$ ?为digamma函数。

同样的方法也可以应用于误差平方和(损失函数3)：

$\mathcal{L}_i(\Theta)=\int \left \| \mathbf{y}_i-\mathbf{p}_i \right \|_2^2 \frac{1}{B(\boldsymbol{\alpha}_i)}\prod \limits_{j=1}^Kp_{ij}^{\alpha_{ij}-1}d\mathbf{p}_i \\=\sum \limits_{j=1}^K \mathbb{E}\left [ y_{ij}^2-2y_{ij}p_{ij}+p_{ij}^2 \right ] =\sum \limits_{j=1}^K(y_{ij}^2-2y_{ij}\mathbb{E}\left [ p_{ij} \right ]+\mathbb{E}\left [ p_{ij}^2 \right ] )$

在这三种损失函数中，作者使用了最后一种(误差平方和)，原因是实验发现其它两种会产生过高的belief mass并且性能不稳定，而对于这里面蕴含的理论研究留给未来工作。

关于最后一种损失的优点，贴一段原文：

👆损失函数可以被分解为一阶矩与二阶矩，最小化训练集中所有样本的prediction error和variance，并且优先考虑误差，方差其次。关于这一点，下面的Proposition给出了保证：

总而言之，根据损失函数3对网络进行优化，可以使一个样本的正确类别获得更多的证据，并去除其它类别的证据从而避免错误分类；此外，在预测误差较小的前提下，还可以减小方差(误差的优先级高于方差)。有关这几个命题的证明请参阅原论文的补充材料。

神经网络可能会为错误的标签生成一些证据。此时如果网络能正确分类样本——也就是说，对于正确类别的evidence高于其它类别的evidence——那么这些误导性的证据可能并不成问题；然而，对于无法正确分类的样本，我们希望总evidence趋向于零——也就是说，当网络对样本无法做出明确分类时，希望网络对所有可能类别的预测都趋于均匀（即不确定性较高），这个时候对应于：

$\boldsymbol{\alpha}_i=\left \langle 1,...,1 \right \rangle$ ? ? $u=1,S=K$

具体的实现方式是在损失函数中添加KL divergence作为惩罚项/正则项，使得除了“有利证据”之外的那些证据更接近于均匀分布，即，防止给某个错误类别分配多的evidence，其它错误类别分配少的evidence——既然都是错误的，那就均匀分配，用来表示“I don't know”。

$\mathcal{L}(\Theta)=\sum \limits_{i=1}^N\mathcal{L}_i(\Theta)+\lambda_t\sum \limits_{i=1}^NKL\left [ D(\mathbf{p_i|\tilde{\boldsymbol{\alpha_i}}}) \ ||\ D(\mathbf{p_i}|\left \langle 1,...,1 \right \rangle) \right ]$

where? $\lambda_t=\mathop{min}(1.0,t/10)\in[0,1]$ ?is the annealing coefficient,? $t$ ?is the index of the current training epoch.? $\tilde{\boldsymbol{\alpha_i}}=\mathbf{y}_i+(1-\mathbf{y}_i)\odot \boldsymbol{\alpha}_i$ ?is the Dirichlet?parameters after removal of the non-misleading evidence from predicted parameters αi for sample $i$ ?——? $\tilde{\boldsymbol{\alpha_i}}$ ?的第? $j$ ?维(正确类别所在的维度)是1，其它维是? $\boldsymbol{\alpha}_i$ ?原来的值(只惩罚misleading evidence)，并通过退火系数逐渐增加KL divergence对损失的影响。

三、实验及结果

Accuracy与其它方法comparable，这代表着对于uncertainty的扩展并不会影响模型精度；并且这个表格也不能完全说明问题，因为uncertainty=1的时候也当作是预测错误，但事实上这时候模型回答的是“I don't know”，而不是给出一个错误答案。

横坐标是阈值，代表超过此阈值的uncertainty对应的预测全部视为“I don't know”；纵坐标是accuracy。

左图：在MNIST训练集上训练模型，在notMNIST数据集上测试(该数据集包含字母而不是数字)；

右图：在CIFAR-10的前五个类别上训练，最后五个类别上测试。

在图中靠近右下角的曲线表现更好，表明在所有的预测中能给出最大的熵值。由图可见，EDL最优。

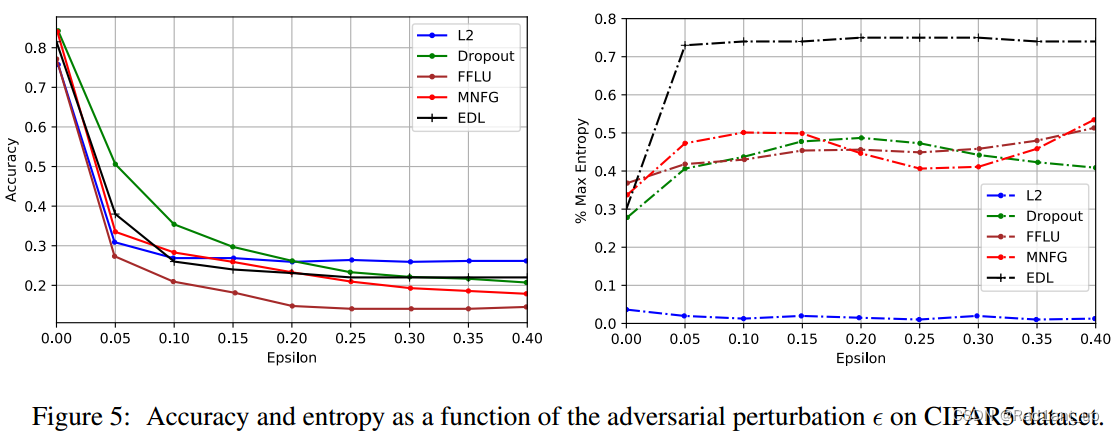
👆在对抗样本上的实验(MNIST and CIFAR-5)

Dropout对于对抗样本有最高的accuracy（左侧图）；然而它对所有预测都过于自信（右侧图）。也就是说，它对错误的预测同样给出了很高的置信度；除了EDL的其它模型也是类似的。

相反，EDL在uncertainty和准确率之间取得了很好的compromise。它对错误的预测赋予了非常高的uncertainty。

四、总结

作者从证据理论出发，假设类别的预测结果服从Dirichlet distribution，并使用神经网络输出“主观意见”，从而计算得到Dirichlet distribution的参数，最后使用得到的参数对预测类别及uncertainty进行估计；与标准神经网络使用softmax得到的点估计相比，额外提供了预测不确定性，使模型获得了描述“I don't know”的能力。

参考文献

Dempster, A. P. Generalization of Bayesian Inference. Journal of the Royal Statistical Society. Series B 30, 1968:205-247.

文章来源:https://blog.csdn.net/Rad1ant_up/article/details/135271212
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！