机器学习——特征选择（二）

【说明】文章内容来自《机器学习——基于sklearn》，用于学习记录。若有争议联系删除。

4、皮尔森相关系数

皮尔森（pearson）相关系数度量两个变量之间的相关程度。

?是用两个连续变量x,y的协方差 除以x,y各自的标准差的乘积 。皮尔森相关系数的值为-1~1，其性质 如下：

• 时，表示两个变量为正相关；当时，表示两个变量为负相关。
• 时，表示两个变量为完全相关。
• 时，表示两个变量无相关关系。
• 时，表示两个变量存在一定程度的相关。越接近1，两个变量的线性相关越强；越接近0，表示两个变量的线性相关越弱。

????????对一般可按3级划分：为低度相关；为显著相关；为高度相关。

4.1 皮尔森计算示例

import math
def pearson(vector1, vector2):
    n = len(vector1)
    sum1 = sum(float(vector1[i]) for i in range(n))
    sum2 = sum(float(vector2[i]) for i in range(n))
    #平方求和
    sum1_pow = sum([pow(v, 2.0) for v in vector1])# pow(x, n) ，即计算 x 的 n 次幂函数
    sum2_pow = sum([pow(v, 2.0) for v in vector2])
    p_sum = sum(vector1[i] * vector2[i] for i in range(n))
    #分子为num，分母为den
    num = p_sum - (sum1 *sum2 / n)
    den = math.sqrt((sum1_pow - pow(sum1,2) / n) * (sum2_pow - pow(sum2,2) / n))
    if den == 0:
        return 0.0
    return num/den
if __name__ == '__main__':
    vector1 = [2,7,18,88,157,90,177,570]
    vector2 = [3,5,15,90,180,88,160,580]
    print(pearson(vector1,vector2))

【运行结果】

4.2 系数应用示例

scipy.state 模块提供了pearsonr函数，以计算皮尔森相关系数，语法如下：

pearsonr(x,y)

【参数说明】

• x：特征
• y：目标变量

示例：

from scipy.stats import pearsonr
from sklearn.datasets import load_iris
from sklearn.feature_selection import VarianceThreshold
import pandas as pd
import matplotlib.pyplot as plt
iris = load_iris()
data = pd.DataFrame(iris.data, columns = ['sepal length', 'sepal width', 'petal length', 'petal width'])
data_new = data.iloc[:, :4].values

transfer = VarianceThreshold(threshold = 0.5)
data_variance_value = transfer.fit_transform(data_new)#方差

#计算两个变量的相关系数
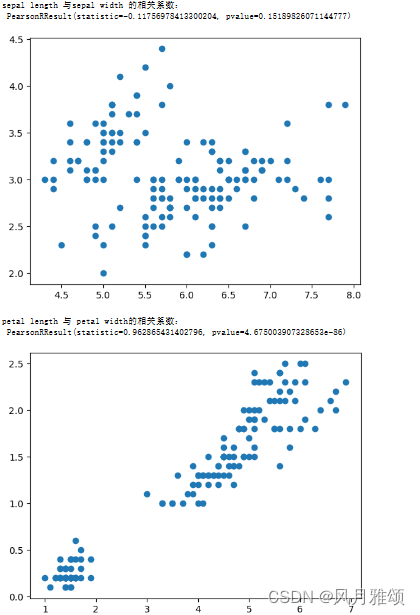
r1 = pearsonr(data['sepal length'], data['sepal width'])
print('sepal length 与sepal width 的相关系数：\n',r1)

plt.scatter(data['sepal length'], data['sepal width'])
plt.show()
r2 = pearsonr(data['petal length'], data['petal width'])
print('petal length 与 petal width的相关系数：\n', r2)
plt.scatter(data['petal length'],data['petal width'])
plt.show()

【运行结果】

5、嵌入法

????????嵌入法基于模型实现特征选择。基于模型的特征选择是使用有监督学习的模型对数据特征的重要性进行判断，保留最重要的特征，一般有基于惩罚项的特征选择和基于树模型的特征选择等方法。Sklearn提供了 SelectFromModel函数实现,其语法如下，

SelectFromModel(estimator, prefit=False)

【参数说明】

• estimator:评估器
• prefit:预设模型是否期望直接传递给构造函数。取值为bool值，默认为 False.5.8.1基于惩罚项的特征选择

5.1基于惩罚项的特征选择

????????采用惩罚项的模型进行特征选择，除了筛选出所需的特征外，同时进行降维处理。可以采用带有L1和L2惩罚项的逻辑回归模型进行特征选择，L1惩罚项保留多个对目标值具有同等相关性的特征中的一个，往往结合L2惩罚项进行优化。

示例：

from sklearn.svm import LinearSVC
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectFromModel
iris = load_iris()
X, y = iris.data, iris.target
print('X shape:',X.shape)
#使用线性支持向量机linearSVC模型进行特征选择，惩罚项为L1
lsvc = LinearSVC(C= 0.01, penalty = 'l1', dual = False).fit(X, y)
#C为正则化系数λ的倒数，必须为正数，默认为1。和SVM中的C一样，值越小，代表正则化越强。
#dual=False : 对偶或者原始方法。Dual只适用于正则化相为l2的‘liblinear’的情况，
#通常样本数大于特征数的情况下，默认为False。
model = SelectFromModel(lsvc, prefit = True)
X_new = model.transform(X)
print('X_new shape:',X_new.shape)

【运行结果】

5.2 基于树模型的特征选择

基于树的预测模型能够用来计算特征的重要程度，以去除不相关的特征。

示例：

from sklearn.ensemble import ExtraTreesClassifier#
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectFromModel
iris = load_iris()
X, y = iris.data, iris.target
print('X shape:', X.shape)
clf = ExtraTreesClassifier(n_estimators = 10)
clf = clf.fit(X, y)
print('feature_importance:', clf.feature_importances_)
model = SelectFromModel(clf, prefit = True)
X_new = model.transform(X)
print('X_new shape:', X_new.shape)

【运行结果】