基数（桶）排序

目录

基数排序

实现步骤

完整代码

---

基数排序

核心思想：统计原数组中某个元素在该数组中出现的次数

优点：效率极高，时间复杂度为O（aN + countN(范围)）?

缺点：不适合分散的数据，更适合集中数据；不适合浮点数、字符串、结构体类型的数据排序，只适合整数

实现步骤

1、先实现简单的统计原数组中某个元素在该数组中出现的次数

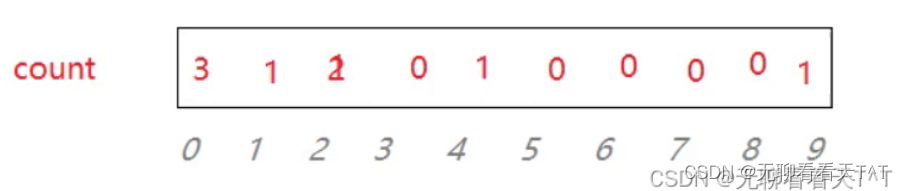
for(int i = 0;i<n;i++)
{
    count[a[i]]++;    //count数组用于统计个数、a数组表示原数组
}

?2、当数组元素过大时（比如1000，1998......），采用相对映射的办法解决不必要的循环（数组中的每一个数的值都应该大于或等于数组中最小的数的值，就拿下图的1000 1999 1888数组举例，min = 1000，a[0] - 1000 = 0，即count[0]++，表示1000在原数组中出现了一次且count[0]位置记录的是1000在原数组中出现的总次数，a[1] - 1000 = 999，表示1999在原数组中出现了一次且count[999]位置记录的是1999在原数组中出现的总次数......，这样做就可以实现原本count[1000]位置记录的是1000在原数组中出现的总次数变为了count[0]......，节省了很多空间）count数组下标表示由绝对映射转为相对映射的偏移量，在后面的排序过程中很重要（解释起来有点复杂建议自行理解，这里就不解释了，只引入了偏移量的改变便于理解）

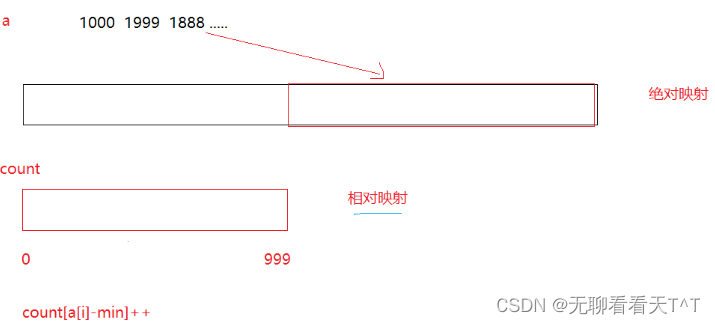
for (int i = 0; i < n; i++)
{
	count[a[i] - min]++;     //min是原数组中最小的数
}

3、求出原数组的最大值和最小值

int min = a[0], max = a[0];
for (int i = 1; i < n; i++)
{
	if (a[i] < min)
		min = a[i];

	if (a[i] > max)
		max = a[i];
}

4、 开辟临时数组

int range = max - min + 1;
int* count = (int*)calloc(range, sizeof(int));
if (count == NULL)
{
	printf("calloc fail\n");
	return;
}

calloc特点：为num个大小为size的元素开辟一块空间，并把空间的每个字节初始化为0?

calloc函数的详细使用方式：http://t.csdnimg.cn/bhOcS

5、 计数排序

后置--的特点是先返回后--

以上图所示的count数组为例子，for循环用于遍历整个计数数组，while循环用于将count数组中记录的原数组中出现次数非0的某元素的值依据它的出现次数多次逐位的赋值给原数组（count[0]位置记录的是原数组中1出现的次数3次，循环3--，每次循环都会将1这个数字不断地赋值到原数组中，即a[0] = 1、a[1] = 1、a[2] = 1）min表示起始值，j表示因为相对映射产生的偏移量，min+j表示相对映射前的真实值

int i = 0;
for (int j = 0; j < range; j++)
{
	while (count[j]--)
	{
		a[i++] = j + min;
	}
}

完整代码

// 基数排序/桶排序
void CountSort(int* a, int n)
{
	int min = a[0], max = a[0];
	for (int i = 1; i < n; i++)
	{
		if (a[i] < min)
			min = a[i];

		if (a[i] > max)
			max = a[i];
	}

	int range = max - min + 1;
	int* count = (int*)calloc(range, sizeof(int));
	if (count == NULL)
	{
		printf("calloc fail\n");
		return;
	}

	// 统计次数
	for (int i = 0; i < n; i++)
	{
		count[a[i] - min]++;
	}

	// 排序
	int i = 0;
	for (int j = 0; j < range; j++)
	{
		while (count[j]--)
		{
			a[i++] = j + min;
		}
	}
}

~over~