LLM 中的长文本问题
近期,随着大模型技术的发展,长文本问题逐渐成为热门且关键的问题,不妨简单梳理一下近期出现的典型的长文本模型:
-
10 月上旬,Moonshot AI 的 Kimi Chat 问世,这是首个支持 20 万汉字输入的智能助手产品;
-
10 月下旬,百川智能发布 Baichuan2-192K 长窗口大模型,相当于一次处理约35 万个汉字;
-
11 月上旬,OpenAI 发布支持 128K 上下文窗口的 GPT-4 Turbo 模型;
-
11 月下旬,Anthropic 发布支持 200K 上下文窗口的 Claude 2.1 模型;
-
12 月上旬,零一万物开源了长文本模型 Yi-6B-200K和 Yi-34B-200K。
实际上,随着文本长度的提高,模型能够处理问题的边界也大大提高,因此研究并解决长文本问题就显得非常必要。本文将从长文本问题的本质出发,逐步分析和研究长文本实现的问题及解决办法。
一、长文本的核心问题与解决方向
1.1 文本长度与显存及计算量之关系
要研究清楚长文本的问题,首先应该搞清楚文本长度在模型中的地位与影响。那么我们便以 Decoder-base 的模型为例来进行分析
1.1.1 模型参数量
Decoder-base 的模型主要包括 3 个部分:embedding, decoder-layer, head。
其中最主要部分是decoder-layer,其由 lll 个层组成,每个层又分为两部分:self-attention 和 MLP。
self-attention的模型参数有、、的权重矩阵 、、及bias,输出矩阵 及bias,4个权重矩阵的形状为 ( 表示 hidden_size),4个bias的形状为 。则 self- attention 的参数量为 。
MLP由2个线性层组成,一般地,第一个线性层是先将维度从 映射到 ,第二个线性层再将维度从映射到。第一个线性层的权重矩阵 的形状为 ,偏置的形状为 。第二个线性层权重矩阵 的形状为 ,偏置形状为 。则 MLP 的参数量为 。
self-attention 和MLP各有一个layer normalization,包含了2个可训练模型参数:缩放参数γ和平移参数β,形状都是。2个layer normalization的参数量为 。
由此,每个Decoder层的参数量为。
此外,embedding和head 的参数量相同,与词表相关,为(如果是 Tied embedding,则二者共用同一个参数)。由于位置编码多样,且参数量小,故忽略此部分。
综上, 层模型的可训练模型参数量为 。当 较大时,可以忽略一次项,模型参数量近似为。
1.1.2 计算量估计
如果说参数量是模型的固有属性,那么计算量便是由模型和输入共同决定,下面分析这一过程。假设输入数据的形状为 ( 表示batch_size,表示sequence_length)。
先分析Decoder中self-attention的计算量,计算公式如下:
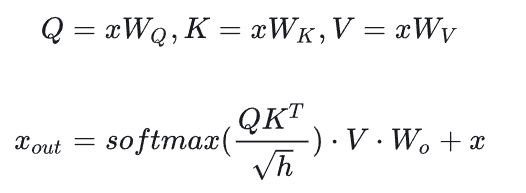
-
计算:矩阵乘法的输入和输出形状为。计算量为。
-
矩阵乘法的输入和输出形状为
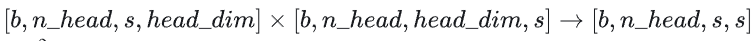
计算量为。
-
计算在上的加权,矩阵乘法的输入和输出形状为
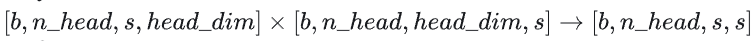
计算量为 。
-
attention后的线性映射,矩阵乘法的输入和输出形状为.计算量为。
接下来分析MLP块的计算,计算公式如下:
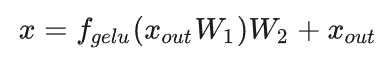
-
第一个线性层,矩阵乘法的输入和输出形状为 。计算量为 。
-
第二个线性层,矩阵乘法的输入和输出形状为 。计算量为。
将上述计算量相加,得到每个Decoder层的计算量大约为。
此外,另一个计算量的大头是logits的计算,将隐藏向量映射为词表大小。矩阵乘法的输入和输出形状为,计算量为。
因此,对于一个 lll 层的模型,输入数据形状为的情况下,一次前向计算的计算量为。
1.1.3 文本长度与计算量、参数量、显存的关系
忽略低次项,一次输入的tokens数为bs, 则计算量与参数量的关系为 在实际中通常 ,因此该项可近似认为约等于2。即在一次前向传递中,对于每个token,每个模型参数,需要进行2次浮点数运算(一次乘法法运算和一次加法运算)。考虑到后向传递的计算量是前向传递的2倍。因此一次训练迭代中,对于每个 token,每个模型参数,需要进行 次浮点数运算。
通过以上分析,我们可以得到结论:计算量主要和模型参数和 token 数相关,文本长度并不会显著增加计算量。那么这就引出另一个问题:文本长度与显存的关系。
除了模型参数、梯度、优化器状态外,占用显存的大头就是前向传递过程中计算得到的中间激活值。这里的激活(activations)指的是:前向传递过程中计算得到的,并在后向传递过程中需要用到的所有张量。
先分析 Decoder layer 中 self-attention 的中间激活:
-
对于 ,需要保存它们共同的输入 ,这就是中间激活。输入 的形状为 ,元素个数为 ,占用显存大小为 。
-
对于 矩阵乘法,需要保存中间激活 ,两个张量的形状都是 ,占用显存大小合计为 。
-
对于 函数,需要保存函数的输入 ,占用显存大小为 ,这里的 表示注意力头数。
-
计算完 函数后,会进行dropout操作。需要保存一个mask矩阵,mask矩阵的形状与 相同,占用显存大小为 。
-
计算在 上的attention,即 ,需要保存 score ,大小为 ;以及 ,大小为 。二者占用显存大小合计为 。
-
计算输出映射以及一个dropout操作。输入映射需要保存其输入,大小为 ;dropout需要保存mask矩阵,大小为 。二者占用显存大小合计为 。
因此,将上述中间激活相加得到,self-attention的中间激活占用显存大小为 。接下来分析分析Decoder layer中MLP的中间激活:
-
第一个线性层需要保存其输入,占用显存大小为 。
-
激活函数需要保存其输入,占用显存大小为 。
-
第二个线性层需要保存其输入,占用显存大小为 。
-
最后有一个dropout操作,需要保存mask矩阵,占用显存大小为 。
对于MLP块,需要保存的中间激活值为 。
另外,self-attention块和MLP块分别对应了一个layer normalization。每个layer norm需要保存其输入,大小为 。2个layer norm需要保存的中间激活为 。
综上,每个层需要保存的中间激活占用显存大小为 。对于 层transformer模型,还有embedding层、最后的输出层。embedding层不需要中间激活。总的而言,当隐藏维度 比较大,层数 较深时,这部分的中间激活是很少的,可以忽略。因此,对于 层模型,中间激活占用的显存大小可以近似为 ,这个结果与文本长度关系密切。
下面以GPT3-175B为例,对比下文本长度对模型参数与中间激活的显存大小的影响。假设数据类型为 FP16 。
| 模型名 | 参数量 | 层数 | 隐藏维度 | 注意力头数 |
|---|---|---|---|---|
| GPT3 | 175B | 96 | 12288 | 96 |
GPT3的模型参数量为175B,占用的显存大小为 。GPT3 模型需要占用350GB的显存。
假设 GPT3 输入的 。对比不同的文本长度下占用的中间激活:
当 时,中间激活占用显存为
,大约是模型参数显存的0.79倍;
当 时,中间激活占用显存为
,大约是模型参数显存的2.68倍。
可以看到长度仅仅到 4K,显存占用就出现了剧烈增加,同时 GPU onchip 的 memory 就显得更加捉襟见肘(因此也就出现了 FlashAttention 这类算法)。因此如何解决长文本带来的巨量显存开销成为关键及核心问题。
1.2 长文本问题的解决思路
当前,为了实现更长长文本的支持,解决思路主要可以分为两个阶段:
-
阶段一:在预训练阶段尽可能支持更长的文本长度
为实现这一阶段目标,通常采用并行化 (parallelism) 方法将显存占用分摊到多个 device,或者改造 attention 结构,避免显存占用与文本长度成二次关系。 -
阶段二:在 SFT 或推理阶段尽可能外推到更大长度
为实现这一阶段目标,通常也是需要在两个方面进行考虑:-
对位置编码进行外推
-
优化 At
-
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【Java+SpringBoot】房屋交易系统(源码+项目定制开发+代码讲解+答辩教学+计算机毕设选题)
- 从零实现一套低代码(保姆级教程)【后端服务】 --- 【17】实现页面的增删改查接口
- 操作系统-第六章-磁盘调度算法(使用C++和vector实现)
- 快速实现图片重命名(统一命名或按数字顺序命名)
- 基于SSM酒店后台管理系统【源码】【最详细运行文档】
- Java电影购票小程序在线选座订票电影
- 文本生成精准图像字幕,谷歌等开源PixelLLM
- 【OpenBMC】的内部README 模板
- flask flask-sqlalchemy sqlit3
- 手机的恢复功能急需改进