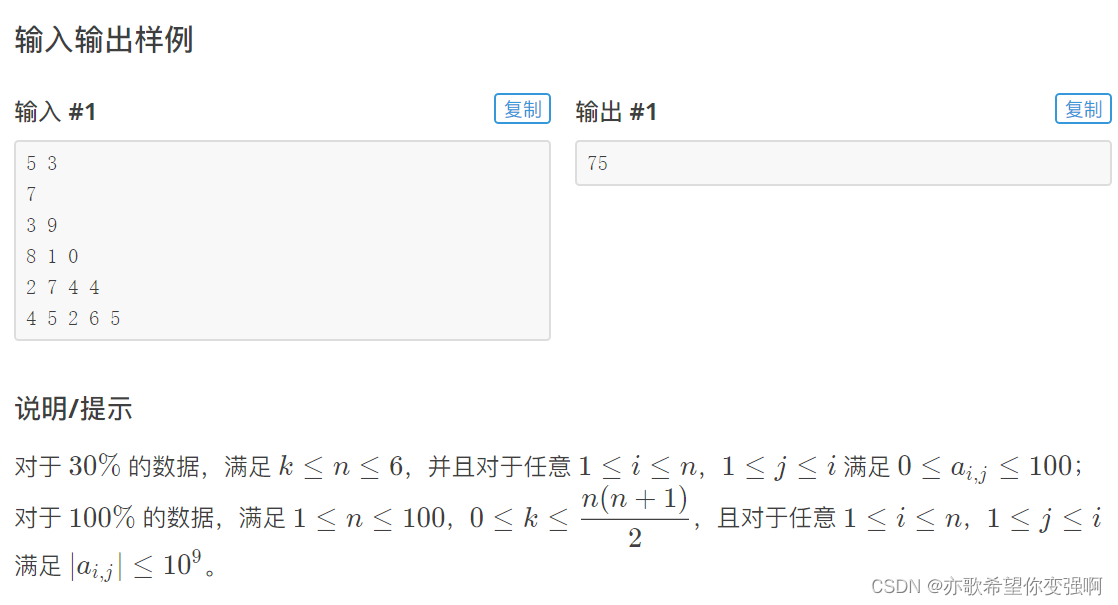
【算法每日一练]-动态规划（保姆级教程 篇14） #三倍经验 #散步 #异或和 #抽奖概率

目录

?今日知识点：

金字塔的正反dp两种方案，转移方程取决于dp的具体含义

取模实现循环走m步回到原点的方案

在统计上升子序列的时候使用最小结尾元素进行标记，一举两得

将亏本的概率转换各种情况的方案，然后统计亏本的情况的方案数烦求概率

三倍经验

散步

?异或和

抽奖概率?

---

三倍经验

思路：

首先不要考虑那么复杂，如果只是取数，但不考虑加倍的操作，那么就简单很多，只需要从下层想上层推导即可。保证每此都是最优解就行了。

这个时候f[i][j]从f[i-1][j]和f[i-1][j-1]中来。那么自然：

f[i][j]=max(f[i-1][j],f[i-1][j-1]) +a[i][j]。

然后我们再考虑要成3倍的情况，因为每个点可以对应是否有3倍的情况，而且这个消耗情况也要记录下来。所以需要开三维来表示。

设置f[i][j][k]表示在耗费次3倍操作下 且走到i，j对应的最优解。
?转移方程：

?f[i][j][l]=max(f[i-1][j][l],f[i-1][j-1][l])+a[i][j]; （当前数没有消耗次数）

?f[i][j][l]=max(f[i][j][l],max(f[i-1][j][l-1],f[i-1][j-1][l-1])+a[i][j]*3（当前数消耗次数了）
? 最终需要在f[n][i][0~k]中找答案

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=105,INF=-3e9;
int n,k;
ll a[N][N],f[N][N][N],ans=INF;
int main(){
	cin>>n>>k;
	for(int i=1;i<=n;i++)
	for(int j=0;j<=n;j++)
	for(int l=0;l<=k;l++)
	f[i][j][l]=INF;
	for(int i=1;i<=n;i++)
	for(int j=1;j<=i;j++){
		cin>>a[i][j];
		for(int l=0;l<=min(k,i);l++){
			if(l==0)
			f[i][j][l]=max(f[i-1][j][l],f[i-1][j-1][l])+a[i][j];
			else{
			f[i][j][l]=max(f[i-1][j][l],f[i-1][j-1][l])+a[i][j];
			f[i][j][l]=max(f[i][j][l],max(f[i-1][j][l-1],f[i-1][j-1][l-1])+a[i][j]*3);
				
			}
		}
	}
	for(int i=1;i<=n;i++)
	for(int l=0;l<=min(k,n);l++)
	ans=max(ans,f[n][i][l]);
	cout<<ans;
}

上面的是正向写法(也就是从上到下)。

当然也可以从下到上写：

?设置f[i][j][k]表示从i，j从开始消耗k次对应的最优解。

那么f[i-1][j-1]和f[i-1][j]就应该借此更新：（然后再拆成是否乘3倍，那就是4个式子）

????????????f[i-1][j-1][k]=max(f[i-1][j-1][k],f[i][j][k]+a[i-1][j-1]);
?? ??? ??? ?f[i-1][j-1][k+1]=max(f[i-1][j-1][k+1],f[i][j][k]+a[i-1][j-1]*3);
?? ??? ??? ?f[i-1][j][k]=max(f[i-1][j][k],f[i][j][k]+a[i-1][j]);
?? ??? ??? ?f[i-1][j][k+1]=max(f[i-1][j][k+1],f[i][j][k]+a[i-1][j]*3);?? ?

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll ans=-0x3f3f3f3f,f[110][110][110],a[110][110];
int n,m;
int main(){
	memset(f,-0x3f3f3f3f,sizeof(f));
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	for(int j=1;j<=i;j++)
		cin>>a[i][j];
	for(int i=1;i<=n;i++){
		f[n][i][0]=a[n][i];
		f[n][i][1]=a[n][i]*3;
	}
	for(int i=n;i>=2;i--)
	for(int j=1;j<=i;j++)
		for(int k=0;k<=min(n-i+2,m);k++){
			f[i-1][j-1][k]=max(f[i-1][j-1][k],f[i][j][k]+a[i-1][j-1]);
			f[i-1][j-1][k+1]=max(f[i-1][j-1][k+1],f[i][j][k]+a[i-1][j-1]*3);
			f[i-1][j][k]=max(f[i-1][j][k],f[i][j][k]+a[i-1][j]);
			f[i-1][j][k+1]=max(f[i-1][j][k+1],f[i][j][k]+a[i-1][j]*3);	
		}
	for(int i=0;i<=min(n,m);i++){
		ans=max(f[1][1][i],ans);
	}
	cout<<ans;
}

?可以会有人有疑问：既然(i,j)可以到(i+1,j)和(i+1,j+1)，为什么不是f[i][j]=max(f[i+1][j],f[i+1][j+1])这个式子呢？

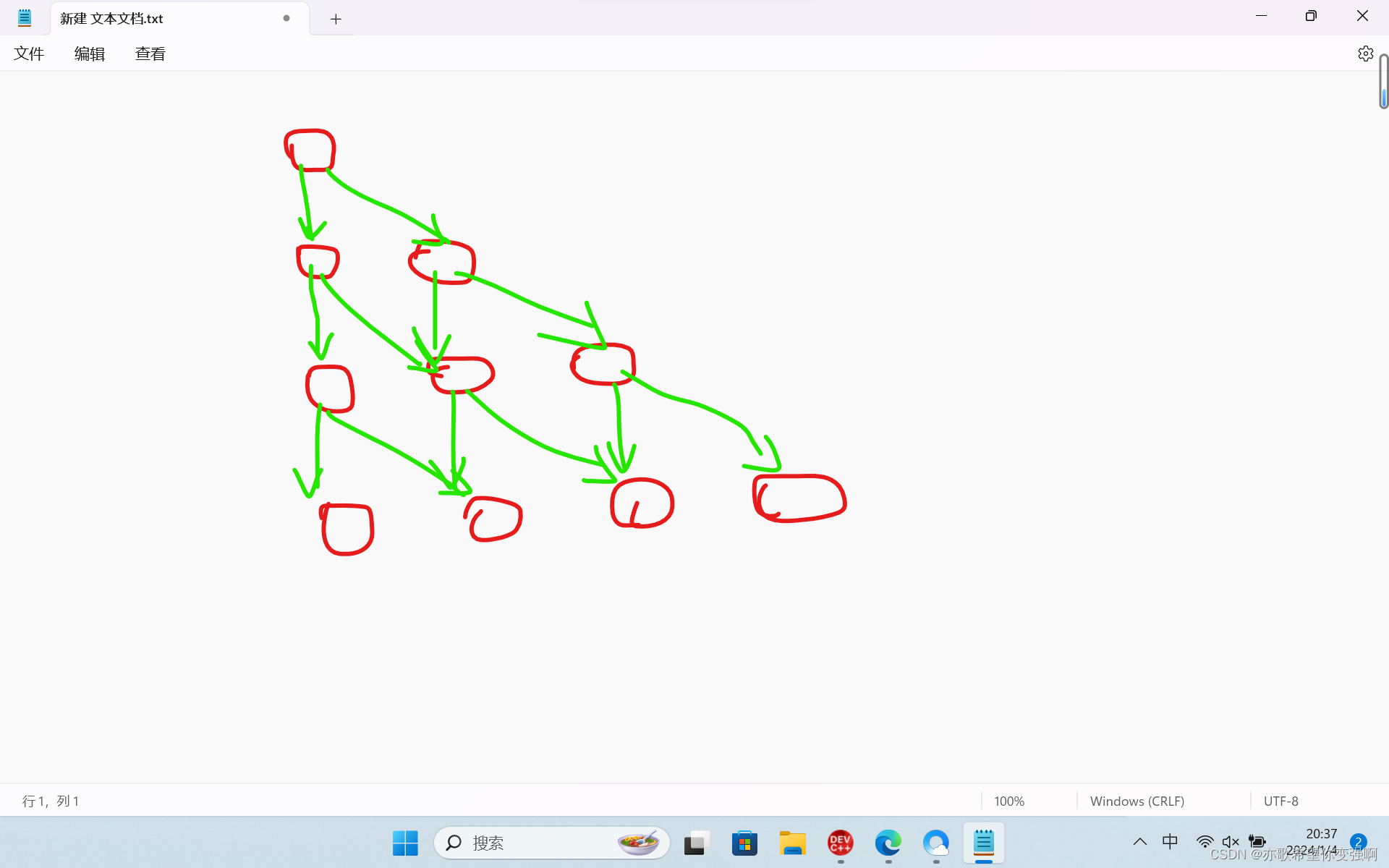
上图是正确的更新路线，举个例子：f[3][2]只能被f[2][1]和f[2][2]更新，因为只有这两个点才能到f[3][2]，所有才有了f[i][j]=max(f[i-1][j],f[i-1][j-1])这个式子。?

OK解释完了！

????????

????????

散步

思路：

?设置dp[i][j]表示已经走了i步，然后到达j。然后循环可以用取模实现，但是取模一定是0~n-1，所以需要进行映射。

转移方程：dp[i][j]=dp[i-1][(j+1)%n]+dp[i-1][(j-1+n)%n]

最终dp[m][0]就是答案。

#include <bits/stdc++.h>
using namespace std;
int dp[35][35],n,m;
int main(){
	cin>>n>>m;
	dp[0][0]=1;
	for(int i=1;i<=m;i++)
	for(int j=0;j<n;j++)
		dp[i][j]=dp[i-1][(j+1)%n]+dp[i-1][(j-1+n)%n];
	cout<<dp[m][0];
}

????????

?????????

?异或和

给一个长n的序列a1，a2……an，寻找在a的所有递增子序列(可以为空)的异或和中出现的数。

输入：? ? ? ? ? ? ? ? ? ? 输出：

2? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?4

1 5? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 0 1 4 5

思路：

题意就是统计异或和，不过是仅统计所有上升子序列的异或和，那么就在每次更新上升子序列的时候就打一次标记，用什么打标记，当然直接使用数组元素最方便。
所以：设置dp[i]表示异或和为i的满足题意的最小结尾元素。（里面存的是最小的结尾元素）
dp[j]<a[i]时候(i可以拼在j后面)：更新dp[j^a[i]]=min(dp[j^a[i],a[i])（标记了那个新异或和出现了）
最后统计有哪些dp被使用过，就说明这些数是答案
?

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,a[N],dp[N];

int main(){
	memset(dp,0x3f3f3f3f,sizeof(dp));
	dp[0]=0;
	cin>>n;
	for(int i=1;i<=n;i++)cin>>a[i];
	for(int i=1;i<=n;i++)
	for(int j=0;j<=550;j++)
		if(dp[j]<a[i]) 
		dp[j^a[i]]=min(dp[j^a[i]],a[i]);
	vector<int> ans;
	for(int i=0;i<=550;i++)
		if(dp[i]!=0x3f3f3f3f) ans.push_back(i);
	cout<<ans.size()<<'\n';
	for(int i:ans)
		cout<<i<<" ";
	
}

????????

????????

抽奖概率?

有一个抽奖活动：抽一个2元，可能会抽出1，2，3，4元（概率相等）。

问抽n次，亏本的概率是多少(奖金小于本金)？纯赚超过一半本金的概率是多少

输入：2? ? ? ? ? ?输出：3/16（分数时候输出最简分数）

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?3/16

思路：

直接求概率不太容易。而且还要最简分数，那么就转化乘求方案数就会具体很多。

设置dp[i][j]表示已经抽奖i次且拿到了总额为j的方案数.dp[i][j]=dp[i-1][j-1,2,3,4]即可。

最后的最简分数可以使用gcd函数完成。
?

#include <bits/stdc++.h>
using namespace std;
int dp[40][160],n;
int gcd(int a,int b){return b==0?a:gcd(b,a%b);}

int main(){
	cin>>n;
	dp[1][1]=dp[1][2]=dp[1][3]=dp[1][4]=1;
	for(int i=1;i<=n;i++)
	for(int j=i;j<=4*n;j++){
		for(int k=1;k<=4;k++)
			if(j>k) dp[i][j]+=dp[i-1][j-k];
	}
	int sum1=0,sum2=0,sum=1;
	for(int i=n;i<2*n;i++)
		sum1+=dp[n][i];
	for(int i=3*n+1;i<=4*n;i++)
		sum2+=dp[n][i];
	for(int i=1;i<=n;i++)
		sum*=4;
	int k=gcd(sum1,sum);
	cout<<sum1/k<<"/"<<sum/k<<'\n';
	k=gcd(sum2,sum);
	cout<<sum2/k<<"/"<<sum/k<<'\n';

}