MATLAB信号处理与应用 读书笔记 一
发布时间:2023年12月25日
完成了基本操作,今天组数也正常,需要对应解决fsctrl文件中的信号处理相关
- 重点关注4傅里叶变换,6FIR滤波器,10信号处理中的应用
- 字符的链接['aa','bb'];
N1=8;N2=16;
n=0:N-1;k1=0:N1-1;k2=0:N2-1;
w=2*pi*(0:2047)/2048;
Xw=(1-exp(-j*4*w))./(1-exp(-j*w));
xn=[(n>=0)&(n<=4)];
X1k=fft(xn,N1);
X2k=fft(xn,N2);
subplot(3,2,1);
plot(w/pi,abs(Xw));
xlabel('w/pi');ylabel('X1');
subplot(3,2,2);
plot(w/pi,angle(Xw));- FFT用DFT原理,理解起来还是吃力
Fs=1000;
T=1/Fs; %采样周期
L=2000;
t=(0:L-1)*T; %绘图的时间点
x=0.7*sin(2*pi*50*t)+sin(2*pi*700*t); %真实信号
y=x+2*randn(size(t)); %噪声叠加
subplot(121);
% plot(Fs*t(1:50),y(1:50));
plot(Fs*t,x);
title('时域图');
xlabel('t(s)');
ylabel('y(t)');
NFFT=2^(nextpow2(L));
Y=fft(y,NFFT)/L;
f=Fs/2*linspace(0,1,NFFT/2+1);
subplot(122);
plot(f,2*abs(Y(1:NFFT/2+1)));
title('频谱');
xlabel('f');
ylabel('|Y(f)|');FFT绘图部分,原信号:

叠加上随机噪声

plot画图,画连续的也需要进行点数离散化,点数够多,看起来就是连续的;

NFFT=2^(nextpow2(L)); %得到离采样点数最近的指数第一个要点,需要得到采样点对应的指数,这个指数在FFT中需要,若不是最近的指数,则求出的
实际使用L代替NFFT,得到的频点值完全是对应信号值,所以NFFT值意义在哪?
Y=fft(y,NFFT)/L; y的值和点数进行FFT计算,结果除以y进行归一化;
f=Fs/2*linspace(0,1,NFFT/2+1); 用Linspace得到0~1内NFFT个点值,再乘以FS/2得到奈奎斯特采样区间轴
plot(f,2*abs(Y(1:NFFT/2+1))); 对应的Y取绝对值,实际为幅值,因为求得的Y为实数,由于频谱折叠,所以要乘以2。如若不加abs,则信号谱的虚部将被忽略,造成幅值很小。
如果用全谱来看,则fs/2是保留奈奎斯特区间,abs是得实部虚部幅值,2*是将折叠得幅值相加。
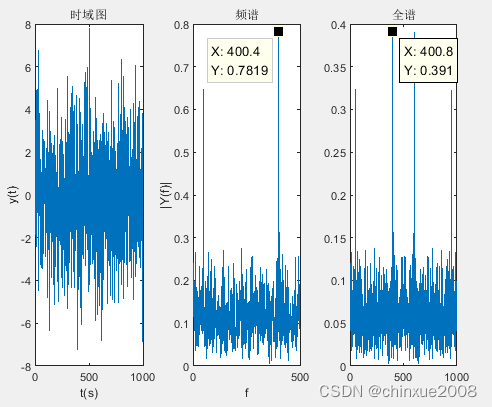
文章来源:https://blog.csdn.net/weixin_37281967/article/details/135208053
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Java标识符规则解析
- 已知IP地址,求能容纳一定数量IP地址的DHCP服务器的主机数量和子网掩码
- 算法题Python常用内置函数、方法、技巧汇总(其四:数字)
- 【程序员英语】【美语从头学】初级篇(入门)(笔记)Lesson1-Lession5(打招呼、礼貌、姓名年龄和国籍、介绍、职业)
- 深度迁移学习
- 带你手把手解读frejail沙盒源码(0.9.72版本) (六)fldd
- 华夏教师期刊投稿方式投稿邮箱
- 计算机软考小白问题解答
- 三国游戏(寒假每日一题+贪心、枚举)
- 数据结构OJ实验6-二叉树的遍历以及应用