Python - 深夜数据结构与算法之 Stack & Queue

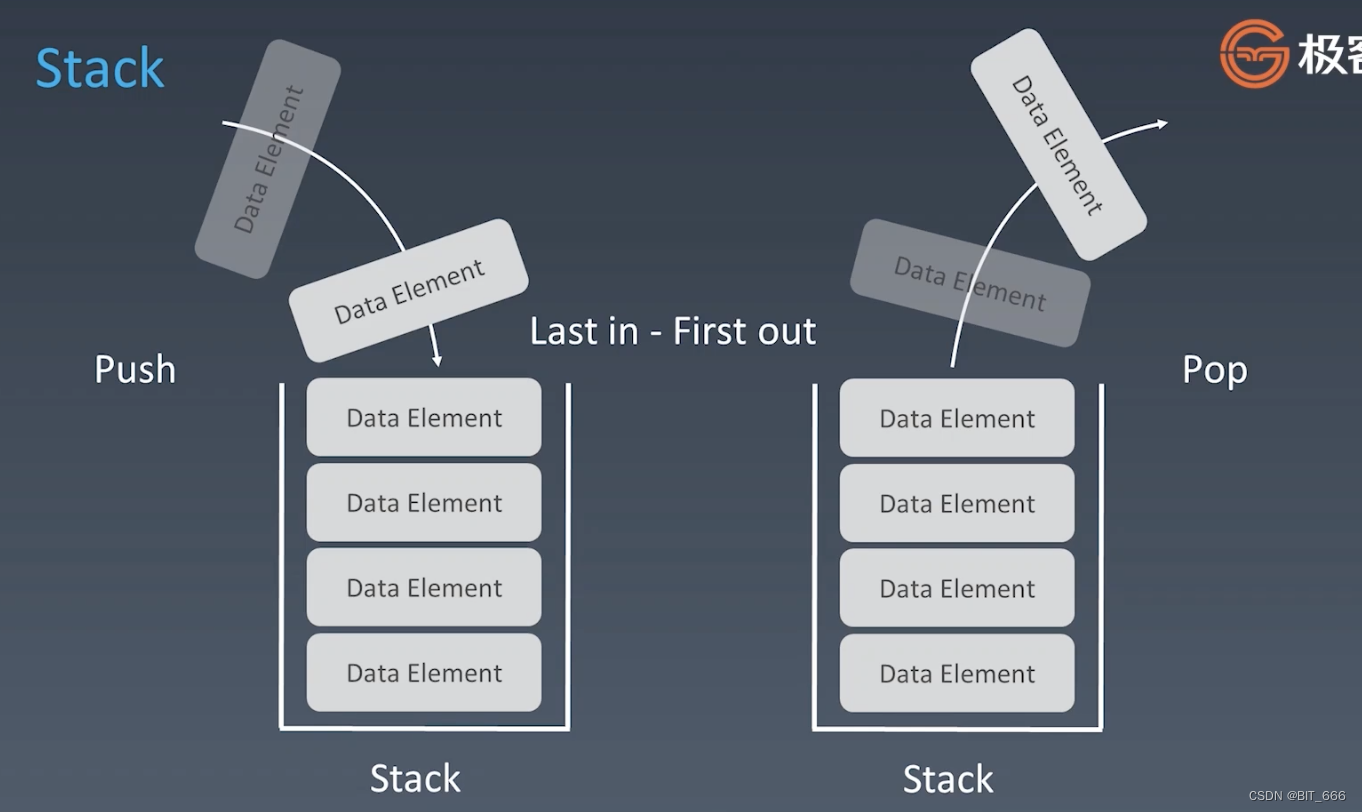
Stack 是一种先进后出的数据结构，即 Last in First out，通常情况下通过 push 或者 offer 将数据压入栈，通过 pop 弹出栈顶元素并返回。其添加和删除节点的时间复杂度均为 O(1)，但是查找一个元素的时间复杂度是 O(n)，因为我们需要遍历整个栈结构才能找到这个元素。生活中栈的应用有很多，我们每天都用的垃圾桶就和栈在结构上就很像，我们先扔进去的垃圾在最底下，最晚扔进去的垃圾在最上面。

2.Queue 队列

队列是一种先进先出的数据结构，即 Last in Last out、First in First out，通常可以通过 push?向队列尾部添加元素，通过 pop?获取队首元素，和 Stack 一样，其添加和删除节点的时间复杂度均为 O(1)，但是查找一个元素的时间复杂度为 O(n)。为了优化查找元素的时间，还有一类数据结构名为优先队列即 Priority Queue，其通过优化底层数据结构将查询的时间优化为 O(logN):

对于队列而言，其最常见的应用场景就是排队了，先到先得，而优先队列也很好理解，队伍里有 VIP 用户，对于 VIP 用户，需要按照其优先级优先出队。

3.DeQueue 双端队列

基于队列 Queue 的概念，后续还提出了 Double-End Queue 即双端队列，顾名思义，它的两端都支持 Push 和 Pop 操作，即两端都可以进出。其和队列 Queue 一样，插入和删除元素时间复杂度都是 O(1)，查找元素是 O(n)。

4.Stack、Queue 实现

Stack 和 Queue 都可以用 List[] 实现，Stack 栈使用 push 向栈内添加元素，使用 pop 返回栈顶元素；Queue 通过 enqueue 实现入队操作，通过 pop(index) 实现出队操作。下面给出数组类数据结构的时间复杂度:

?数据来源:?https://www.bigocheatsheet.com/

三.经典算法实战

上面介绍了 Stack、Queue 和 DeQueue 几种数据结构，下面挑选一些 LeetCode 上比较经典的算法，加深对这些数据结构的印象和使用技巧。这里约定一下每个算法的表现形式，Trapping-Water?代表算法名称，[x] 中括号里的 x 代表其对应 LeetCode 的第几题。

1.Valid-Parentheses [20]

有效括号:?https://leetcode.cn/problems/valid-parentheses

◆?题目分析

题目要求匹配括号字符串，其可以使 "[](){}" 这样，也可以是 "((()))" 这样。我们需要做的就是匹配每个左右括号，其满足新进后出的规律，对于 "[](){}" 比较简单，'['?先进，遇到 ']'?再出，依次匹配即可；对于 "({[]})" 我们先将 "({[" 依次压入栈，随后等待 "]})" 依次匹配它们并 pop 带走，可以看到最左侧的 '(' 是最先进栈的，而它是最后等到 ')' 来匹配，所以最后一个出，非常典型的先进后出。

◆????????触底反弹

#!/usr/bin/python
# -*- coding: UTF-8 -*-

class Solution(object):
    def isValid(self, s):
        """
        :type s: str
        :rtype: bool
        """

        # 奇数个 char 肯定不对
        if len(s) % 2 != 0:
            return False

        # 括号对应关系
        m = {"(": ")", "{": "}", "[": "]"}

        # 记录括号的栈
        stack = []

        for char in s:
            # 左括号压入栈
            if char in m.keys():
                stack.append(m[char])
            elif char in m.values():
                # 右括号到栈里找括号，找不到或找错说明不匹配
                if stack == [] or char != stack.pop():
                    return False
            else:
                # 特殊情况，防止异常的字符
                return False
        # 括号数量不匹配 or 数量为偶数
        return stack == []

由于题目只规定了字符串有 3 种类型，所以我们预先构造了左右括号的映射用于判断二者是否匹配。最开始判断字符串为奇数直接退出，因为奇数个括号肯定匹配不完。剩下遇到左括号就进栈右括号，遇到右括号就 pop 匹配，只要二者不相等就退出 False。

2.Trapping-Water [42]

接雨水:?https://leetcode.cn/problems/trapping-rain-water

◆????????题目分析

通过非负整数数组代表柱子高度，柱子凹槽的部门可以接雨水，求接水的量其实就是求凹槽的总面积。这一题和下面的求柱子最大矩形面积比较类似，根据木桶效应，能接到雨水需要中间的柱子低，两边的柱子比中间柱子高即可。

所以针对我们每一根内部即中间的柱子，我们只需要找其左侧和右侧的最高柱就能计算其接水面积，min(left_max - right_max) 代表当前桶的高度，cur_heigth 代表桶底多高，二者相减即为雨水量，如果前面小于等于后面那么相减会得到非正整数，那就就接不到雨水了，反之高度差多少就能接多少，遍历完内部的柱子 1: len-1，雨水总面积也就求出来了。这道题目是面试的经典题目，其内部的思想其实也很很多题目相同，下面实践一下。?

◆????????暴力开工

class Solution(object):
    def trap(self, height):
        res = 0
        
        for i in range(len(height)):
            # 左右两根柱子无法计算
            if i == 0 or i == len(height) - 1: continue
            
            # 记录左右的 max
            lHight = max(height[:i])
            rHight = max(height[i + 1:])
           
            # 计算面积 
            res1 = min(lHight, rHight) - height[i]
            if res1 > 0:
                res += res1
        return res

忽略左右两侧的单独柱子，对内部的柱子依次计算桶边 min(lHight、rHight) 和桶底 height[i] 的差距，大于0代表当前索引 i 可以接雨水的面积。根据 "你立马想到必不能过" 原理，如果我们想法清晰且简单快速实现，那么本题必出幺蛾子，继续想其他办法。

◆????????循环利用

class Solution(object):
    def trap(self, height):
        # 1.初始化左右 max 柱子
        cur_height = len(height)
        left_bound = [height[0]] + [0] * (cur_height - 1)
        right_bound = [0] * (cur_height - 1) + [height[-1]]

        # 2.更新左右 max 柱子
        for i in range(1, cur_height):
            # 左柱子，所以是 i-1 和新来的 i 比大小
            left_bound[i] = max(left_bound[i - 1], height[i])
            # 右柱子，新来的 i 和之前的 i+1 比大小
        for i in range(cur_height - 2, -1, -1):
            right_bound[i] = max(right_bound[i + 1], height[i])

        # 3.木桶效应
        re = 0
        for i in range(1, cur_height - 1):
            re += min(left_bound[i], right_bound[i]) - height[i]

        return re

暴力法中我们对于每一个中间的柱子 mid 都分别向左向右找最大，这个过程其实是重复的，我们可以一次性把左边和右边柱子的最高高度记录下来，随后根据计算方法 min(l_h, r_h) - h 直接遍历计算即可，上面通过两个辅助 List left_bound 和 right_bound 分别记录，最后根据木桶效应计算，相比暴力法节省了很多重复寻找的时间。

◆????????单调栈

    def trap(self, height):
        stack = [0]
        result = 0
        for i in range(1, len(height)):
            while stack and height[i] > height[stack[-1]]:
                # 打印日志 print(stack)
                mid_height = stack.pop()
                if stack:
                    # 雨水高度是 min(凹槽左侧高度, 凹槽右侧高度) - 凹槽底部高度
                    h = min(height[stack[-1]], height[i]) - height[mid_height]
                    # 雨水宽度是 凹槽右侧的下标 - 凹槽左侧的下标 - 1
                    w = i - stack[-1] - 1
                    # 累计总雨水体积
                    result += h * w
            stack.append(i)
        return result

单调栈的思路其实还是木桶原理，如果桶能够接到雨水，其一定是两边高中间低的情况，所以单调栈内栈底到栈顶是递减的，这里栈底相当于桶的左边，其余递减的元素相当于桶底，当遇到 height[i] > height[stack[-1]] 的情况时，说明对于栈顶所在元素索引 stack[-1] 而言，它桶的右边也找到了，所以就可以计算面积了。这里与前面暴力法竖的计算面积不同，单调栈采用横向面积计算，下面画图看一下，以下面 heigths = [5, 2, 1, 0, 4, 1, 1, 6] 为例，我们通过 stack 的情况分析计算过程:

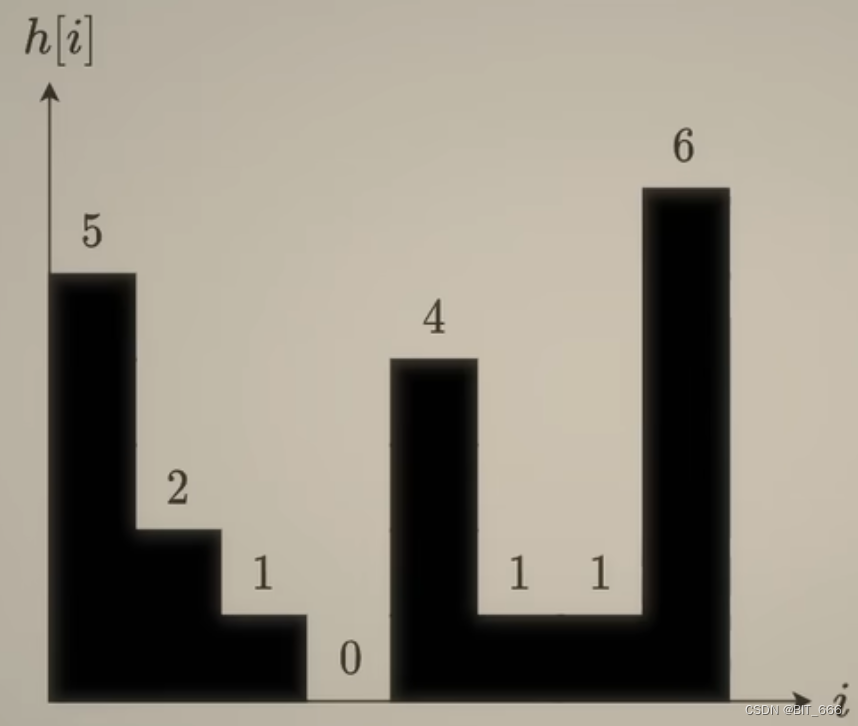
- [0, 1, 2, 3]

因为 5、2、1、0 是递减的，所以只执行 for 循环操作，while 判断的?height[i] > height[stack[-1]] 不执行，所以一次添加了 1、2、3 的索引。当遇到 heigth = 4 的时候，其满足 while 条件，此时对于 0 而言，可以计算其雨水面积:?

mid_height = stack.pop() = 0 # 中间柱子
h = min(height[stack[-1]], height[i]) - height[mid_height] # 水桶的低处
w = i - stack[-1] - 1 # 雨水量

中间柱子高度为 0，h = min(1, 4) - mid_height = 1，面积为 1 x 1 = 1

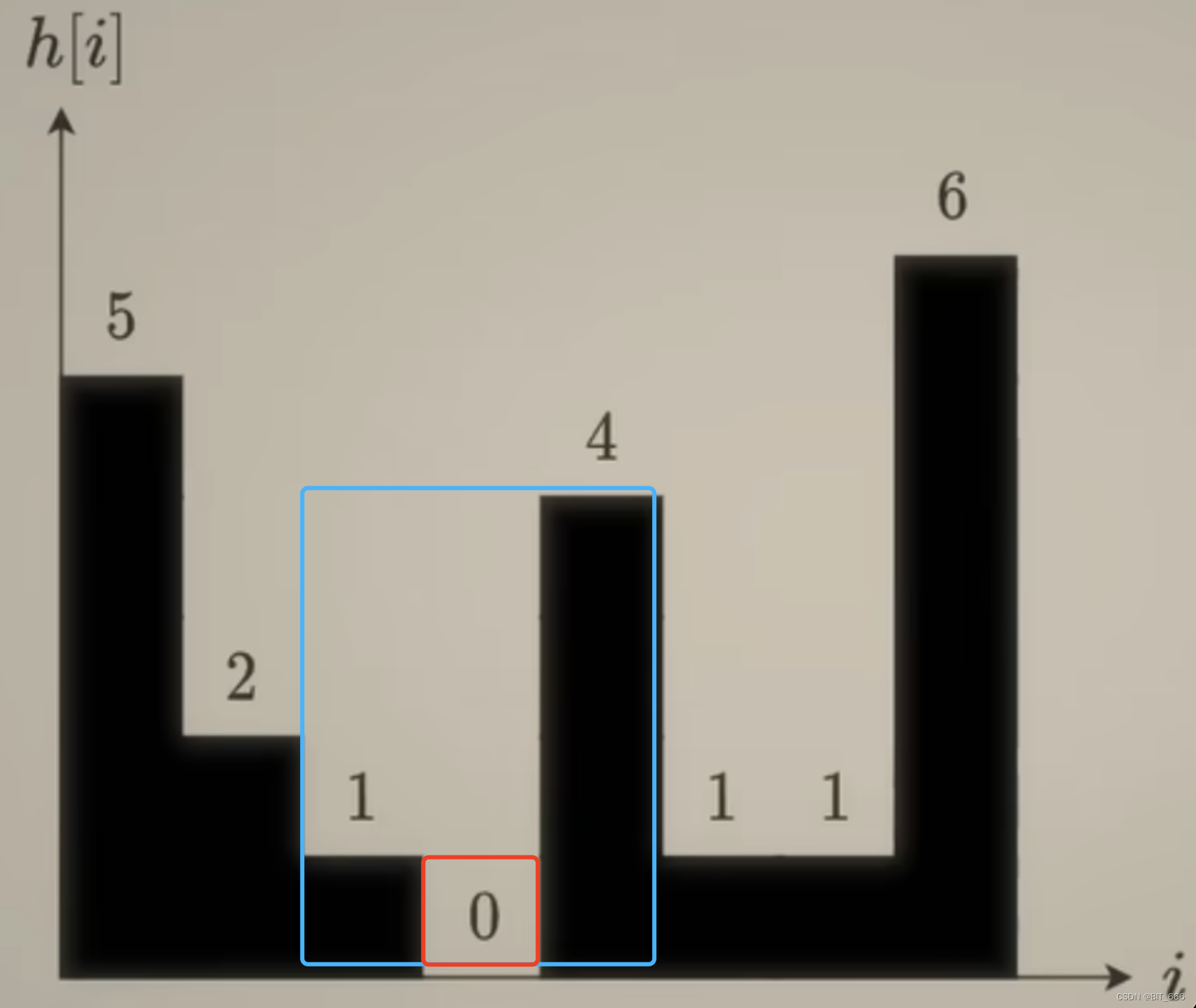
这里蓝框对应我们处理的三个元素，红框代表实际雨水面积。

-[0, 1, 2] -[0, 1]

这两个同上，因为 index=2?的 height=1 与 index=1?的 height=2 均小于 4，所以都会触发 while 逻辑计算面积，其面积如下所示，对于 index=2 而言，其对应面积为 2，index=1 而言面积为 6，这里计算完 mid = [index=1] 的棒子后，index=1 从 stack 中 pop，此时 stack 仅剩 [0]。

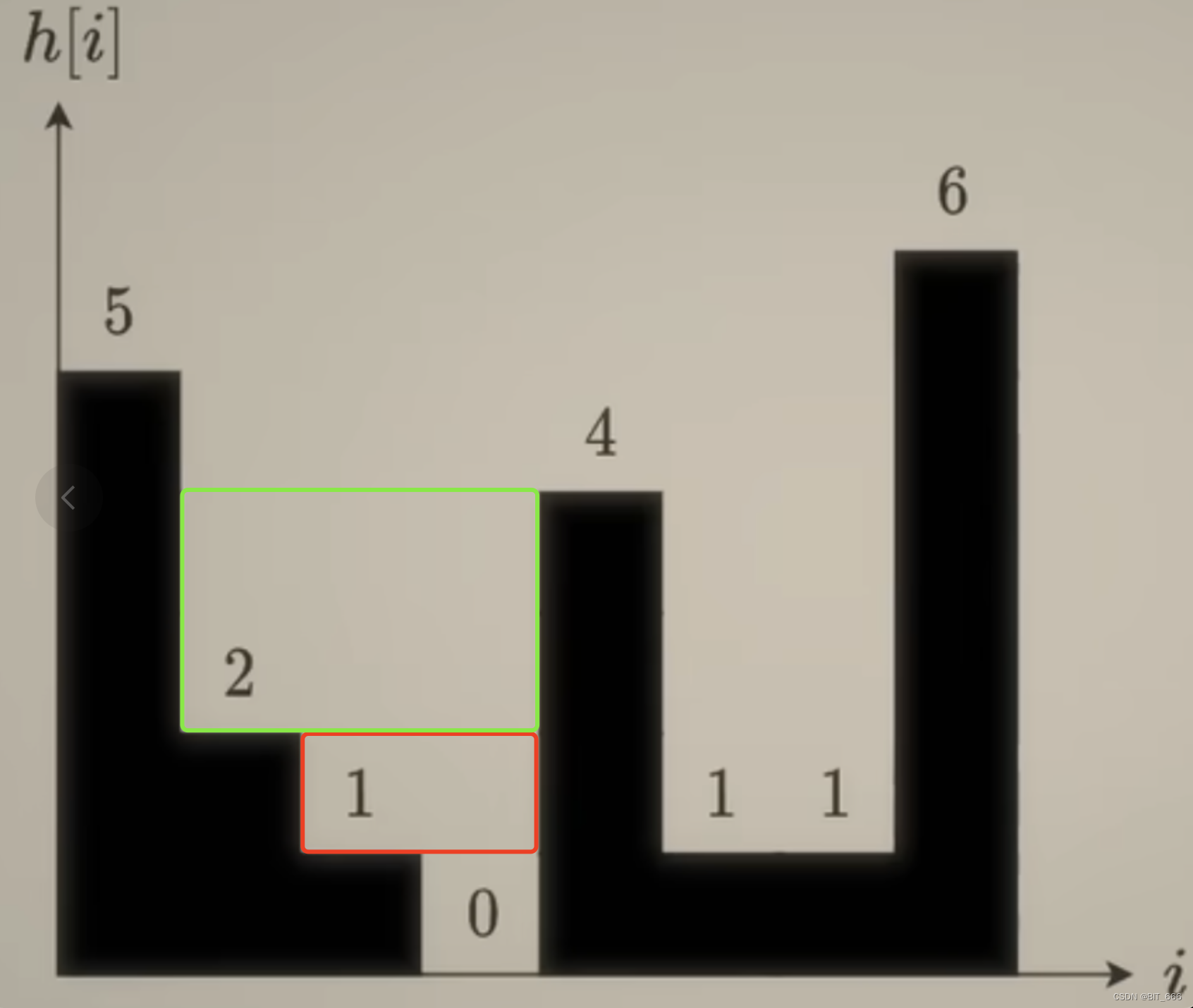
- [0, 4, 5, 6]

stack 剩下元素为 index = 0，height=5，由于后面的 4、1、1 对应的高度均小于5，所以他们的索引 4、5、6 均添加到栈中。此时元素 6 出现，其大于上一个 mid=1，所以开始计算雨水面积。其左柱子高度为1，右柱子高度为6，min(1,6) - mid_height = 0，所以索引 6 处对应的雨水面积为0，因为桶左边漏水。

- [0, 4, 5]

换到 index = 5 处的 1 时，其左柱子高度不再为 1，而是 4，所以 min(4, 6) - 1 = 3，此时宽度为 2，面积计算得6。

- [0, 4]

stack 将两个 1 弹出后，还剩 [0, 4]，此时 mid_height = 4，左柱子高度 5，右柱子高度 6，min(5, 6) - 4 = 1，但是宽度是 7 - 0 - 1 = 6，所以这里面积为 6。

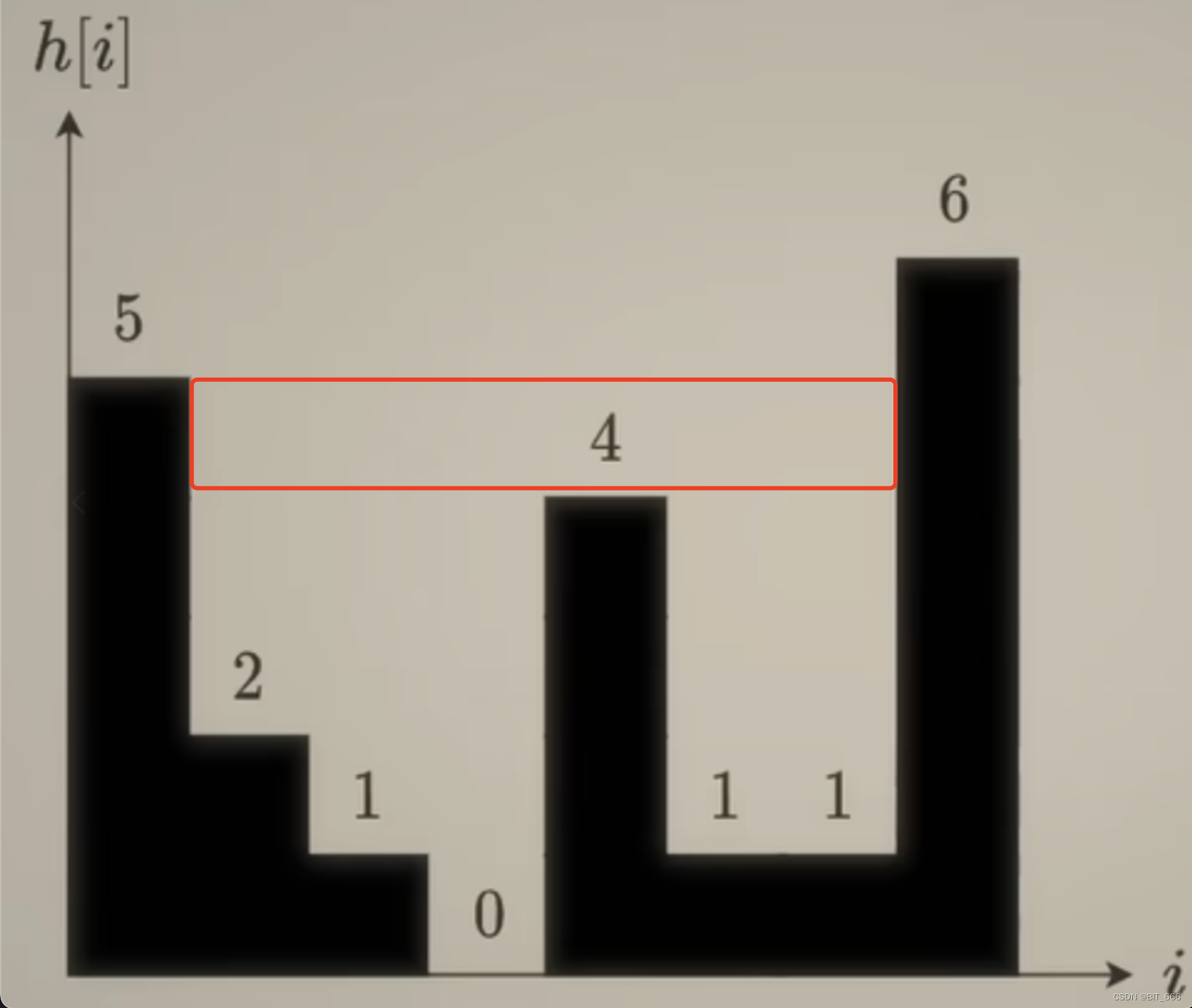
- [0]

mid = 4 的柱子索引弹出，height = 6 的索引进入 stack，这里满足 6>5 所以进入 while 逻辑，但是当 mid = index[0] 的中间柱子弹出后，不满足 if stack 条件了，所以遍历也就结束了，这是因为两个柱子不足以构成带底的水桶。综合上面的计算流程，我们其实是把水桶转了 90 度计算面积：

通过数形结合的方法，这道题的代码理解起来就不难了，难点在于单调栈的想法与实践，即什么时候需要使用单调栈。?单调栈就是保持栈内元素有序，当我们需要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置，就可以想到可以用单调栈了。而接雨水这道题目，我们需要寻找左右的最大元素，所以可以使用其来计算接雨水面积。

3.largest-Rectangle-Area [84]

最大矩形面积:?https://leetcode.cn/problems/largest-rectangle-in-histogram

◆????????题目分析

本题考察非负数组构成的列表表示的柱状图能够勾勒出的最大矩形面积，看到题目思考后，第一个思路比较快的出现，即遍历每一个柱子，向左向右寻找比其大的元素，使其能到达的最大宽度，这个方法很好理解，但是其时间复杂度为 o(n^2)，依照我们以往的惯例，这样大概率会在耗时上被卡掉。另外一种实现是利用单调栈，这个方法比较巧妙，一会看图理解一下。

◆????????左右开弓

class Solution(object):
    def largestRectangleArea(self, heights):
        """
        :type heights: List[int]
        :rtype: int
        """
        # 棒子数量
        bar = len(heights)

        # 记录当前最大值
        global_max = -1

        for i in range(bar):
            # 记录当前 h 与 w
            cur_height = heights[i]
            cur_width = 1

            # 向左 👈
            for left_index in range(i - 1, -1, -1):
                if heights[left_index] >= cur_height:
                    cur_width += 1
                else:
                    break

            # 向右 👉
            for right_index in range(i + 1, bar, 1):
                if heights[right_index] >= cur_height:
                    cur_width += 1
                else:
                    break

            cur_area = cur_height * cur_width
            global_max = max(global_max, cur_area)

        return global_max

遍历每一根柱子，初始宽度为自己 width = 1，向右 while 找比自己大的元素并将 width += 1，同理向左也一样，两个 while 停止后，根据自己的数值即 height x width 即可得到面积。图比较抽象，其代表每个 bar 能够生成的最大面积：

倒在了倒数第三个测试样例上，由于 o(n^2) 的时间复杂度，这个方法不是最优:?

◆????????单调栈

    def largestRectangleArea(self, heights):
        """
        :type heights: List[int]
        :rtype: int
        """
        size = len(heights)
        res = 0
        heights = [0] + heights + [0]

        # 放入哨兵结点，在循环中不用做非空判断
        stack = [0]
        size += 2

        for i in range(1, size):
            # 如果比当前对应位置索引小，说明 stack[-1] 处的有边界找到了
            while heights[i] < heights[stack[-1]]:
                cur_heigth = heights[stack.pop()]
                cur_width = i - stack[-1] - 1
                # 更新最大值
                res = max(res, cur_heigth * cur_width)
            stack.append(i)

        return res

上面的代码先不看，先捋一下思路，对于一根柱子而言，其左右没有比它再大的柱子时，它所对应的矩形也就确定下来了，只要其左右还有比他还高的柱子，它的 width 就能一直扩展。举个例子:

index = 0、heigth=6:

元素索引入栈，为什么是 index，因为宽度计算需要 index 相减，高度可以通过 index 获得，一举两得

index = 1、heigth=7 :

入栈，因为这里 7 > 6，所以对于 index = 0 处的 height=6，其右边界还没有确定，继续进行

index = 2、height=5:

计算 index = 1、heigth = 7 的面积，因为对于 7 而言，其左右都比他小，所以面积可以计算了，width = 2 - 0 - 1，height = 7，面积 Area = 7，此时对于 index = 1 位置的 height = 7 的柱子而言，它对应的矩形面积已经计算完毕了，所以栈里不需要它，此时 pop 即可。

这个时候还没完，index = 1 pop 弹出后，继续比较 5 < 6，所以对于 6 而言，其右边界也找到了，同理，计算面积 width = 2 - (-1) - 1，height = 6，Area = 12，此时 0 出栈。这里我们也理解了为什么 7 可以出栈了，一方面是 7 对应的矩阵计算完了，另一方面 7 是两边最高的，它走了也不会影响两边的元素计算面积。

0 计算弹出后，索引 2 对应的 5 压入栈，左边没有元素了，所以继续向右寻找边界

index = 3、height=2:

?索引 3 高度为 2 小于上一个高度 5，所以索引 2 高度 5?的右边界找到了，此时 width = 3 - (-1) - 1，height = 5，Area = 15，index = 2 出栈，index = 3 入栈

index ++:

后面继续，4、5、9 均大于 2，所以都压入栈，等到 3 出现时，[3 < 9] 9 对应的面积 Area=9 然后弹出，[3 < 5]5 对应的面积 Area = 10 然后弹出，[3 < 4] 4 对应的面积 Area = 12 弹出。到了 [3 > 2] 此时第一层 For 循环结束，还有 3 和 2 的面积没有算，我们先计算 3 Area = 12，再计算 2? Area = 16，最终最大面积为 16。这里把动图直接放过来，大家可以下载下来一帧一帧看:

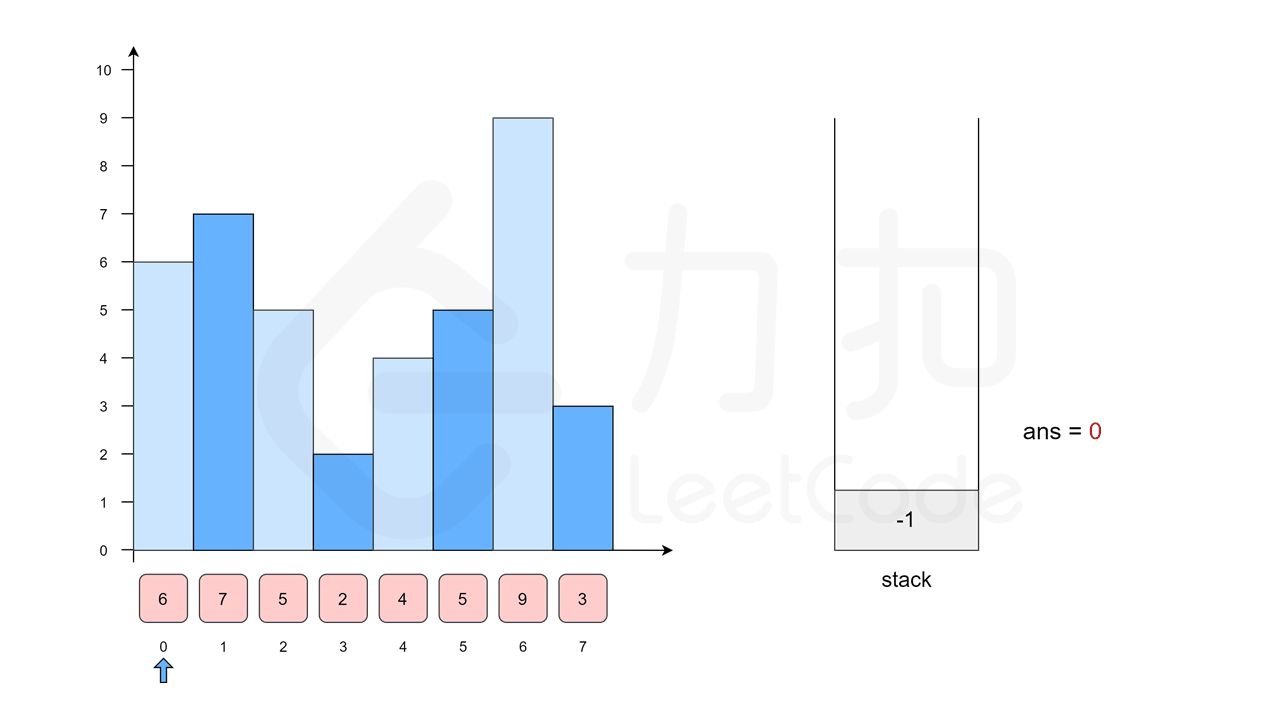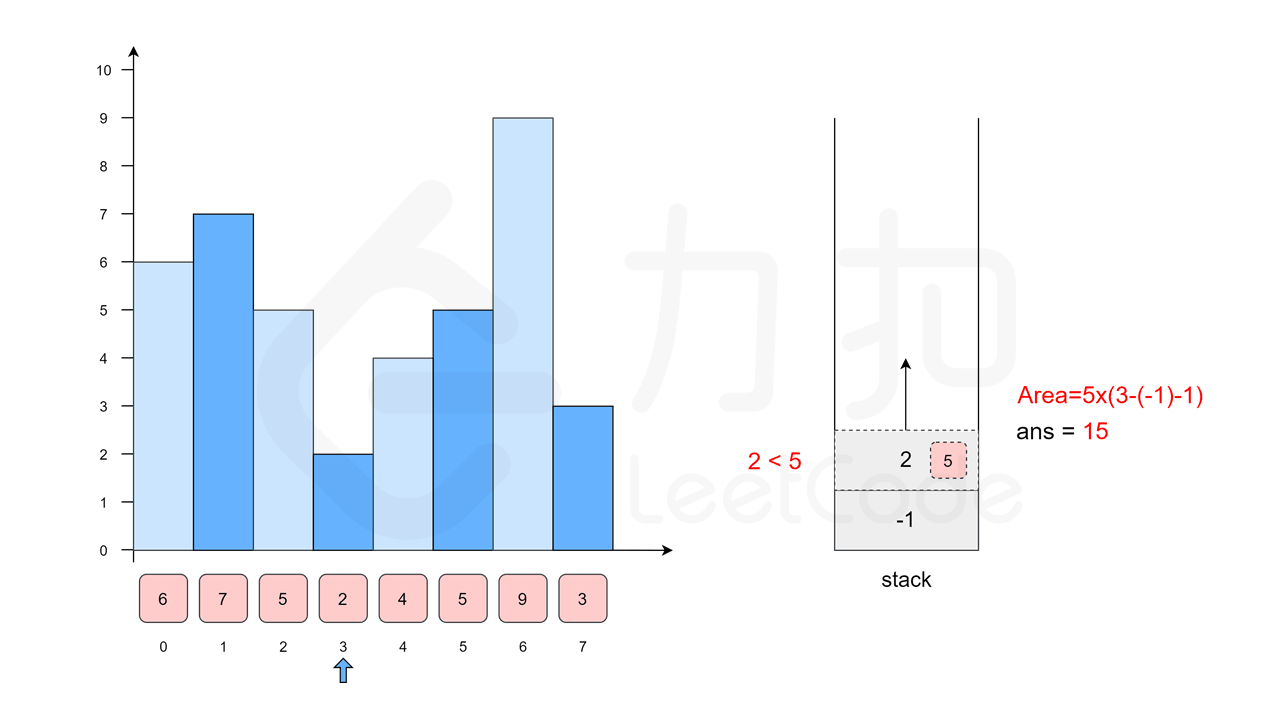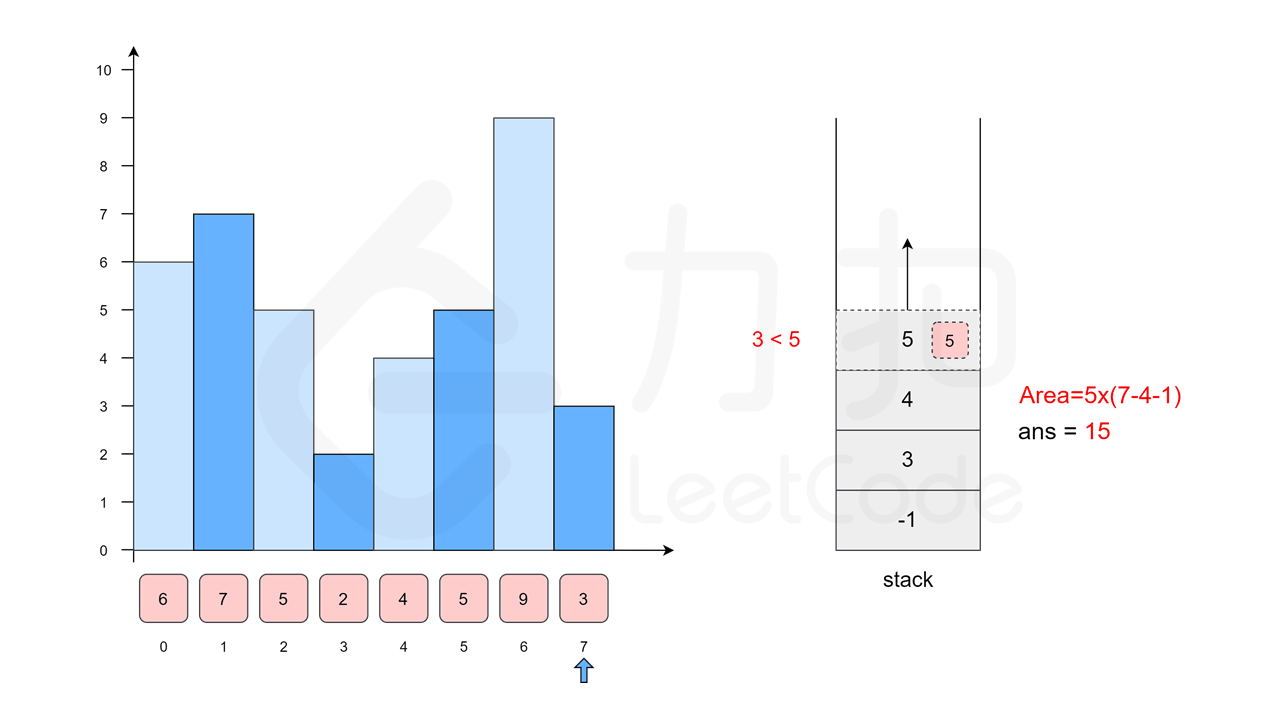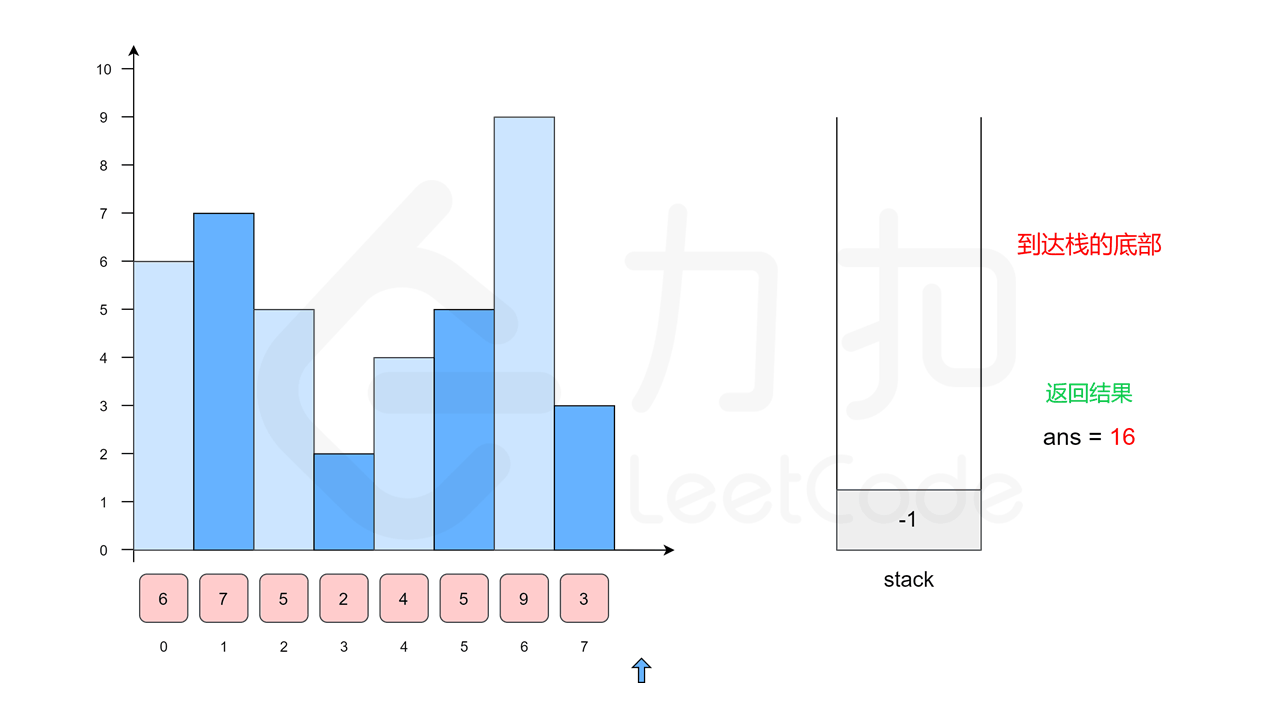
-> 哨兵节点?

上面说了这么多，红框内计算面积和入栈出栈的操作我们可以看懂了，但是代码里的 heigths 前后各加了一个 0，这里还需要研究研究。首先基于上面的步骤，我们看原始代码有哪几个问题:

from typing import List


class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        size = len(heights)
        res = 0

        stack = []

        for i in range(size):
            while len(stack) > 0 and heights[i] < heights[stack[-1]]:
                cur_height = heights[stack.pop()]

                while len(stack) > 0 and cur_height == heights[stack[-1]]:
                    stack.pop()

                if len(stack) > 0:
                    cur_width = i - stack[-1] - 1
                else:
                    cur_width = i

                res = max(res, cur_height * cur_width)
            stack.append(i)

        while len(stack) > 0 is not None:
            cur_height = heights[stack.pop()]
            while len(stack) > 0 and cur_height == heights[stack[-1]]:
                stack.pop()

            if len(stack) > 0:
                cur_width = size - stack[-1] - 1
            else:
                cur_width = size
            res = max(res, cur_height * cur_width)

        return res

可能出现栈为空的情况，此时需要 while stack 一直判断 empty:

这里初始化 stack = [0]

最后遍历完毕后，例如刚才出现的 2、3?的情况，还需要再加一次处理:

这里再 heights 两边各增加一个 0，左边这个高度为 0 的柱子由于它小于任何一个非负整数，它肯定不会出栈，因此不会被 pop 出去；右边这个高度为 0 的柱子一定比数组中任何一个元素都小，所以它会触发所有元素出栈并计算面积，这样避免了第二次的 while 补充处理。

总的来说这个题目非常巧妙，让我自己想估计是想不出来，要么多看理解要么背诵的节奏了。

4.Min-Stack [155]

最小栈:?https://leetcode.cn/problems/min-stack

◆????????题目分析

本题考察一方面是自定义实现栈的功能，另一方面是在栈的基础上增加一个 getMin 的方法，要在常数时间内检索到最小元素，如果每次都遍历一遍栈的话效率很低，所以我们可以引入一个辅助栈空间，当我们主栈元素 push 时，辅助栈 push 当前元素加入后整个栈堆的最小值，这样元素和对应的最小值就同时存储了。

◆????????辅助空间


class MinStack(object):

    def __init__(self):
        self.stack = []
        # math.inf
        self.min_stack = [2147483647]


    def push(self, val):
        """
        :type val: int
        :rtype: None
        """
        self.stack.append(val) # 元素入栈
        self.min_stack.append(min(val, self.min_stack[-1])) # 最小元素入栈
        # 任何时刻，栈内元素的最小值就在辅助栈的栈顶


    def pop(self):
        """
        :rtype: None
        """
        self.stack.pop()
        # 对应的最小值也需要更新
        self.min_stack.pop()


    def top(self):
        """
        :rtype: int
        """
        return self.stack[-1]


    def getMin(self):
        """
        :rtype: int
        """
        return self.min_stack[-1]

这一题用数组实现栈的功能其实比较基础，主要拓展的是引入辅助空间的思想，需要明确一点就是 "任何时刻，栈内元素的最小值就在辅助栈的栈顶"，所以新加入元素时其只要和栈顶元素比较就能知道当前全局最小是谁。同时需要看清算法要求，例如 pop 只是删除栈顶的元素但是没有要求返回，top 要求获取栈顶的元素但是没有要求弹出。?

5.Max-Sliding-Window [239]

滑动窗口最大值:?https://leetcode.cn/problems/sliding-window-maximum

◆????????题目分析

一个整数列表中包含一个大小为 k 的滑动窗口，从左到右移动，并记录每次滑动窗口中的最大值。整个过程就像是卷积核卷积一样，随着卷积核移动得到新的卷积结果。本题上来的很直接的就想到直接遍历 0 到 len-k+1?即可，把 k 个窗口的 max 记录下来，下面试一下。

◆????????遍历求解

class Solution(object):
    def maxSlidingWindow(self, nums, k):
        """
        :type nums: List[int]
        :type k: int
        :rtype: List[int]
        """

        re = []

        for i in range(0, len(nums) - k + 1):
            re.append(max(nums[i: i + k]))

        return re

先看上面的算法本身，len(nums) - k 后还有 k 个元素剩余，此时还能构成最后一个 k-window，所以 range 遍历时需要 len(nums) - k + 1。其次再看运行结果，官方给出的示例包含一个巨大的数组和巨大的 k，这里数组遍历 o(n) 的时间复杂度无法避免，因为我们总归要把全部数组看完，所以超时问题就在 max 函数这里了，是寻求最大值的时间超了，所以后续的算法要想办法优化 max 的计算。?

◆????????双端队列

    def maxSlidingWindow(self, nums, k):

        # 存放结果
        res = []

        # 构造双端队列，从大到小排列，即最大值在最左边
        queue = collections.deque()

        # 遍历索引、数值
        for i, num in enumerate(nums):
            # 第一步: 判断当前最大值是否为k数组外的元素，是的话移除, 判断索引: i-k 即可
            if queue and queue[0] == i - k:
                queue.popleft()

            # 第二步: 剩下的都是 k 数组的元素，比 num 小的都扔掉，因为是取最大
            while queue and nums[queue[-1]] < num:
                queue.pop()

            # 第三步: 当前元素加入到 k 数组中
            queue.append(i)

            # 第四步: 从 k-1 处开始向 res 添加值，因为第一个 k 数组的末尾索引为 k - 1，最大值在 head
            if i >= k - 1:
                res.append(nums[queue[0]])

        return res

这里构造双端队列维护 k-window 中的最大值情况，最大值的索引始终放在 dequeue 的左端，遍历到新元素时，首先判断队首索引是否为 i-k，如果是需要移除，因为 i-k 已经不属于当前的 k-window；如果不是，说明最大的元素是 i-k+1 或者 i-k+2 对应的元素，比较然后弹出即可，这里第二步会把最大的元素对应的索引保留在队首；第三步添加当前索引，因为是移动窗口，所以当前元素不能丢失，其还需要和后面元素比较；最后就是添加 max 值了，因为 k-window 至少需要 k 个元素构成，所以当索引达到 k-1 时是第一个窗口 k-windwo - [0, k-1]，从现在开始向 res 添加结果，最大值为左侧索引对应的值。

6.MyCircularDeque [641]

双端队列实现:?https://leetcode.cn/problems/design-circular-deque

◆????????题目分析

这个题目和前面的 Min-Stack 最小栈在技巧上考察不多，主要考察的是数组的基本操作以及对栈和队列的概念是否清晰，这两个题的实现可以帮助大家更好的理解栈和队列的数据结构特点与使用。双端队列即两端均可插入和弹出的队列，这里我们依旧使用 List[] 实现。

◆????????List 依旧

#!/usr/bin/python
# -*- coding: UTF-8 -*-

# 设计循环双端队列

class MyCircularDeque(object):

    # 用 List 实现 Queue
    def __init__(self, k):
        """
        :type k: int
        """
        self.queue = []
        self.max_size = k

    # 使用 insert(index, value) 实现队首插入元素
    def insertFront(self, value):
        """
        :type value: int
        :rtype: bool
        """
        if len(self.queue) < self.max_size:
            self.queue.insert(0, value)
            return True
        else:
            return False

    # 使用 pop(value) 实现队尾插入元素
    def insertLast(self, value):
        """
        :type value: int
        :rtype: bool
        """
        if len(self.queue) < self.max_size:
            self.queue.append(value)
            return True
        else:
            return False

    # 使用 del(index) 实现删除指定位置元素
    def deleteFront(self):
        """
        :rtype: bool
        """
        if self.queue:
            del self.queue[0]
            return True
        else:
            return False

    # 使用 pop() 实现删除队尾元素
    def deleteLast(self):
        """
        :rtype: bool
        """
        if self.queue:
            self.queue.pop()
            return True
        else:
            return False

    def getFront(self):
        """
        :rtype: int
        """
        if self.queue:
            return self.queue[0]
        else:
            return -1

    def getRear(self):
        """
        :rtype: int
        """
        if self.queue:
            return self.queue[-1]
        else:
            return -1

    def isEmpty(self):
        """
        :rtype: bool
        """
        return len(self.queue) == 0

    def isFull(self):
        """
        :rtype: bool
        """
        return len(self.queue) == self.max_size

队首添加 insert、队尾添加?append、返回 pop、删除 del，过程中注意判断队列长度，避免空数组和越界的情况。?

四.总结

上面讲解了 Stack 栈与 Queue 队列的基本概念以及 LeetCode 里一些基本的算法操作，本文介绍了栈与队列的 List 实现方法，同时图文分析了两道经典的算法题目: 最大矩形面积与接雨水，其用到的单调栈方法十分巧妙，大家可以多多练习。除此之外，辅助空间、双指针等常用的方法我们也有再次用到，这些方法都是常用的技巧，也需要多多复习与练习。这里算法题目的解法不一定是最优的，大家有更多扩展需求也可以到乐扣官网查看更多题解和思路。

文章来源:https://blog.csdn.net/BIT_666/article/details/135004608
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！