【LeetCode每日一题合集】2023.12.11-2023.12.17 (?二维前缀和+二维差分 & 珂朵莉树)
文章目录
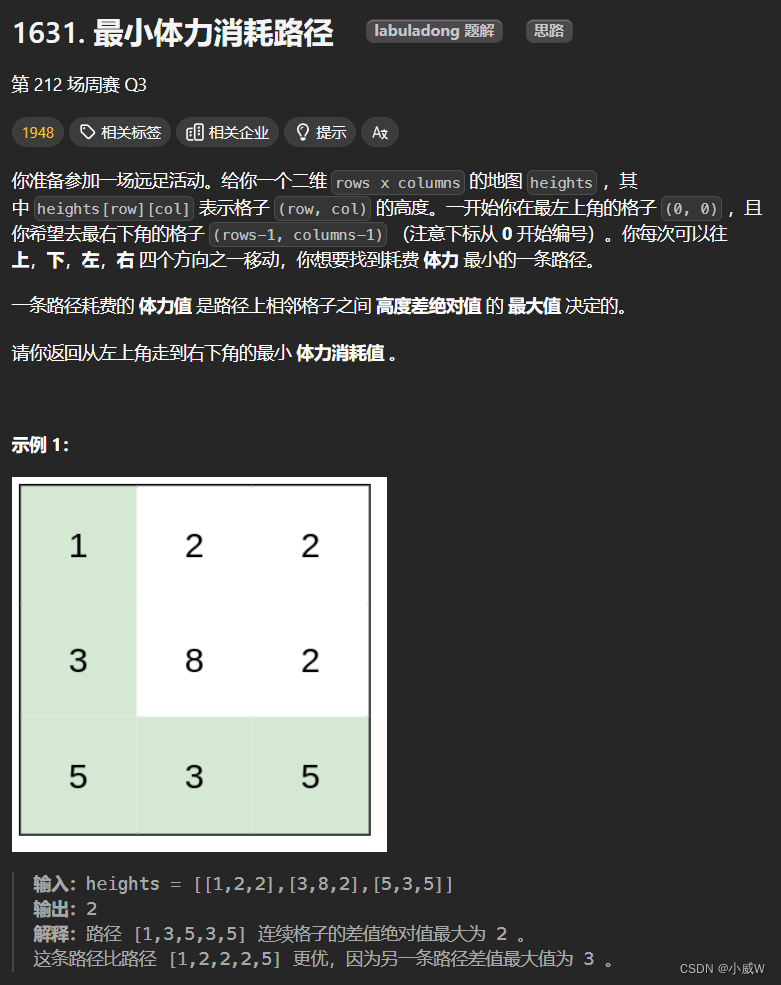
1631. 最小体力消耗路径?🐂
提示:
rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
1 <= heights[i][j] <= 10^6
解法1——二分查找
二分查找答案,每次用 BFS 检查是否合理。
时间复杂度是
m
n
l
o
g
C
mnlogC
mnlogC
class Solution {
int m, n;
int[][] heights;
int[] dx = {-1, 0, 1, 0}, dy = {0, -1, 0, 1};
public int minimumEffortPath(int[][] heights) {
m = heights.length;
n = heights[0].length;
this.heights = heights;
int l = 0, r = 999999;
while (l < r) {
int mid = l + r >> 1;
if (check(mid)) r = mid;
else l = mid + 1;
}
return l;
}
public boolean check (int mx) {
Queue<int[]> q = new LinkedList<>();
boolean[][] st = new boolean[m][n];
st[0][0] = true;
q.offer(new int[]{0, 0});
while (!q.isEmpty()) {
int[] cur = q.poll();
int x = cur[0], y = cur[1];
if (x == m - 1 && y == n - 1) return true;
for (int k = 0; k < 4; ++k) {
int nx = x + dx[k], ny = y + dy[k];
if (nx >= 0 && nx < m && ny >= 0 && ny < n && !st[nx][ny] && Math.abs(heights[x][y] - heights[nx][ny]) <= mx) {
q.offer(new int[]{nx, ny});
st[nx][ny] = true;
}
}
}
return false;
}
}
解法2——并查集
把数据当作一个图,将所有边放入列表并从小到大排序,之后逐个枚举边,将两边的点放入并查集中,直到起点和终点位于同一个集合,此时的边就是答案。
class Solution {
int[] p;
public int minimumEffortPath(int[][] heights) {
int m = heights.length, n = heights[0].length;
List<int[]> edges = new ArrayList<>();
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
int id = i * n + j;
if (i > 0) {
// 把这个点和上面的点这条边放进去
edges.add(new int[]{id - n, id, Math.abs(heights[i][j] - heights[i - 1][j])});
}
if (j > 0) {
// 把这个点和左面的点这条边放进去
edges.add(new int[]{id - 1, id, Math.abs(heights[i][j] - heights[i][j - 1])});
}
}
}
Collections.sort(edges, (x, y) -> {
return x[2] - y[2];
});
p = new int[m * n];
Arrays.setAll(p, e -> e);
int ans = 0;
// 从小到大枚举每个边
for (int[] edge: edges) {
int x = edge[0], y = edge[1], v = edge[2];
p[find(x)] = find(y);
if (find(0) == find(m * n - 1)) { // 加入这个边之后,0和m*n-1联通了
ans = v;
break;
}
}
return ans;
}
public int find(int x) {
if (x != p[x]) p[x] = find(p[x]);
return p[x];
}
}
解法3——最短路 Dijkstra
【算法基础:搜索与图论】3.4 求最短路算法(Dijkstra&bellman-ford&spfa&Floyd)
使用堆优化的 Dijkstra 算法。
class Solution {
int[] dx = {-1, 0, 1, 0}, dy = {0, -1, 0, 1};
public int minimumEffortPath(int[][] heights) {
int m = heights.length, n = heights[0].length;
PriorityQueue<int[]> pq = new PriorityQueue<>((x, y) -> {
return x[2] - y[2];
});
pq.offer(new int[]{0, 0, 0});
int[][] dist = new int[m][n];
for (int i = 0; i < m; ++i) Arrays.fill(dist[i], Integer.MAX_VALUE);
dist[0][0] = 0;
boolean[][] seen = new boolean[m][n];
while (!pq.isEmpty()) {
int[] edge = pq.poll();
int x = edge[0], y = edge[1], d = edge[2];
if (seen[x][y]) continue;
if (x == m - 1 && y == n - 1) break;
seen[x][y] = true;
for (int i = 0; i < 4; ++i) {
int nx = x + dx[i], ny = y + dy[i];
if (nx >= 0 && nx < m && ny >= 0 && ny < n && Math.max(d, Math.abs(heights[nx][ny] - heights[x][y])) < dist[nx][ny]) {
dist[nx][ny] = Math.max(d, Math.abs(heights[nx][ny] - heights[x][y]));
pq.offer(new int[]{nx, ny, dist[nx][ny]});;
}
}
}
return dist[m - 1][n - 1];
}
}
2454. 下一个更大元素 IV(双单调栈)
https://leetcode.cn/problems/next-greater-element-iv/?envType=daily-question&envId=2023-12-12

提示:
1 <= nums.length <= 10^5
0 <= nums[i] <= 10^9
解法1——双单调栈
一个单调栈处理第一个更大的数,另一个处理第二个更大的数字。
如何确保了 stk2 的单调性呢?因为先处理了 stk2,可以确保在 stk1 的数据推入 stk2 之前,stk2 中 <= nums[i] 的数据都被弹出了,即 stk2 中存留的数据一定 大于 从 stk1 推入 stk2 的数据。
class Solution {
public int[] secondGreaterElement(int[] nums) {
int n = nums.length;
int[] ans = new int[n];
Arrays.fill(ans, -1);
// 两个单调递减的单调栈
Deque<Integer> stk1 = new ArrayDeque<>(), stk2 = new ArrayDeque<>();
for (int i = 0; i < n; ++i) {
// 判断是否是第二个更大的数字
while (!stk2.isEmpty() && nums[i] > nums[stk2.peek()]) {
ans[stk2.pop()] = nums[i];
}
// 使用ls存下弹出的结果
List<Integer> ls = new ArrayList<>();
while (!stk1.isEmpty() && nums[i] > nums[stk1.peek()]) {
ls.add(stk1.pop());
}
for (int j = ls.size() - 1; j >= 0; j--) stk2.push(ls.get(j));
stk1.push(i);
}
return ans;
}
}
解法2——单调栈+优先队列
用一个单调队列代替其中一个单调栈,时间复杂度是 O ( n l o g n ) O(nlogn) O(nlogn)
class Solution {
public int[] secondGreaterElement(int[] nums) {
int n = nums.length;
int[] ans = new int[n];
Arrays.fill(ans, -1);
// 两个单调递减的单调栈
Deque<Integer> stk = new ArrayDeque<>();
PriorityQueue<Integer> pq = new PriorityQueue<>((x, y) -> nums[x] - nums[y]);
for (int i = 0; i < n; ++i) {
// 判断是否是第二个更大的数字
while (!pq.isEmpty() && nums[i] > nums[pq.peek()]) {
ans[pq.poll()] = nums[i];
}
while (!stk.isEmpty() && nums[i] > nums[stk.peek()]) {
pq.offer(stk.pop());
}
stk.push(i);
}
return ans;
}
}
2697. 字典序最小回文串(贪心)
提示:
1 <= s.length <= 1000
s 仅由小写英文字母组成
回文串的相对应位置,两两判断取较小者即可。
class Solution {
public String makeSmallestPalindrome(String s) {
int n = s.length();
char[] chs = s.toCharArray();
for (int l = 0, r = n - 1; l < r; ++l, --r) {
if (chs[l] < chs[r]) chs[r] = chs[l];
else chs[l] = chs[r];
}
return new String(chs);
}
}
2132. 用邮票贴满网格图?????(二维前缀和+二维差分)
https://leetcode.cn/problems/stamping-the-grid/description/?envType=daily-question&envId=2023-12-14

提示:
m == grid.length
n == grid[r].length
1 <= m, n <= 10^5
1 <= m * n <= 2 * 10^5
grid[r][c] 要么是 0 ,要么是 1 。
1 <= stampHeight, stampWidth <= 10^5
用前缀和快速检查一片区域是否有占据位置;
用差分快速检查一个位置是否被覆盖。
class Solution {
public boolean possibleToStamp(int[][] grid, int stampHeight, int stampWidth) {
int m = grid.length, n = grid[0].length;
int[][] sum = new int[m + 1][n + 1], diff = new int[m + 2][n + 2];
// 计算占据位置的前缀和
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
sum[i + 1][j + 1] = grid[i][j] + sum[i + 1][j] + sum[i][j + 1] - sum[i][j];
}
}
// 依次检查每个位置是否可以作为左上角,计算差分数组
for (int i = 0; i + stampHeight - 1 < m; ++i) {
for (int j = 0; j + stampWidth - 1 < n; ++j) {
int x = i + stampHeight, y = j + stampWidth;
int s = sum[x][y] - sum[i][y] - sum[x][j] + sum[i][j];
if (s == 0) {
diff[i + 1][j + 1]++;
diff[i + 1][y + 1]--;
diff[x + 1][j + 1]--;
diff[x + 1][y + 1]++;
}
}
}
// 还原差分数组
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
diff[i][j] += diff[i - 1][j] + diff[i][j - 1] - diff[i - 1][j - 1];
if (diff[i][j] == 0 && grid[i - 1][j - 1] == 0) {
return false;
}
}
}
return true;
}
}
关于 前缀和 和 差分 可见:【算法基础】1.5 前缀和与差分
力扣上有二维前缀和的模板题目:304. 二维区域和检索 - 矩阵不可变
2415. 反转二叉树的奇数层

提示:
树中的节点数目在范围 [1, 2^14] 内
0 <= Node.val <= 10^5
root 是一棵 完美 二叉树
解法1——BFS 交换值
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode reverseOddLevels(TreeNode root) {
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
boolean f = true;
while (!q.isEmpty()) {
int sz = q.size();
List<TreeNode> ls = new ArrayList<>();
for (int i = 0; i < sz; ++i) {
TreeNode cur = q.poll();
if (f && cur.left != null) {
ls.add(cur.left);
ls.add(cur.right);
}
if (cur.left != null) q.offer(cur.left);
if (cur.right != null) q.offer(cur.right);
}
if (f) {
for (int l = 0, r = ls.size() - 1; l < r; l++, r--) {
int t = ls.get(l).val;
ls.get(l).val = ls.get(r).val;
ls.get(r).val = t;
}
}
f = !f;
}
return root;
}
}
解法2——镜像DFS 🐂
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode reverseOddLevels(TreeNode root) {
dfs(root.left, root.right, 1);
return root;
}
public void dfs(TreeNode a, TreeNode b, int d) {
if (a == null) return;
if (d % 2 == 1) swap(a, b);
dfs(a.left, b.right, d + 1);
dfs(a.right, b.left, d + 1);
}
public void swap(TreeNode a, TreeNode b) {
int t = a.val;
a.val = b.val;
b.val = t;
}
}
2276. 统计区间中的整数数目(平衡二叉搜索树/珂朵莉树)?????
提示:
1 <= left <= right <= 10^9
最多调用 add 和 count 方法 总计 10^5 次
调用 count 方法至少一次
珂朵莉树是一种以近乎暴力的形式存储区间信息的一个数据结构。方式是通过set存放若干个用结构体表示的区间,每个区间的元素都是相同的。

class CountIntervals {
TreeMap<Integer, Integer> map = new TreeMap<>();
int cnt = 0;
public CountIntervals() {
}
public void add(int left, int right) {
Map.Entry<Integer, Integer> interval = map.floorEntry(right);
while (interval != null && interval.getValue() >= left) {
int l = interval.getKey(), r = interval.getValue();
left = Math.min(left, l);
right = Math.max(right, r);
cnt -= r - l + 1;
map.remove(l);
interval = map.floorEntry(right);
}
cnt += right - left + 1;
map.put(left, right);
}
public int count() {
return cnt;
}
}
/**
* Your CountIntervals object will be instantiated and called as such:
* CountIntervals obj = new CountIntervals();
* obj.add(left,right);
* int param_2 = obj.count();
*/
746. 使用最小花费爬楼梯(线性DP)
class Solution {
public int minCostClimbingStairs(int[] cost) {
int n = cost.length;
// dp[i]表示在第i层再走一步的最小花费
int[] dp = new int[n];
dp[0] = cost[0];
dp[1] = cost[1];
for (int i = 2; i < n; ++i) {
dp[i] = Math.min(dp[i - 1], dp[i - 2]) + cost[i];
}
return Math.min(dp[n - 1], dp[n - 2]);
}
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- vue 公众号开发,调用jssdk封装
- 【Docker】安装 Nginx 容器并部署前后端分离项目
- 【React】常见疑问的整理
- Java:Lambda表达式、方法引用
- 环境配置 | 史上最详细的Anaconda安装教程
- 持续领先 | 开源网安连续三年上榜ISC数字安全创新能力百强
- 讲个笑话 三角形是最有稳定性的结构
- 太阳光模拟器汽车耐老化太阳跟踪聚光户外加速老化试验
- 张驰课堂:激发学员兴趣,打造六西格玛绿带培训的互动学习环境
- Apache OFBiz RCE漏洞复现(CVE-2023-51467)