力扣70. 爬楼梯(动态规划 Java,C++解法)
Problem: 70. 爬楼梯
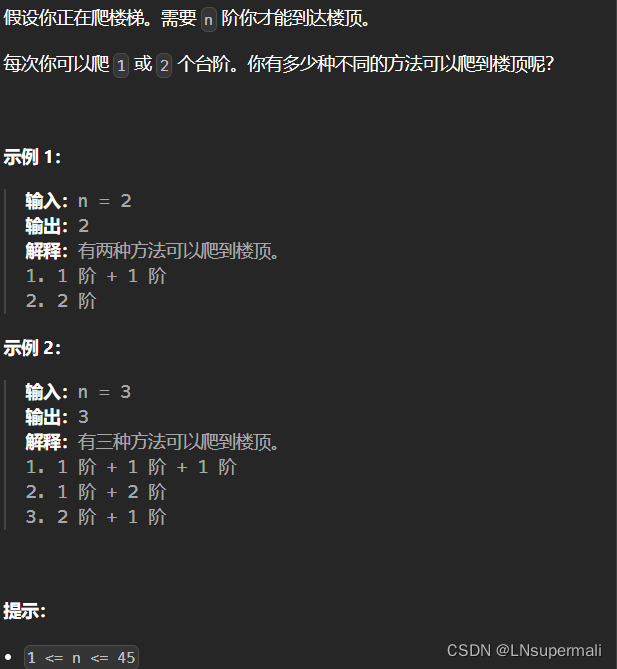
题目描述
思路
由于本题目中第i层台阶只能由于第i- 1层台阶和第i-2层台阶走来,所以可以联想到动态规划,具体如下:
1.定义多阶段决策模型:对于每一上台阶看作一种状态;
2.定义状态转移方程:int[] dp = new int[n + 1]用于记录第i个台阶可以走到的走法;dp[i] = dp[i - 1] + dp[i - 2];
解题方法
1.定义数组int[] dp = new int[n + 1]用于记录第i个台阶可以走到的走法
2.初始化dp[1] = 1; dp[2] = 2;
3.从dp数组下标为3处开始完成动态转移方程;
4.返回dp[n]
复杂度
时间复杂度:
O ( n ) O(n) O(n);其中 n n n为台阶数
空间复杂度:
O ( n ) O(n) O(n)
Code
class Solution {
/**
* Dynamic programing
* @param n The number of stage
* @return int
*/
public int climbStairs(int n) {
if (n <= 2) {
return n;
}
//Record how many moves there are on step i
int[] dp = new int[n + 1];
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; ++i) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
}
class Solution {
public:
int climbStairs(int n) {
if (n <= 2) {
return n;
}
vector<int> dp(n + 1);
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; ++i) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
};
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 阿里云服务器4核8G配置最新优惠价格表(2024活动报价)
- Linux read命令详解
- 无人售货机管理系统开发难点
- Redis事务操作
- 选择云服务器租用托管有哪些优势?
- [Python] pyqt6 - QTimer定时器介绍和使用场景(案例)
- 宠物空气净化器怎么挑选?猫用空气净化器品牌性比价推荐
- 奇偶校验,CRC循环冗余校验,海明码校验
- 基于SSM+Jsp的在线商城系统(有文档演示视频,java毕业设计)
- 钡铼LoRa网关实现大气污染、噪声和空气质量等环境参数监测