排序之希尔排序

希尔排序，也被称为缩小增量排序，是一种基于插入排序的算法。它通过比较相距一定间隔的元素，来工作，然后再逐渐减小间隔，直到整个数组排序完成。这种算法的主要优点是对于部分有序的数组，其效率非常高，可以达到线性排序的效率。

步骤：

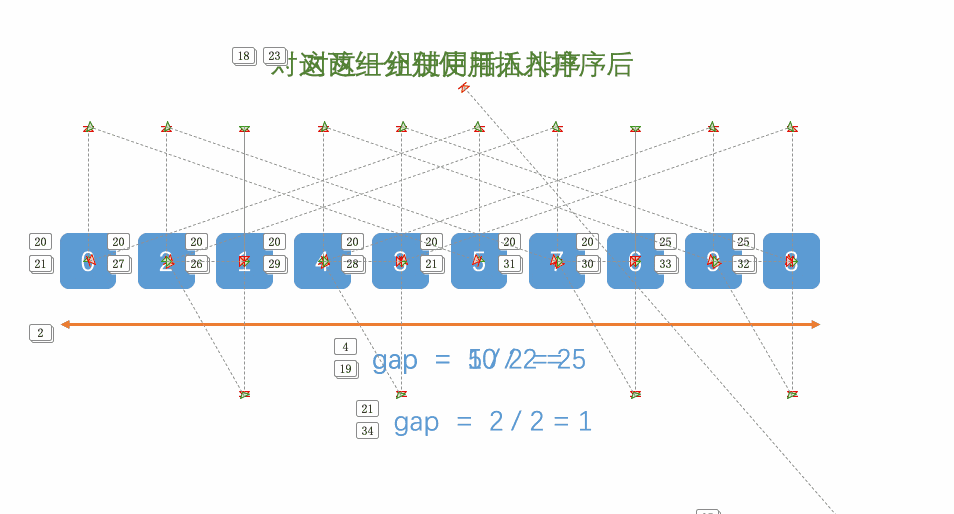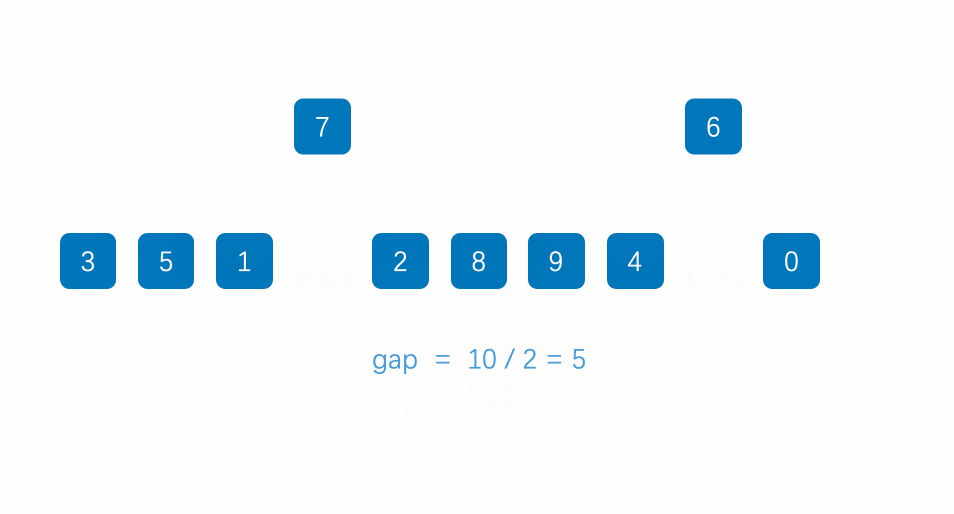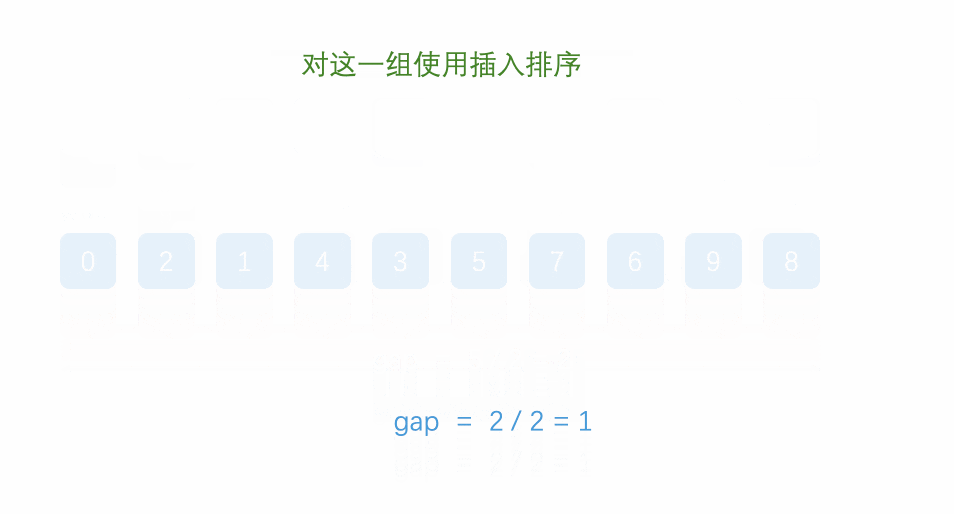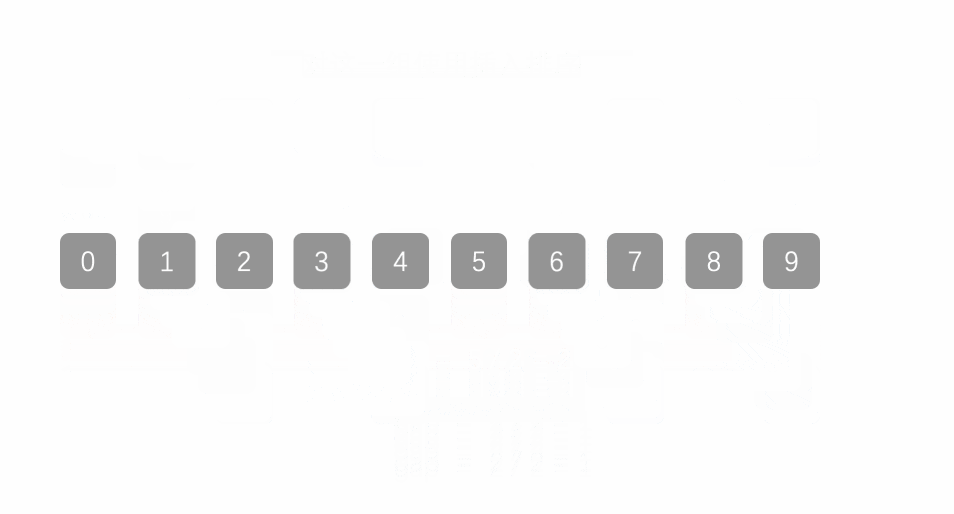
1. 按照数组长度的一半为间隔进行分组，在组内进行插入排序，小的数值到前边，大的数值在后边
2. 按照数组长度一半的一半为间隔继续分组，在组内继续进行插入排序
3. 按照数组长度一半的一半的一半为间隔继续分组，在组内继续进行插入排序
4. 直到步长为1的时候，整个数组成为一组

思路：
希尔排序，先将待排序列进行预排序，使待排序列接近有序，然后再对该序列进行一次插入排序，此时插入排序的时间复杂度为O(N)，?

时间复杂度平均：O(N^1.3)
空间复杂度：O(1)?

代码实现

下面是希尔排序的Java实现：

import java.util.Arrays;
//希尔排序
public class ShellSort {

	public static void main(String[] args) {
		int[] arr = {5,7,4,2,0,3,1,6};
		sort(arr);
		System.out.println(Arrays.toString(arr));
	}

	public static void sort(int[] arr) {
		for(int gap = arr.length/2;gap>0;gap/=2) {
			for(int i = gap;i<arr.length;i++) {
				//j和j+gap进行交换
				for(int j = i-gap;j>=0;j-=gap) {
					if(arr[j]>arr[j+gap]) {
						int temp = arr[j];
						arr[j] = arr[j+gap];
						arr[j+gap] = temp;
					}else {
						break;
					}
				}
			}
		}
	}
}

在这段代码中，我们首先定义了一个待排序的数组arr，然后调用sort方法进行排序。排序完成后，我们使用Arrays.toString方法将排序后的数组转换为字符串并打印出来。

算法分析

希尔排序的时间复杂度为O(n^2)，其中n是数组的长度。这是因为在最坏的情况下，每个元素都需要与所有其他元素进行比较。然而，由于希尔排序在处理部分有序的数组时非常高效，所以它在实际应用中通常比简单的冒泡排序和选择排序要快得多。

结论

希尔排序是一种非常有效的排序算法，特别是对于部分有序的数组。虽然它的平均时间复杂度为O(n^2)，但在实际应用中，由于其优秀的性能，它通常比其他更复杂的排序算法更快。