红黑树浅浅学习

---

红黑树概念

• 二叉树：二叉树是每个节点最多有两个子树的树结构。
• 二叉查找树：又称“二叉搜索树”，左孩子比父节点小，右孩子比父节点大，还有一个特性就是”中序遍历“可以让结点有序。
• 平衡二叉树：它是一颗空树或者它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一颗平衡二叉树。
• 红黑树是一种自平衡的二叉查找树，它属于平衡树，但是却没有平衡二叉树那么“平衡”。可以保证在最坏情况下基本动态操作的时间复杂度为O(log n)。
• 红黑树中的每个节点都有一个颜色属性，可以是红色或黑色。

红黑树满足以下5个性质：

• 每个节点要么是红色的，要么是黑色的，根节点是黑色的。
• 每个叶子节点（NIL节点，空节点）是黑色的。
• 任何相邻节点不能同时为红色。
• 任何叶子节点，到根节点，所经过的黑节点数目相同。
• 当前节点到其所有叶节点包含的黑色节点数量相同。

通过这些性质，红黑树可以保证在插入和删除节点时，自动调整树的结构，以保持树的平衡和性质的满足。相比于普通的二叉查找树，红黑树的平衡性更好，查找、插入和删除都具有更稳定的时间复杂度，因此在很多场景下被广泛应用。

---

红黑树平衡性调整

1. 依次插入 100 90 120，不需要进行平衡性调整
   
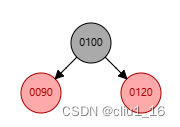
2. 插入85，把90和120变成黑色，100变成红色。但100必须为黑色，100也变成黑色
   

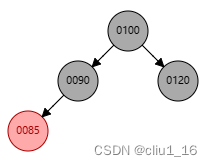
平衡性调整情况1：爷节点为黑色，父节点为红色，且有叔节点为红色，父亲节点为爷节点的左孩子

• 将父节点和叔节点都变为黑色。
• 爷节点变成红色
  • 若爷节点变色之后红黑树性质出现问题，需要沿着爷节点继续向上调整
  • 若爷节点为根节点，要变黑色。

3. 插入60为红色，红黑树继续进行调整，85变成黑色，90变成红色。
   

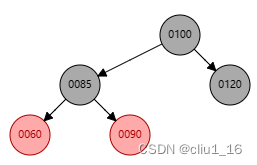
平衡性调整情况2：爷节点为黑色，父节点为红色，没有叔节点或叔节点为黑色，父亲节点为爷节点的左孩子，插入的节点是父节点的左孩子

平衡性调整情况3：爷节点为黑色，父节点为红色，没有叔节点或叔节点为黑色，父亲节点为爷节点的右孩子，插入的节点是父节点的左孩子

平衡性调整情况4-6分别为1-3的反情况

#include <iostream>
#include <list>
#include <vector>
#include <string>
#include <map>
#include <set>
#include <assert.h>
#include <sstream>
#include <stack>

using namespace std;

template<typename T>
struct RBNode{
    T data;
    RBNode* leftChild;
    RBNode* rightChild;
    RBNode* parentNd;

    bool isRed; //判断是否为红色节点。
};

template<typename T>
class RBTree{
public:
    RBTree():root(nullptr){}

    ~RBTree(){
        ReleaseNode(root);
    }

    void InsertElem(const T&e){
        InsertElem(root,e);
    }

    void InsertElem(RBNode<T>*& tNode, const T& e){ //第一个参数类型：指针引用
        RBNode<T>* point = tNode; // 从指向根节点开始
        RBNode<T>* parent = nullptr; // 保存父节点，根节点的父节点先为nullptr

        // 通过一个while循环寻找要插入节点的位置，同时还要把插入路线上所经过的所有节点都保存到栈中，因为这些节点的平衡因子可能要调整。
        while(point !=nullptr){
            if(e==point->data) return; //要插入的数据和当前树中某节点的数据相同，不允许插入
            
            parent = point; // 记录父节点

            if(e > point->data){
                point = point->rightChild;
            }
            else{
                point = point->leftChild;
            }
        }// end while

        // 走到这里，point 等于nullptr，该生成新节点了
        point = new RBNode<T>;
        point->data = e;
        point->leftChild = nullptr;
        point->rightChild = nullptr;
        point->parentNd = nullptr;
        point->isRed = true; //缺省插入的节点先给红色，之后才会判断需不需要进行调整

        if(parent == nullptr){
            // 创建的是根节点
            point->isRed = false;
            tNode = point;
            return;
        } 

        // 创建的不是根节点，要把节点链接到父节点上
        if(e > parent->data){
            parent->rightChild = point;
        }else{
            parent->leftChild = point;
        }

        point->parentNd = parent;
        if(parent->isRed == false) return; //如果父节点是黑色，当前插入的又是红色节点，不需要做什么直接返回

        BalanceTune(point,parent);
        
        // 不管前面经历了什么，根节点固定黑色
        root->isRed = false;

    }

private:

    // 获取兄弟节点指针
    RBNode<T>* getBrotherNode(RBNode<T>* p){
        // 由调用者确认p->parent 一定不为nullptr
        if(p->parentNd->leftChild == p){
            return p->parentNd->rightChild;
        }
        return p->parentNd->leftChild; 
    }


    // 平衡性调整
    void BalanceTune(RBNode<T>* point, RBNode<T>* parent){
        // 能走到这里的，要插入的节点肯定至少在第三层了，因为如果是第二层，那么插入的节点都是红色的，父节点肯定是黑色的

        // 父节点为红色才能走下来(当前节点为红色，此时需要进行平衡性调整)
        RBNode<T>* parentBroNode = nullptr; //叔节点，可能不存在
        RBNode<T>* grandFatherNode = nullptr; //爷节点，因为父节点为红色，红色不能为根，那么至少都是爷节点做根
        
        while(true){
            parentBroNode = (parent->parentNd !=nullptr) ? (getBrotherNode(parent)):nullptr; //叔节点
            grandFatherNode = point->parentNd->parentNd; //爷节点

            // 不断向上调整，爷节点可能有为空的时候
            if(grandFatherNode == nullptr) break;

            // 如果叔节点为红色，那么爷节点不可能为红色
            if(parentBroNode != nullptr && parentBroNode->isRed == true){//平衡性调整情况1，没有将爷节点置为黑色的原因是统一在外部进行根节点为黑色的设置

                // 先处理变色问题
                // (1)父节点和叔节点变为黑色，爷节点变为红色
                parent->isRed = false;
                parentBroNode->isRed = false;
                grandFatherNode->isRed = true;

                // (2)如果爷节点是根，跳出循环，根节点颜色在循环外进行设置为黑色的处理
                if(grandFatherNode == root) break;


                // (3) 往上走继续循环
                point = grandFatherNode;
                parent = point->parentNd;
                if(parent->isRed = false) break;

                continue;
            } 

            // 能走到这里的平衡性调整情况2，不满足if(parentBroNode != nullptr && parentBroNode->isRed == true)
            // 叔节点为黑色或叔节点为空的情况
            // 旋转变色之前的一些信息，这是通用代码
            RBNode<T>* gff = grandFatherNode->parentNd; //太爷节点
            int sign = 0; // 标记1：grandFatherNode是父节点的左孩子，标记2：grandFatherNode是父节点的右孩子。
            if(gff!=nullptr){
                if(gff->leftChild == grandFatherNode){
                    sign = 1;
                }
                else{
                    sign = 2;
                }
            }
            if(grandFatherNode->leftChild == parent){ //第一种情形，父亲是爷节点的左孩子
                // 开始旋转和变色以调整平衡
                if(parent->leftChild == point){ //新节点是父亲节点的左孩子
                    // 右旋转
                    RotateRight(grandFatherNode);
                }else{ //新节点是父亲节点的右孩子
                    // 先左旋后右旋
                    RotateLeftRight(grandFatherNode);
                }

                // 旋转之后变色的代码，通用
                grandFatherNode->isRed = false; //新的根节点设置为黑色
                grandFatherNode->rightChild->isRed = true; //新右叶子设置为红色
            }else{ // 第二种情形，父亲是爷节点的右孩子
                if(parent->rightChild == point){ //新节点是父亲的右孩子
                    RotateLeft(grandFatherNode);
                }else{
                    RotateRightLeft(grandFatherNode);
                }
                // 旋转变色之后的一些公用代码
                grandFatherNode->isRed = false; //新根设置为黑色
                grandFatherNode->leftChild->isRed = true; //新左叶子设置为红色
            }


            //*** 一些通用代码
            // 根已经改变了，所以要设置一些节点指向信息
            if(gff == nullptr){
                root = grandFatherNode;
            }else if(sign == 1){
                gff->leftChild = grandFatherNode;
            }else if(sign == 2){
                gff->rightChild = grandFatherNode;
            }
            break;

        }// end while(true)
        return;
    }

    // 右旋转
    void RotateRight(RBNode<T>*& pointer){ //注意参数类型
        RBNode<T>* ptmproot = pointer;
        pointer = ptmproot->leftChild;
        pointer->parentNd = ptmproot->parentNd;

        ptmproot->leftChild = pointer->rightChild;
        if(pointer->rightChild){
            pointer->rightChild->parentNd =ptmproot;
        }
        pointer->rightChild = ptmproot;
        ptmproot->parentNd = pointer;

    }


    void ReleaseNode(RBNode<T>* pnode){
        if(pnode !=nullptr){
            ReleaseNode(pnode->leftChild);
            ReleaseNode(pnode->rightChild);
        }
        delete pnode;
    }

private:
    RBNode<T>* root; 
};


int main()
{
    RBTree<int> myrbtr;
    int array[] = {80,50,120,30,60,20,40};
    int acount = sizeof(array)/sizeof(int);
    for(int i=0;i<acount;i++){
        myrbtr.InsertElem(array[i]);
    }
    return 0;
}

= =