双指针（普通双指针、对撞指针、快慢指针、滑动窗口）万字
双指针
基本思想
??常见的双指针有四种形式，一种是普通双指针，另?种是对撞指针（直线路段两车相向行驶），还有?种是快慢指针（循环路段两车同向行驶），最后?种是滑动窗口（直线路段两车同向行驶）。
- 普通双指针：?般用于顺序结构中，也称前后指针。
??通过更改或交换两指针的指向状态来实现最终目的。核心：实现两端区域。如关键词：移动、删除、复写 / 修改一个数组。 - 对撞指针：?般用于顺序结构中，也称左右指针。
??核心：两端向中间移动。?个从最左端，另?个从最右端，逐渐往中间逼近。终止条件：?般是两个指针相遇或者错开（循环内部找到结果直接跳出循环 - 可属于优化），即两种 while() 语句判断：- left == right （两指针相撞）
- left > right （两指针错开）
- 快慢指针：?般用于循环结构中，也称龟兔赛跑算法。
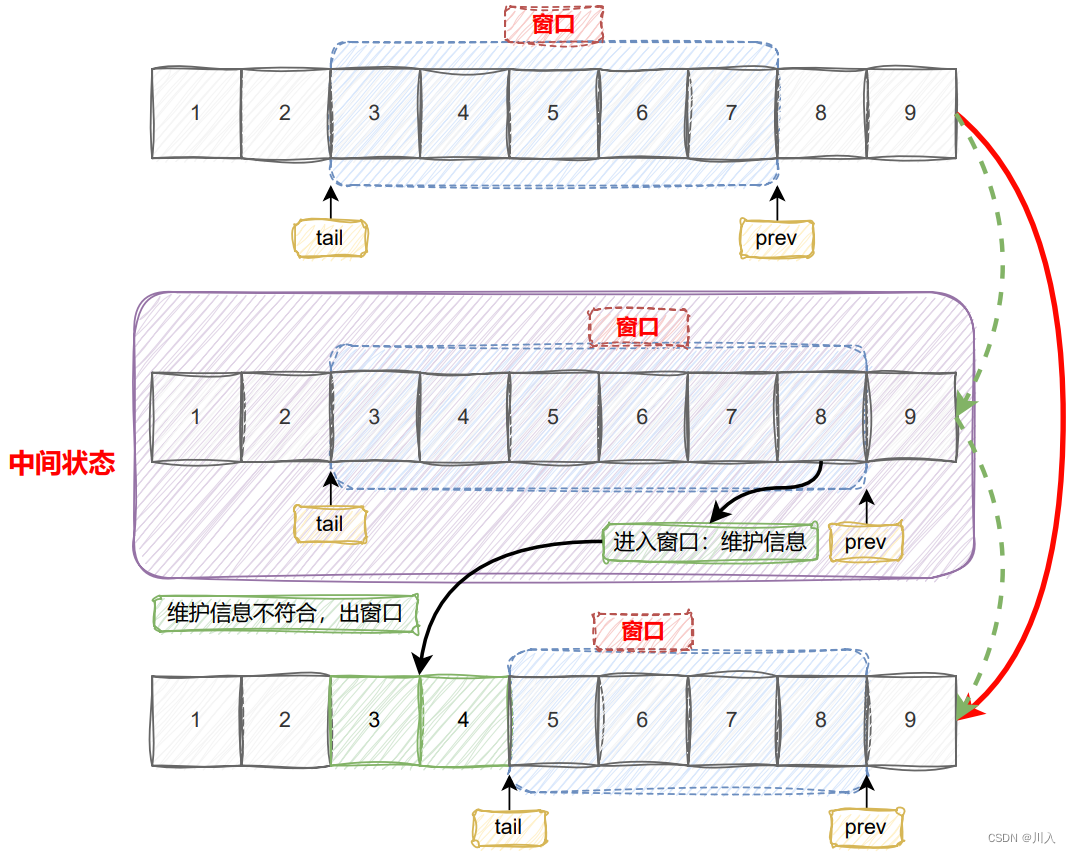
??核心：两个移动速度不同的指针追赶。 研究的问题出现循环往复的情况时，均可尝试考虑使用快慢指针的思想。常见表示形态：慢指针一步，快指针两步。 - 滑动窗口：?般用于顺序结构中，也称特殊同向双指针算法。
??特殊的双指针 -> "同向双指针" -> 滑动窗口，核心：利用单调性。学习过TCP的滑动窗口技术的可以同理之。
此处：略微讲解滑动窗口 - 流量控制机制
入窗口条件：当接收方收到一个数据段时，如果这个数据段的序号在接收窗口内，那么这个数据段就会被接收方接收。出窗口条件：当发送方发送一个数据段时，如果这个数据段的序号在发送窗口内，那么这个数据段就会被发送出去。
引入算法题
初步识别思路???
-
分两块是常见题型，将数组的内容分成左右两部分。这种类型的题：?般就是使用「同向双指针」来解决。- 分两块的另类：处理中
分三块，分为[已被处理区域]，[处理区域]，[等得被处理区域]（比较抽象，下述会有类似题型）删除：首考虑「从前向后」复写/添加：首考虑「从后向前」
- 分两块的另类：处理中
-
单调性是常见题型，数组成递增 / 递减 / 非递增 / 非递减 / 自行sort而成。这种类型的题：?般就是使用「相向双指针」来解决。 -
循环性是常见题型，数组成无限延申 - 存在循环。这种类型的题：?般就是使用「同向快慢双指针」来解决。
算法题
移动零
https://leetcode.cn/problems/move-zeroes/
题目分析：
??将所有 0 移动到数组的末尾 - 利用分两块解题，前部分为非0，后部分为0。需要注意：保持非零元素的相对顺序。使用类型：普通双指针。
解题：
- 区域划分：
cur：从左往右扫描数组，遍历数组。dest：已处理的区间内，非零元素的最后一个位置。
形成：[0, dest] (非0) [dest + 1, cur - 1] (0) [cur, n - 1] (待处理)
class Solution
{
public:
void moveZeroes(vector<int>& nums)
{
for(int cur = 0, dest = -1; cur < nums.size(); cur++)
if(nums[cur]) // 处理?零元素
swap(nums[++dest], nums[cur]);
}
};
??思想同理于快排的前后指针版本。?
void Pointer_QSort(int* a, int begin, int end)
{
assert(a);
// 跳出递归
if (begin >= end)
return;
//keyi:所需要调整的数据下标
int keyi = begin;
int prev, cur;
prev = begin, cur = begin + 1;
while (cur <= end)
{
// cur位置的之小于keyi位置值
//<是升序，>是降序
if (a[cur] < a[keyi] && ++prev != cur)
swap(a[prev], a[cur]);
++cur;
}
swap(a[prev], a[keyi]);
keyi = prev;
//[begin, keyi - 1] keyi [keyi + 1, end]
Pointer_QSort(a, begin, keyi - 1);
Pointer_QSort(a, keyi + 1, end);
}
复写零
链接: https://leetcode.cn/problems/duplicate-zeros/description/
题目分析：算法小心机：正难则反
??此处我们可以发现，如果想正向的解决一个问题是很难的小心机：正难则反。利用分两块解题，反过来看的使用类型：普通双指针。
个人总结：
删除：首考虑「从前向后」复写/添加：首考虑「从后向前」
- 先找到最终结果的最后?个数
（模拟）- 然后对初始从后向前进行操作
（实现）
解题：
- 区域划分：
cur：模拟最后?个数。dest：实现需处理的位置。
形成：[0, cur] (需复写区域) [cur + 1, dest] (无用区域)
class Solution {
public:
void duplicateZeros(vector<int>& arr) {
int cur = -1; // 用于记录模拟最后一个数
int dest = -1; // 用于模拟的推测
int size = arr.size(); // 数组大小
while(dest < size - 1)
{
cur++;
if(arr[cur] == 0)
dest += 2;
else
dest++;
}
// 处理特殊情况 - 由于是0即：dest += 2;
// 是可能会导致dest = size的，从而越界操作。
if(dest == size)
{
arr[dest - 1] = 0;
dest -= 2;
cur--;
}
while(cur >= 0)
{
if(arr[cur] == 0)
{
arr[dest] = 0;
arr[dest - 1] = 0;
dest -= 2;
}
else
{
arr[dest] = arr[cur];
dest--;
}
cur--;
}
}
};
快乐数
链接: https://leetcode.cn/problems/happy-number/
题目分析：
??此处需要一些数学上的分析：鸽巢原理（抽屉原理）
??如3位数的最大值 999 ：
9
2
9^2
92 +
9
2
9^2
92 +
9
2
9^2
92 = 243。也就代表以此方式求244次就必定会有一个重复，因为所得值不可能出现
?
\geqslant
? 999 的情况。
??而如果，只要有 1 的出现就会导致后期全是 1 ，如果重复的不是 1 也就代表不可能到1。利用循环性解题，使用类型：快慢指针。
解题：
class Solution {
public:
int bitsum(int num)
{
if(num == 1)
return 1;
int ret = 0;
while(num)
{
ret += pow(num % 10, 2);
num /= 10;
}
return ret;
}
bool isHappy(int n) {
if(n == 1)
return true;
int fast = bitsum(bitsum(n)), slow = bitsum(n);
while(fast != slow)
{
fast = bitsum(bitsum(fast));
slow = bitsum(slow);
}
return fast == 1;
}
};
盛最多水的容器
链接: https://leetcode.cn/problems/container-with-most-water/description/
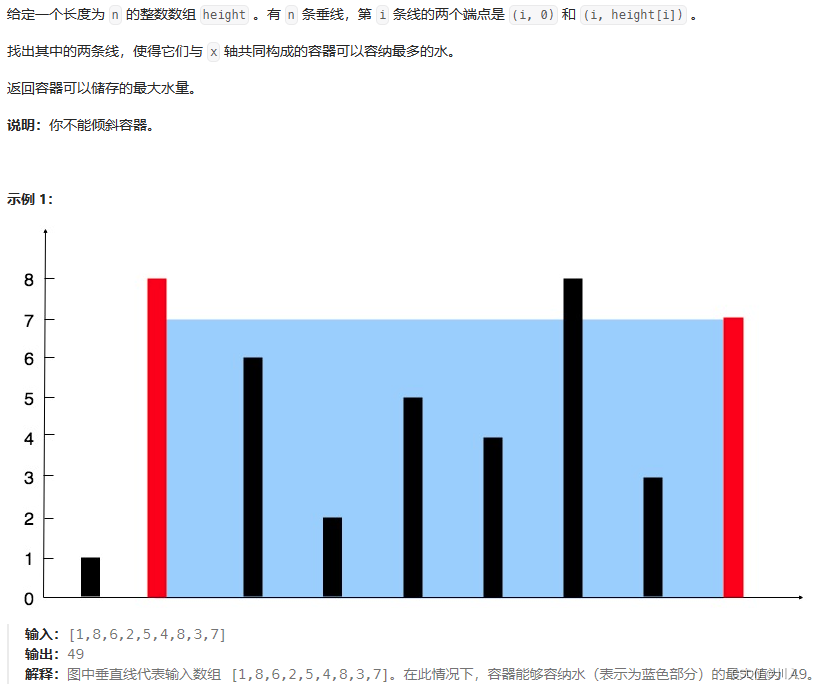
题目分析：
??这个容器的盛水量由 height * wide 决定，利用单调性解题，于是使用类型：对撞指针，因为左 / 右指针向内部移动，必定会导致 wide减小， 那么就一定需要 height 变大，才能保证 盛水量增大 。而根据木桶原理：水的多少取决于最短的木板，所以 height 小的指针移动。
解题：
class Solution {
public:
int maxArea(vector<int>& height)
{
int left = 0, right = height.size() - 1;
int ret = 0;
while(left <= right)
{
int tmp = min(height[left], height[right]) * (right - left);
ret = max(tmp, ret);
if(height[left] > height[right])
{
int tmp_height = height[right--];
while(left <= right && tmp_height > height[right])
right--;
}
else
{
int tmp_height = height[left++];
while(left <= right && tmp_height > height[left])
left++;
}
}
return ret;
}
};
有效三角形的个数
链接: https://leetcode.cn/problems/valid-triangle-number/description/
题目分析：
??本题涉及三角形的特性：a + b > c，所以更加注重的是数值的大小 -> 利用单调性解题，所以此题可运用 sort 排序，实现类型：对撞指针。
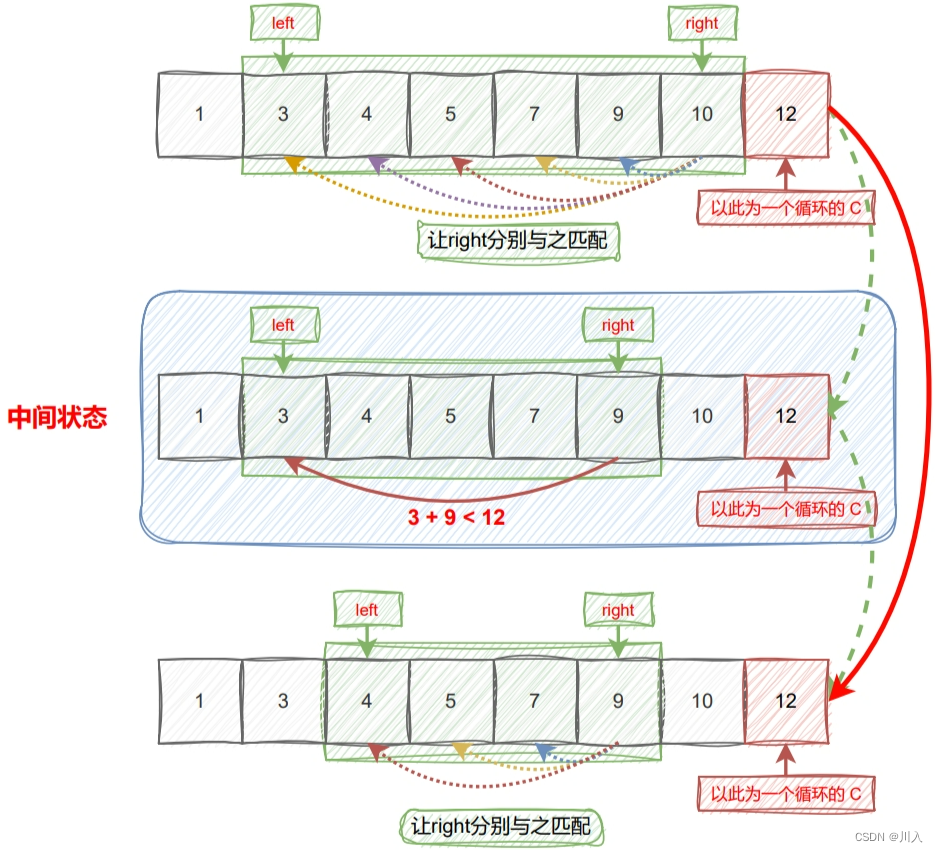
解题：
class Solution {
public:
int triangleNumber(vector<int>& nums) {
sort(nums.begin(), nums.end());
int size = nums.size();
int ret = 0;
for(int cur = size - 1; cur >= 2; cur--)
{
int left = 0, right = cur - 1;
while(left < right)
{
if(nums[left] + nums[right] > nums[cur])
{
ret += right - left;
right--;
}
else
left++;
}
}
return ret;
}
};
查找总价格为目标值的两个商品
链接: https://leetcode.cn/problems/he-wei-sde-liang-ge-shu-zi-lcof/description/
题目分析：
??从题可看出：是按照升序的数组 price，利用单调性解题，首先考虑使用「相向双指针」来解决。使用类型：对撞指针，采取：循环内部找到结果直接跳出循环。
解题：
- 单调性：升序
left++：price [left] 一定增大。right--：price [right] 一定减小。
class Solution {
public:
vector<int> twoSum(vector<int>& price, int target) {
int left = 0, right = price.size() - 1;
while(left < right)
{
if(price[left] + price[right] == target)
return {price[left], price[right]};
else if(price[left] + price[right] < target)
left++;
else
right--;
}
// 对于未指明，随意返回即可
return {-1};
}
};
三数之和
链接: https://leetcode.cn/problems/3sum/description/
题目分析：
??从题可看出：此题于前述有效三角形的个数极其相识，只不过一个的记录条件是 a + b > c，一个是 a + b == c。所以更加注重的是数值的大小 -> 利用单调性解题，所以此题可运用 sort 排序，实现类型：对撞指针。
解题：
?但是要注意的是，这道题里面需要有「去重」操作~
- 找到一个结果之后， left 和 right 指针要「跳过重复」的元素。
- 当使用完一次双指针算法之后， cur 也要「跳过重复」的元素。
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
sort(nums.begin(), nums.end());
vector<vector<int>> ret;
for(int cur = nums.size() - 1; cur >= 2; )
{
int left = 0, right = cur - 1;
while(left < right)
{
if(nums[left] + nums[right] + nums[cur] == 0)
{
ret.push_back({nums[left++], nums[right--], nums[cur]});
while(left < right && nums[left] == nums[left - 1])
left++;
while(left < right && nums[right] == nums[right + 1])
right--;
}
else if(nums[left] + nums[right] + nums[cur] < 0)
left++;
else
right--;
// cout << '1';
}
while(cur >= 2 && nums[cur] == nums[cur - 1])
{
cur--;
}
cur--;
}
return ret;
}
};
滑动窗口
??滑动窗口此算法，极其具有实际意义，所以此处进行强调提出，优化需求一个区域需求O(n)。
利用单调性，规避很多没有必要的枚举行为，必须保证窗口内是合格的。
#时间复杂度：n + n -> O(n)
长度最小的子数组
链接: https://leetcode.cn/problems/minimum-size-subarray-sum/description/
题目分析：
??从题可看出：该题想要一个区域，一个相加和
?
\geqslant
? target 的长度最小的区域，所以此题可运用实现类型：滑动窗口。
解题：
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums)
{
int prev = 0, tail = 0; // 窗口区域
int sum = 0; // 窗口内部所维护的条件
int ret = INT_MAX;
while(prev < nums.size())
{
// 进入窗口, 维护窗口条件
sum += nums[prev];
// 窗口条件是否合格
if(sum >= target)
{
while(sum >= target)
sum -= nums[tail++]; // 出窗口
ret = min(ret, prev - tail + 1 + 1);
}
prev++;
}
if(ret == INT_MAX)
return 0;
return ret;
}
};
无重复字符的最长子串
链接: https://leetcode.cn/problems/longest-substring-without-repeating-characters/description/
题目分析：
??从题可看出：该题想要一个区域，一个不含有重复字符的最长区域，所以此题可运用实现类型：滑动窗口。
解题：
class Solution {
public:
int lengthOfLongestSubstring(string s)
{
vector<int> hash(256 , 0);
int prev = 0, tail = 0;
int ret = 0;
while(prev < s.size())
{
// 入窗口 - 维护窗口条件
hash[s[prev]]++;
while(hash[s[prev]] > 1)
{
hash[s[tail]]--; // 出窗口
tail++;
}
ret = max(ret, prev - tail + 1);
prev++;
}
return ret;
}
};
将x减到0的最小操作数
链接: https://leetcode.cn/problems/minimum-operations-to-reduce-x-to-zero/description/
题目分析：
??这个题是一个有意思的题，如果想利用类型：滑动窗口解题，我们需要进行一个转换，即滑动窗口需要核心：维护窗口的条件（一段区域的条件），可以说就是子数组的状态，但是此题是从两端取就是不从中间取，那我们进行转换。
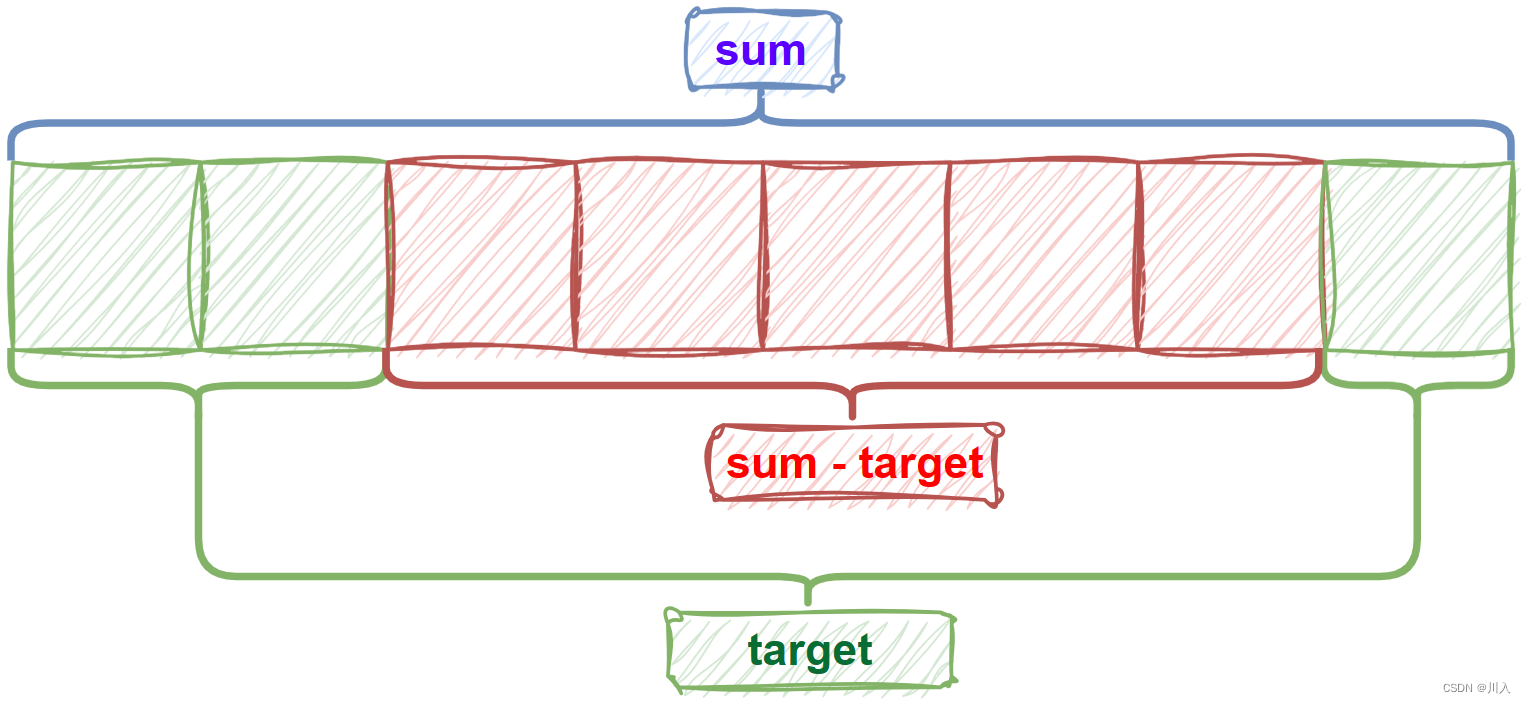
???类型：滑动窗口，针对的是一个区间。
解题：
class Solution {
public:
int minOperations(vector<int>& nums, int x) {
// 推测窗口条件
int sum = 0;
int size = nums.size();
for(auto val : nums)
{
sum += val;
}
int condition = sum - x; // 新窗口条件
// 滑动窗口算法
int tail = 0, prev = 0;
int ret = INT_MAX;
int tmp_sum = 0;
while(prev < size)
{
// 进入窗口, 维护窗口条件
tmp_sum += nums[prev];
while(tail <= prev && tmp_sum > condition)
{
tmp_sum -= nums[tail];
tail++;
}
if(tmp_sum == condition)
ret = min(ret, size - (prev - tail + 1));
prev++;
}
if(ret == INT_MAX)
return -1;
return ret;
}
};
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码（1）
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 嵌入式热门发展方向有哪些?
- TiDB 7.1 多租户在中泰证券中的应用
- 后处理：Calibration Method
- 怎么画业务流程图？掌握这几步就够了
- 初学dfs深度优先搜索&洛谷【 八皇后 Checker Challenge】题解
- Qt中图片旋转缩放操作
- Linux 文本内容处理小记
- JAVA-集合
- layui框架实战案例(25):table组件筛选列记忆功能
- 数字频率合成器dds的量化性能分析matlab仿真