2024/1/21周报
文章目录
摘要
本周阅读了一篇基于LSTM的深度学习模型用于长期旅游需求预测的文章,作者所提出的预测模型是基于长短期记忆网络(LSTM),它能够整合来自外生变量的数据。通过希腊三家酒店真实的数据的评估,结果表明,与所有三家酒店的知名国家的最先进的方法相比,所提出的模型的上级预测性能。此外,还对GRU进行推导和代码实现。
Abstract
This week, an article about the application of LSTM-based deep learning model to long-term tourism demand forecasting is readed. The forecasting model proposed by the author is based on long-term and short-term memory network (LSTM), which can integrate data from exogenous variables. Through the evaluation of real data of three hotels in Greece, the results show that the superior prediction performance of the proposed model is better than that of the most advanced methods in famous countries of all three hotels. In addition, GRU is deduced and implemented by code.
文献阅读
题目
LSTM-Based Deep Learning Models for Long-Term Tourism Demand Forecasting
问题与创新
旅游需求预测是整个旅游需求管理过程中的一项重要任务,因为它可以做出明智的决策,从而增加酒店的收入。
已有的相关文献中提出的旅游需求预测模型大多侧重于短期预测。然而,有效规划和管理旅游部门的企业需要长期预测。长期预测被认为是一项更困难的任务,因为它会引入误差积累和计算复杂性增加等问题。
作者通过引入深度学习模型进行长期旅游需求预测来填补相关文献中的上述空白的第一步。所提出的深度学习架构基于LSTM,并结合气象资料进行旅游预测。
主要贡献如下:
1.开发新的深度学习模型,用于准确的长期旅游需求预测,无论是否有外生变量(即天气数据);
2.调查外生变量对预测准确性的影响,特别是深度学习模型的性能;
3.使用真实世界的旅游相关数据和天气数据对所提出的模型进行评估的彻底实验过程。
方法
RNN网络
RNN中的节点除了当前时刻的典型信号外,还将其前一时刻的状态作为输入。隐藏节点h在时刻t的输出 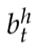 由以下等式给出:
由以下等式给出:
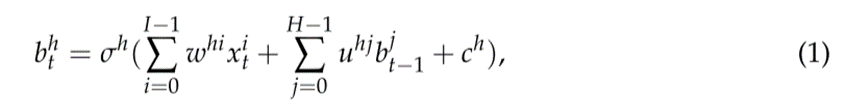
RNN用于识别数据序列(或系列)中的模式,例如文本,基因组,声音信号,数字时间序列等。
LSTM网络

LSTM网络是一种RNN架构,它通过允许梯度在网络中反向传播而克服了消失梯度问题。一个常见的LSTM架构由一个单元(LSTM的内存)和三个控制LSTM内部信息流的门组成。具体来说,输入门控制新值流入单元的程度,遗忘门控制值保留到单元的程度,输出门控制单元中的值用于计算LSTM输出的程度。
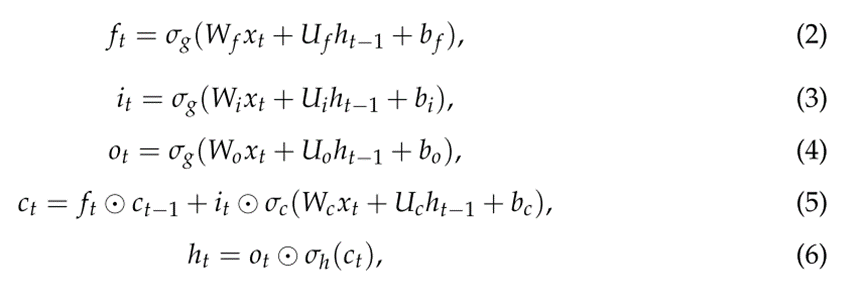
LSTM网络的单元使用sigmoids上的元素操作来决定存储什么和留下什么,sigmoids是可微的,因此适合于反向传播。
目标变量与外部变量的相关性
作者建立了一个模型,除了旅游相关数据外,还集成了天气数据。使用了皮尔逊积差相关系数(PPMCC)估计旅游变量(即,房间预订数量)和天气变量,来确定哪些天气变量对预测目标更有用。PPMCC如下所示:
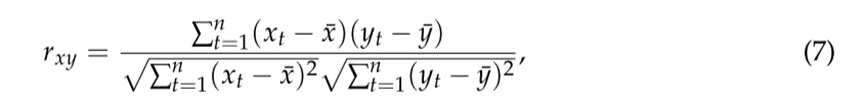
实验
数据集
为了评估建议和基准旅游需求预测模型,使用了来自希腊三家酒店的真实旅游需求数据。特别是,所使用的数据集包含希腊三家不同酒店在过去旅游季节的每一天的客房预订记录。出于数据隐私的考虑,作者使用Hotel A、Hotel B和Hotel C代指三家酒店。
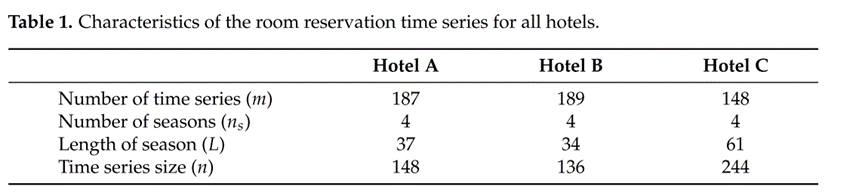
评估准则
为了衡量所提出的模型和基准模型的预测性能,使用了旅游需求预测文献中广泛使用的两个预测误差指标,即均方根误差(RMSE)和平均绝对百分比误差(MAPE):

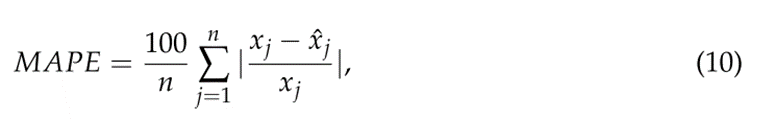
参数设置
作者使用的普通LSTMB与融合天气变量的LSTMX超参数值分别总结在表3和表4中:
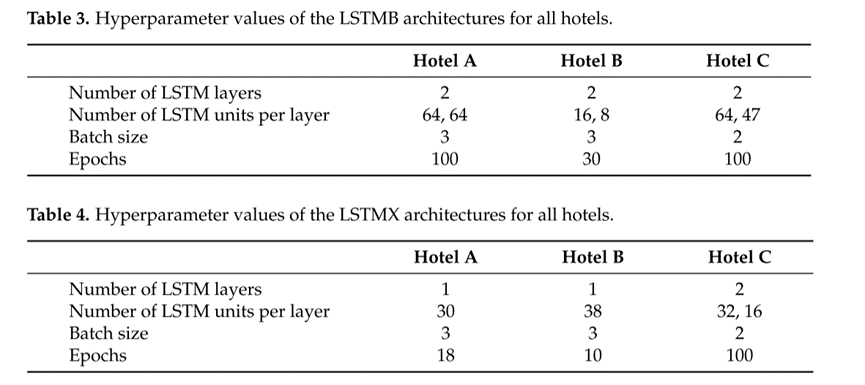
实验结果
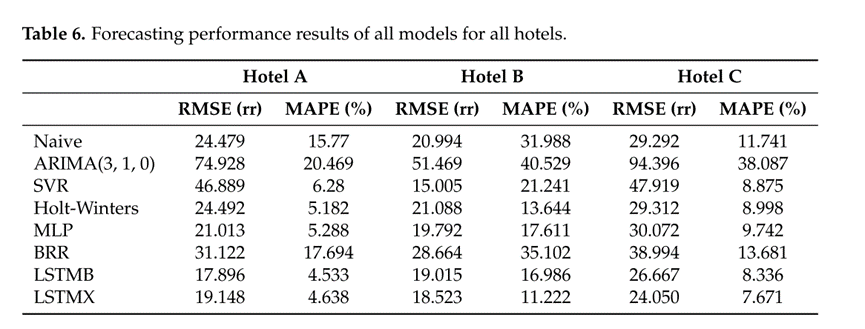
所提出的模型实现更好的预测性能在所有情况下相比,广泛用于旅游需求预测的六个不同的基准模型。此外,作者验证了假设,即来自外生变量(例如,天气数据),用于长期旅游需求预测的基础深度学习架构,可以显着提高其性能。
深度学习
GRU
网络结构介绍
GRU神经网络的整体结构与RNN神经网络的整体结构相同,区别在于GRU神经网络中的隐藏层单元引入了门控单元,其具体的结构如下图所示:
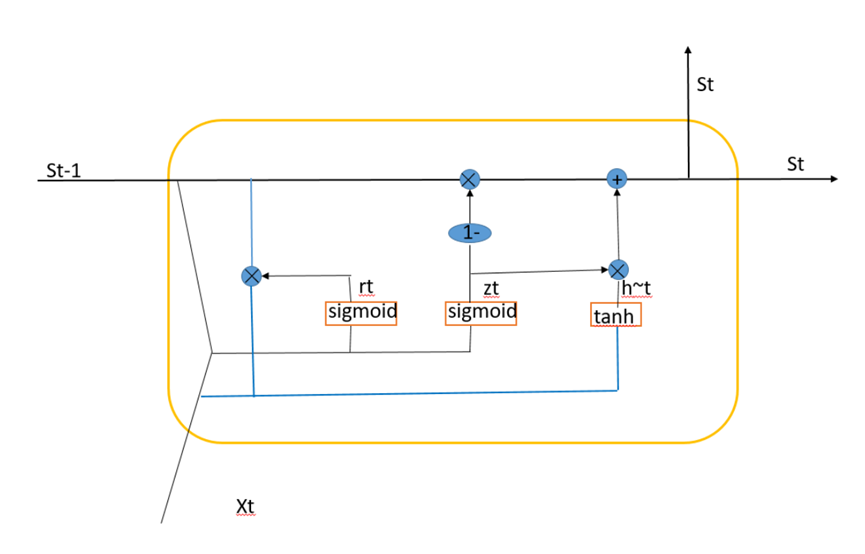
前向传播过程

传递参数:

前向传播的代码实现
#encoding=utf-8
import numpy as np
def sigmoid(x):
return 1/(1 + np.exp(-x))
def tanh(x):
class GRUCell:
def __init__(self,W_r,W_z,W_hh,U_r,U_z,U_hh,W_o,br,bz,bh,bo):
self.W_r = W_r
self.W_z = W_z
self.W_hh = W_hh
self.U_r = U_r
self.U_z = U_z
self.U_hh = U_hh
self.W_o = W_o
self.br = br
self.bz = bz
self.bh = bh
self.bo = bo
def forward(self,X,S_prev):
net_rt = np.dot(self.W_r.T,X)+np.dot(self.U_r,S_prev) + br
rt = sigmoid(net_rt)
net_zt = np.dot(self.W_z.T,X)+ np.dot(self.U_z,S_prev) + bz
zt = sigmoid(net_zt)
net_hht = np.dot(self.W_hh.T,X) + np.dot(self.U_hh.T,(rt * S_prev) + bh)
hht = np.tanh(net_hht)
St = (1 - zt) * S_prev + z(t) * hht
net_ot = np.dot(self.W_o.T,St) + bo
Ot = sigmoid(net_ot)
return net_rt,rt,net_zt,zt,net_hht,hht,St,net_ot,Ot
反向传播过程
首先分别计算误差关于nethh(t)、netz(t)、netr(t)、St-1的梯度运算,误差选用softmax函数交叉熵计算。



权重参数求导如下:

在更新的时候,需要将所有的时刻的导数进行累加。以Wr为例,则最终更新公式为:

在设计GRU网络的时候,可能在最后的时刻才会有输出,此时,对于Wo,Bo的更新不需要按照时刻进行累加的过程。如果每一个时刻都有输出,则需要进行累加之后,进行更新。
简单的GRU代码实现
import torch
import torch.nn as nn
lstm_layer = nn.LSTM(3,5) #输入特征为3,隐含特征为5的特征量
gru_layer = nn.GRU(3,5) #同样的隐含大小
sum(p.numel() for p in lstm_layer.paramenters()) #计算lstm总参数量,调用paramenters()函数,在对其进行参数枚举(p代表参数),p.numel()计算每个参数p的所有元素进行统计----》200
sum(p.numel() for p in gru_layer.paramenters()) ----->150
## GRU的参数量是LSTM的0.75
#准备工作
def gru_forward(input, initial_states, w_ih, w_hh, b_ih, b_hh): #定义函数,前向运算 initial_states提供初始状态 w权重--表示大的矩阵 b_ih偏置项
prev_h = initial_states #h t=0时刻的初始值
bs, T, i_size = input.shape #对input进行拆解
h_size = w_ih.shape[0] // 3 #公式里每一个 h_size(隐含神经元个数) 配三个权重
#计算公式里的W ---由于目前提供的w是二维张量,而input和initial_states都是三维张量(带有batch这个维度)-----》对两个w进行扩充维度
#对权重扩维,复制成batch_size倍
batch_w_ih = w_ih.unsqueeze(0).tile(bs,1,1) #从第0维起扩一维,tile(bs,1,1)复制一下,第一维扩大到bs倍,其他保持不变
batch_w_hh = w_hh.unsqueeze(0).tile(bs,1,1)
output = torch.zeros(bs, T, h_size) #对输出初始化 GRU网络的输出状态序列
#计算
for t in range(T): #for循环对每一时刻进行迭代更新
x=input(:,t,:) #step1:找到当前时刻的输入 t时刻GRU cell的输入特征向量,大小为[bs,i_size]
w_time_x = torch.bmm(batch_w_ih, x.unsqueeze(-1)) #扩成3维---[bs,3*h_size,1]
w_time_x = w_time_x.squeeze(-1) #.squeeze(-1)去掉维度为1的维度---[bs,3*h_size]
w_time_h_prev = torch.bmm(batch_w_hh, prev_h.unsqueeze(-1))
w_time_h_prev = w_time_h_prev.squeeze(-1)
#计算重置门和更新门
r_t = torch.sigmoid(w_time_x[:, :h_size]+w_time_h_prev[:, :h_size]+b_ih[:h_size]+b_hh[:h_size])
z_t = torch.sigmoid(w_time_x[:, h_size:2*h_size]+w_time_h_prev[:, h_size:2*h_size]+b_ih[h_size:2*h_size]+b_hh[h_size:2*h_size])
#计算候选状态nt
n_t = torch.tanh(w_time_x[:, 2*h_size:3*h_size]+b_ih[2*h_size:3*h_size]+\
r_t*(w_time_h_prev[:,2*h_size:3*h_size]+b_hh[2*h_size:3*h_size])) #候选状态
prev_h = (1-z_t)*n_t+z_t*prev_h #增量更新得到当前时刻最新隐含状态
output[:, t, :] = prev_h #把 prev_h 喂入到output矩阵中
return output, prev_h
#测试函数的正确性--用pytprch的官方api测试
bs, T, i_size, h_size = 2, 3, 4, 5
input = torch.randn(bs, T, i_size) #输入序列
h0 = torch.randn(bs, h_size) #初始值,不需要训练
#定义GRU量 调用官方GRU API
gru_layer = nn.GRU(i_size, h_size ,batch_first=True)
output, h_final = gru_layer(input, h0.unsqueeze(0))
print(output)
for k, v in gru_layer.named_parameters():
print(k, v.shape)
#调用自定义的gru_forward函数
output_custom, h_final_custom = gru_forward(input,h0,gru_layer.weight_ih_10,gru_layer.weight_hh_10,gru_layer.bias_ih_10,gru_layer.bias_hh_10)
print(torch.allclose(output,output_custom)) #allclose对比两个浮点型张量是否非常接近
print(torch.allclose(h_final,h_final_custom_custom))
总结
本周对GRU的数学原理进行推导和补充学习,GRU也是基于RNN结构,并对LSTM进行简化。值得注意的是,GRU和LSTM适用于不同的场景,GRU训练速度要快于LSTM。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 极智芯 | 解读自动驾驶芯片之寒武纪行歌SD系列
- Shell脚本①编程规范与脚本基础
- 【GitHub项目推荐--不错的 React 开源项目】【转载】
- Go并发读写文件、分片写、分片下载文件(实用版)
- 【书生·浦语大模型实战营03】《基于 InternLM 和 LangChain 搭建你的知识库》学习笔记
- English: words used for emphasis
- 大数据Doris(四):直接编译(CentOS/Ubuntu)准备
- Export Spreadsheets to CSV WinForms App -Spread.NET
- eNSP小实验--实现全网互通
- Leveraging Unlabeled Data for Crowd Counting by Learning to Rank