《剑指 Offer》专项突破版 - 面试题 24、25、26 和 27 : 详解如何反转链表，以及如何利用反转链表来解决典型的算法面试题（C++ 实现）

目录

前言

一、反转链表

1.1 - 方法一

1.2 - 方法二

二、链表中的数字相加

三、重排链表

四、回文链表

---

?

---

前言

单向链表的最大特点就是其单向性，只能顺着指向下一个节点的指针方向从头到尾遍历链表而不能反向遍历。这种特性用一句古诗来形容正合适：黄河之水天上来，奔流到海不复回。

有些面试题只有从链表尾节点开始遍历到头节点才容易解决。这个时候可以先将链表反转，然后在反转的链表中从头到尾遍历，这就相当于在原来的链表中从尾到头遍历。

下面介绍如何反转链表，以及如何利用反转链表来解决典型的算法面试题。

---

一、反转链表

题目：

定义一个函数，输入一个链表的头节点，反转该链表并输出反转后链表的头节点。例如，把下图 (a) 中的链表反转之后得到的链表如下图 (b) 所示。

1.1 - 方法一

class Solution {
public:
 ? ?ListNode* reverseList(ListNode* head) {
 ? ? ? ?ListNode* prev = nullptr;
 ? ? ? ?ListNode* cur = head;
 ? ? ? ?while (cur)
 ? ? ?  {
 ? ? ? ? ? ?ListNode* next = cur->next;
 ? ? ? ? ? ?cur->next = prev;
 ? ? ? ? ? ?prev = cur;
 ? ? ? ? ? ?cur = next;
 ? ? ?  }
 ? ? ? ?return prev;
 ?  }
};

1.2 - 方法二

从头到尾遍历原始链表，将链表中的节点依次头插到新链表中。

class Solution {
public:
 ? ?ListNode* reverseList(ListNode* head) {
 ? ? ? ?ListNode* reversedHead = nullptr;
 ? ? ? ?ListNode* cur = head;
 ? ? ? ?while (cur)
 ? ? ?  {
 ? ? ? ? ? ?ListNode* next = cur->next;
 ? ? ? ? ? ?cur->next = reversedHead;
 ? ? ? ? ? ?reversedHead = cur;
 ? ? ? ? ? ?cur = next;
 ? ? ?  }
 ? ? ? ?return reversedHead;
 ?  }
};

---

二、链表中的数字相加

题目：

给定两个表示非负整数的单向链表，请问如何实现这两个整数的相加并且把它们的和仍然用单向链表表示？链表中的每个节点表示整数十进制的一位，并且头节点对应整数的最高位数而尾节点对应整数的个数位。

分析：

这是一个看起来很简单的题目。很多应聘者的第一反应是根据链表求出整数，然后直接将两个整数相加，最后把结果用链表表示。这种思路的最大问题是没有考虑整数有可能溢出。当链表较长时，表示的整数很大，可能会超出 int 甚至 long 的范围，如果根据链表求出整数就可能会溢出。

通常两个整数相加都是先加个位数，再加十位数，然后依次相加更高位数字，所以不能从两个链表的头节点开始相加，而是应该把它们的尾节点对齐并把对应的数位相加。因此，首先应该反转这两个表示非负整数的单向链表，反转之后的链表的头节点表示个位数，尾节点表示最高位数。此时从两个链表的头节点开始相加，就相当于从整数的个位数开始相加。

然后，在做加法时还需要注意的是进位。如果两个整数的个位数相加的和超过 10，就会往十位数产生一个进位。下一步做十位数相加时就要把这个进位考虑进去。

下图总结了用链表表示的两个整数 984 和 18 相加的过程。

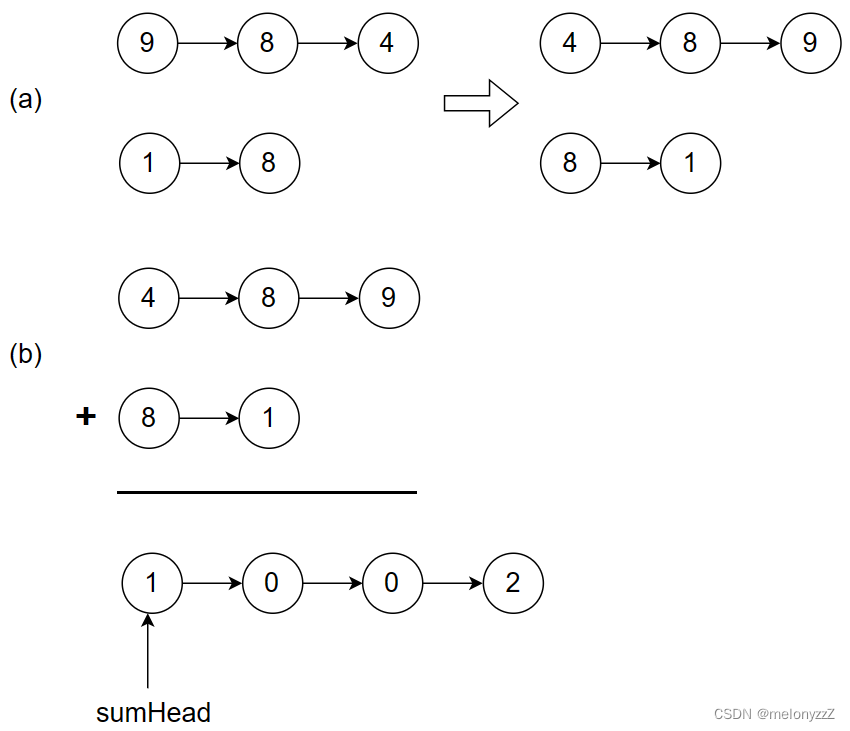
代码实现：

class Solution {
public:
 ? ?ListNode* reverseList(ListNode* head) {
 ? ? ? ?ListNode* prev = nullptr;
 ? ? ? ?ListNode* cur = head;
 ? ? ? ?while (cur)
 ? ? ?  {
 ? ? ? ? ? ?ListNode* next = cur->next;
 ? ? ? ? ? ?cur->next = prev;
 ? ? ? ? ? ?prev = cur;
 ? ? ? ? ? ?cur = next;
 ? ? ?  }
 ? ? ? ?return prev;
 ?  }
?
 ? ?ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
 ? ? ? ?l1 = reverseList(l1);
 ? ? ? ?l2 = reverseList(l2);
 ? ? ? ?ListNode* sumHead = nullptr;
 ? ? ? ?int carry = 0;
 ? ? ? ?while (l1 || l2 || carry)
 ? ? ?  {
 ? ? ? ? ? ?int sum = 0;
 ? ? ? ? ? ?if (l1)
 ? ? ? ? ?  {
 ? ? ? ? ? ? ? ?sum += l1->val;
 ? ? ? ? ? ? ? ?l1 = l1->next;
 ? ? ? ? ?  }
 ? ? ? ? ? ?if (l2)
 ? ? ? ? ?  {
 ? ? ? ? ? ? ? ?sum += l2->val;
 ? ? ? ? ? ? ? ?l2 = l2->next;
 ? ? ? ? ?  }
 ? ? ? ? ? ?sum += carry;
?
 ? ? ? ? ? ?ListNode* newNode = new ListNode(sum % 10);
 ? ? ? ? ? ?carry = sum / 10;
?
 ? ? ? ? ? ?// 头插
 ? ? ? ? ? ?newNode->next = sumHead;
 ? ? ? ? ? ?sumHead = newNode;
 ? ? ?  }
 ? ? ? ?return sumHead;
 ?  }
};

---

三、重排链表

题目：

给定一个链表，链表中节点的顺序是 ，请问如何重排链表使节点的顺序变成 ？例如，输入下图 (a) 中的链表，重排之后的链表如下图 (b) 所示。

分析：

如果仔细观察输入链表和输出链表之间的联系，就能发现重排链表其实包含以下几个操作：

1. 首先把链表分成前后两半。在示例链表中，前半段链表包含 1、2、3 这三个节点，后半段链表包含 4、5、6 这三个节点。

   可以使用一快一慢双指针来寻找链表的中间节点。快的指针一次顺着 next 指针向前走两步，而慢的指针一次只走一步。

   如果链表的节点总数为偶数，那么当快指针走到链表的尾节点时，慢指针正好走到前半段链表的最后一个节点，前半段链表和后半段链表的节点个数相同。

   如果链表的节点总数为奇数，那么当快指针走到空时，慢指针正好走到前半段链表的最后一个节点，前半段链表比后半段链表多一个节点。

2. 然后把后半段链表反转。示例链表的后半段链表反转之后，节点的顺序变成 6、5、4。

3. 最后从前半段链表和后半段链表的头节点开始，逐个把它们的节点连接起来形成一个新的链表。先把前半段链表和后半段链表的头节点 1 和 6 连接起来，再把处在第 2 个位置的节点 2 和 5 连接起来，最后把两个尾节点 3 和 4 连接起来，因此在新的链表中节点的顺序是 1、6、2、5、3、4。

代码实现：

class Solution {
public:
 ? ?ListNode* reverseList(ListNode* head) {
 ? ? ? ?ListNode* prev = nullptr;
 ? ? ? ?ListNode* cur = head;
 ? ? ? ?while (cur)
 ? ? ?  {
 ? ? ? ? ? ?ListNode* next = cur->next;
 ? ? ? ? ? ?cur->next = prev;
 ? ? ? ? ? ?prev = cur;
 ? ? ? ? ? ?cur = next;
 ? ? ?  }
 ? ? ? ?return prev;
 ?  }
?
 ? ?void reorderList(ListNode* head) {
 ? ? ? ?if (head == nullptr)
 ? ? ? ? ? ?return;
?
 ? ? ? ?ListNode* slow = head;
 ? ? ? ?ListNode* fast = head->next;
 ? ? ? ?while (fast && fast->next)
 ? ? ?  {
 ? ? ? ? ? ?slow = slow->next;
 ? ? ? ? ? ?fast = fast->next->next;
 ? ? ?  }
?
 ? ? ? ?ListNode* rightCur = reverseList(slow->next);
 ? ? ? ?slow->next = nullptr;
?
 ? ? ? ?ListNode* leftCur = head;
 ? ? ? ?while (rightCur)
 ? ? ?  {
 ? ? ? ? ? ?ListNode* leftNext = leftCur->next;
 ? ? ? ? ? ?ListNode* rightNext = rightCur->next;
 ? ? ? ? ? ?leftCur->next = rightCur;
 ? ? ? ? ? ?rightCur->next = leftNext;
 ? ? ? ? ? ?leftCur = leftNext;
 ? ? ? ? ? ?rightCur = rightNext;
 ? ? ?  }
 ?  }
};

---

四、回文链表

题目：

如何判断一个链表是不是回文？要求解法的时间复杂度是 O(n)，并且不得使用超过 O(1) 的辅助空间。如果一个链表是回文，那么链表的节点序列从前往后看和从后往前看是相同的。例如，下图中的链表的节点序列从前往后看和从后往前看都是 1、2、3、3、2、1，因此这是一个回文链表。

分析：

如果不考虑辅助空间的限制，直观的解法是创建一个新的链表，链表中节点的顺序和输入链表的节点顺序正好相反。如果新的链表和输入链表是相同的，那么输入链表就是一个回文链表。只是这种解法需要创建一个和输入链表长度相等的链表，因此需要 O(n) 的辅助空间。

仔细分析回文链表的特点以便找出更好的解法。回文链表的一个特性是对称性，也就是说，如果把链表分为前后两半，那么前半段链表反转之后与后半段链表是相同的。在上图所示的包含 6 个节点的链表中，前半段链表的 3 个节点反转之后分别是 3、2、1，后半段链表的 3 个节点也分别是 3、2、1，因此它是一个回文链表。

上图所示的链表的节点总数是偶数。如果链表的节点总数是奇数，那么把链表分为前后两半时不用包括中间节点。例如，一个链表中的节点顺序是 1、2、k、2、1，前面两个节点反转之后是 2、1，后面两个节点也是 2、1，不管中间节点的值是什么该链表都是回文链表。

代码实现：

class Solution {
public:
 ? ?ListNode* reverseList(ListNode* head) {
 ? ? ? ?ListNode* prev = nullptr;
 ? ? ? ?ListNode* cur = head;
 ? ? ? ?while (cur)
 ? ? ?  {
 ? ? ? ? ? ?ListNode* next = cur->next;
 ? ? ? ? ? ?cur->next = prev;
 ? ? ? ? ? ?prev = cur;
 ? ? ? ? ? ?cur = next;
 ? ? ?  }
 ? ? ? ?return prev;
 ?  }
?
 ? ?bool isPalindrome(ListNode* head) {
 ? ? ? ?if (head == nullptr || head->next == nullptr)
 ? ? ? ? ? ?return true;
 ? ? ? ?
 ? ? ? ?ListNode* slow = head;
 ? ? ? ?ListNode* fast = head->next;
 ? ? ? ?while (fast->next && fast->next->next)
 ? ? ?  {
 ? ? ? ? ? ?slow = slow->next;
 ? ? ? ? ? ?fast = fast->next->next;
 ? ? ?  } 
?
 ? ? ? ?ListNode* rightCur = slow->next;
 ? ? ? ?if (fast->next) ?// 链表的节点总数是奇数
 ? ? ? ? ? ?rightCur = slow->next->next;
 ? ? ? ?
 ? ? ? ?slow->next = nullptr;
 ? ? ? ?ListNode* leftCur = reverseList(head);
 ? ? ? ?while (leftCur && rightCur)
 ? ? ?  {
 ? ? ? ? ? ?if (leftCur->val != rightCur->val)
 ? ? ? ? ? ? ? ?return false;
?
 ? ? ? ? ? ?leftCur = leftCur->next;
 ? ? ? ? ? ?rightCur = rightCur->next;
 ? ? ?  }
 ? ? ? ?return true;
 ?  }
};