leetcode - 1901. Find a Peak Element II
Description
A peak element in a 2D grid is an element that is strictly greater than all of its adjacent neighbors to the left, right, top, and bottom.
Given a 0-indexed m x n matrix mat where no two adjacent cells are equal, find any peak element mat[i][j] and return the length 2 array [i,j].
You may assume that the entire matrix is surrounded by an outer perimeter with the value -1 in each cell.
You must write an algorithm that runs in O(m log(n)) or O(n log(m)) time.
Example 1:
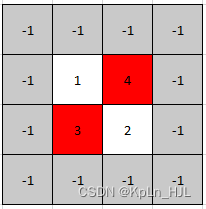
Input: mat = [[1,4],[3,2]]
Output: [0,1]
Explanation: Both 3 and 4 are peak elements so [1,0] and [0,1] are both acceptable answers.
Example 2:
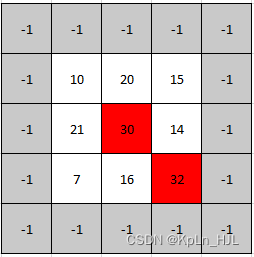
Input: mat = [[10,20,15],[21,30,14],[7,16,32]]
Output: [1,1]
Explanation: Both 30 and 32 are peak elements so [1,1] and [2,2] are both acceptable answers.
Constraints:
m == mat.length
n == mat[i].length
1 <= m, n <= 500
1 <= mat[i][j] <= 105
No two adjacent cells are equal.
Solution
o ( m ? n ) o(m*n) o(m?n) time compleixty
Find the maximum of each column or row, and find the peak element of those maximum elements.
Time complexity: o ( m ? n ) o(m*n) o(m?n) for finding the maximum elements, n log ? m ) n\log m) nlogm) for finding the peak element.
o ( n log ? m ) o(n\log m) o(nlogm) time complexity
We don’t need to calculate the maximum of each row, instead we just need to know the maximum of midRow, and compare it with the adjacent rows. discard the smaller half.
By doing this, we could make sure we find the globally peak.
Time complexity:
o
(
n
log
?
m
)
o(n\log m)
o(nlogm)
Space complexity:
o
(
1
)
o(1)
o(1)
Code
o ( m ? n ) o(m*n) o(m?n) time compleixty
class Solution:
def findPeakGrid(self, mat: List[List[int]]) -> List[int]:
m, n = len(mat), len(mat[0])
candidates = []
for i in range(m):
cur_max = -1
cur_max_index = -1
for j in range(n):
if mat[i][j] > cur_max:
cur_max = mat[i][j]
cur_max_index = j
candidates.append((cur_max, cur_max_index))
left, right = 0, len(candidates) - 1
while left < right:
mid = (left + right) >> 1
if (mid - 1 < 0 or candidates[mid - 1][0] < candidates[mid][0]) and (mid + 1 >= len(candidates) or candidates[mid + 1][0] < candidates[mid][0]):
return [mid, candidates[mid][1]]
elif mid - 1 < 0 or candidates[mid - 1][0] < candidates[mid][0]:
left = mid + 1
elif mid + 1 >= len(candidates) or candidates[mid + 1][0] < candidates[mid][0]:
right = mid
else:
left = mid + 1
mid = (left + right) >> 1
return [mid, candidates[mid][1]]
o ( n log ? m ) o(n\log m) o(nlogm) time complexity
class Solution:
def findPeakGrid(self, mat: List[List[int]]) -> List[int]:
m, n = len(mat), len(mat[0])
left, right = 0, m - 1
while left < right:
mid = (left + right) >> 1
# find maximum on midth row
cur_max, cur_max_index = -1, -1
for col in range(0, n):
if mat[mid][col] > cur_max:
cur_max = mat[mid][col]
cur_max_index = col
if (mid - 1 < 0 or mat[mid - 1][cur_max_index] < mat[mid][cur_max_index]) and (mid + 1 >= m or mat[mid + 1][cur_max_index] < mat[mid][cur_max_index]):
return [mid, cur_max_index]
elif mid - 1 < 0 or mat[mid - 1][cur_max_index] < mat[mid][cur_max_index]:
left = mid + 1
elif mid + 1 >= m or mat[mid + 1][cur_max_index] < mat[mid][cur_max_index]:
right = mid
else:
left = mid + 1
mid = (left + right) >> 1
# find maximum on midth row
cur_max, cur_max_index = -1, -1
for col in range(0, n):
if mat[mid][col] > cur_max:
cur_max = mat[mid][col]
cur_max_index = col
return [(left + right) >> 1, cur_max_index]
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Adobe软件打开后设置默认页面方式和默认鼠标方式
- 数据结构与算法-第八章 排序技术
- 你也是爬虫高手?毫秒级抢票,光速入监狱
- 【Spring】Spring AOP
- 在word文档中插入Latex格式的公式
- 如何在Linux上搭建本地Docker Registry并实现远程连接
- error LNK2001: unresolved external symbol memset
- 计算机网络——数据链路层(1)
- Linux高性能服务器编程——学习笔记①
- Jmeter的性能测试