C4.5决策树的基本建模流程

C4.5决策树的基本建模流程

作为ID3算法的升级版，C4.5在三个方面对ID3进行了优化：

（1）它引入了信息值（information value）的概念来修正信息熵的计算结果，以抑制ID3更偏向于选择具有更多分类水平的列进行展开的情况，从而间接地抑制模型过拟合的倾向；
（2）C4.5新增了对连续变量的处理方法，采用类似于CART树的方法来寻找相邻取值的中间值作为切分点；
（3）C4.5加入了决策树的剪枝流程，以进一步提升模型的泛化能力。

然而，需要注意的是，尽管C4.5进行了这些改进，但它仍然只能解决分类问题，其本质仍然是一种分类树。

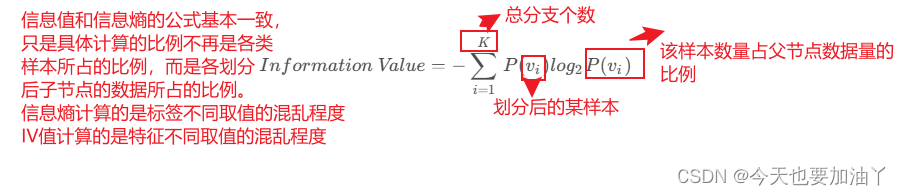
C4.5中信息值（以下简称IV值）是一个用于衡量数据集在划分时分支个数的指标，如果划分时分支越多，IV值就越高。具体IV值的计算公式如下：

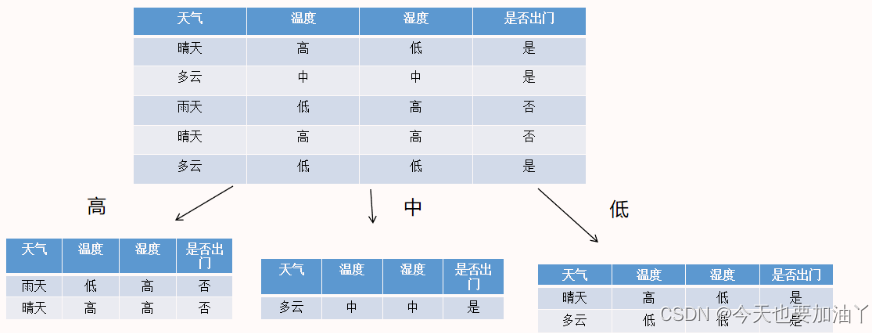
上次介绍的ID3决策树的建模流程中，

以湿度的不同取值为划分规则时：

IV = $?\frac{2}{5}?lo{g}_2\frac{2}{5}$-$\frac{1}{5}?lo{g}_2\frac{1}{5}$-$\frac{2}{5}?lo{g}_2\frac{2}{5}$=1.52

C4.5采用增益比例（Gain Ratio，被称为获利比例或增益率），来指导具体的划分规则的挑选。GR的计算公式如下：
$$GainRatio=\frac{InformationGain}{InformationValue}$$
上面的GR值为：$\frac{gain}{IV}$=$\frac{0.97}{1.52}$=0.64

然后据此进一步计算其他各列展开后的GR值，并选择GR较大者进行数据集划分

C4.5的连续变量处理方法:和CART树一致。即在连续变量中寻找相邻的取值的中间点作为备选切分点，通过计算切分后的GR值来挑选最终数据集划分方式。

在sklearn的树模型介绍文档中，有一段关于sklearn的决策树不支持离散变量建模的说明，其意为不支持按照类似ID3或C4.5的方式直接将离散变量按列来进行展开，而是根据sklearn中集成的CART树自身的建模规则，使得sklearn中的决策树实际上在处理特征时都是按照C4.5中连续变量的处理方式在进行处理，并非指的是带入离散变量就无法建模。