LeetCode 1954. 收集足够苹果的最小花园周长

一、题目

1、题目描述

给你一个用无限二维网格表示的花园，每一个?整数坐标处都有一棵苹果树。整数坐标?(i, j)?处的苹果树有?|i| + |j|?个苹果。

你将会买下正中心坐标是?(0, 0)?的一块?正方形土地?，且每条边都与两条坐标轴之一平行。

给你一个整数?neededApples?，请你返回土地的?最小周长?，使得?至少?有?neededApples?个苹果在土地?里面或者边缘上。

|x|?的值定义为：

• 如果?x >= 0?，那么值为?x
• 如果?x <?0?，那么值为?-x

2、接口描述

class Solution {
public:
    long long minimumPerimeter(long long neededApples) {
    }
};

3、原题链接

1954. 收集足够苹果的最小花园周长

---

二、解题报告

1、思路分析

每个位置是|i| + |j|个苹果，而且限制区域为以原点为中心的正方形，那么一定是有数学规律的。

其实可以分为四个数目相等的区域，为什么呢？

可以由|x| + |y| = k的函数图像得知，也可以观察发现

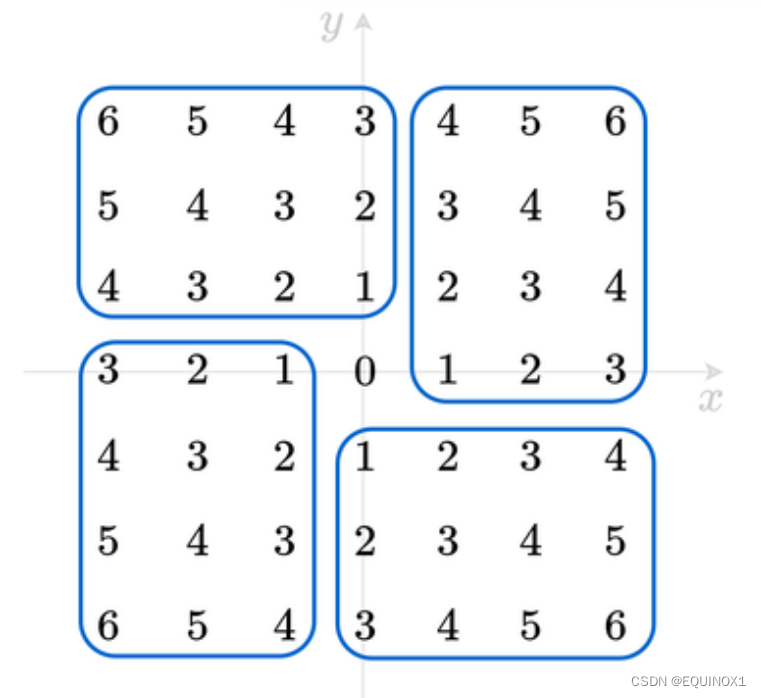
我们只需要计算出一个区域内的值然后乘4即可

我们设边长2n（由于以原点为中心，所以边长为偶数）

那么对于一个区域来说有n行n+1列

第一行为(n+1) * n / 2，每一行都比前一行多n，显然是首项为(n+1) * n / 2公差为n的等差数列

我们求得一个区域的总数然后乘4即可

sum = 4*n^3 + 6*n^2 + 2*n?

2、复杂度

由于log(1000000)大概也就20上下，所以时间复杂度为O(1)

时间复杂度： O(1) 空间复杂度：O(1)

3、代码详解

?

class Solution {
public:
    long long minimumPerimeter(long long neededApples) {
        long long l = 1  , r = 1000000 , s = 0 , mid = 0;
        while(l < r)
        {
            mid = (l + r) >> 1;
            s = (4*mid*mid*mid + 6*mid*mid + 2*mid);
            if(s >= neededApples) r = mid;
            else l = mid + 1;
        }
        return r << 3;
    }
};