各种进制之间的转换是怎么进行的（二，八，十，十六）超级详细

目录

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

---

目录

? ? ? ? ? ? ?进制的介绍：

二进制和其他进制之间的转换：

二进制转八进制：

二进制转十进制：

二进制转十六进制：

八进制和其他进制间的转换：

八进制转二进制：

八进制转十进制：

八进制转十六进制：

十进制转和各个进制的转换

十进制转二进制：

十进制转八进制：

十进制转十六进制：

十六进制转和各个进制的转换

十六进制转二进制：

十六进制转八进制：

十六进制转十进制：

---

进制的介绍：

我们使用的数字，其实就是十进制的数字，十进制是由0~9组成，共10个数字，因为要逢十进一所以叫做十进制。

二进制是由0和1组成，共2个数字，要逢二进一

八进制由0~7组成，共8个数字，要逢八进一

十六进制由0~9 和a b c d e f 组成，共16个数字，其中a表示10，b表示11，c表示12，d表示13，e表示14，f表示15，要逢十六进一

而二，八，十六进制是计算机里采用的数字，它们之间又有什么关系呢？和我们生活中的十进制又有怎样的联系呢？下面一一道来

---

二进制和其他进制之间的转换：

二进制转八进制：

例如二进制数：100100

三位二进制数对应一位八进制数

采用421原则：每位的权分别为：22，21，2?,也就是 4,2,1

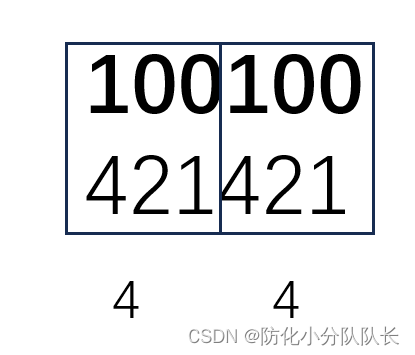
二进制数100100转换成八进制数是44

再举一个例子：

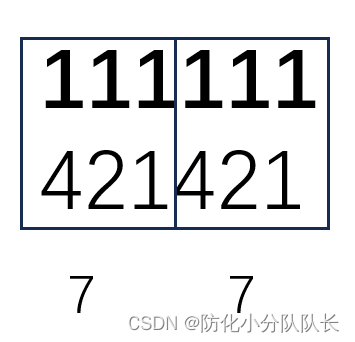
二进制数111111转换成八进制数是77

421原则：从右向左三位二进制数对应一位八进制数，看421上面对应是是0还是1，是1采用下面的数，是0则不采用，如果有多个1，则下面对应的数相加

---

二进制转十进制：

例如二进制数：100100

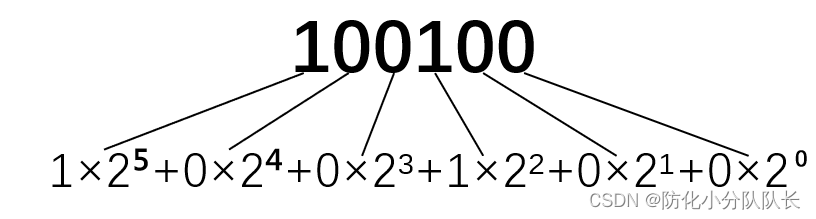
从右向左依次用2?乘展开的数然后相加：32+0+0+4+0+0=36

所以二进制的100100转换成十进制就是36

再举一个例子：

例如二进制数：111111

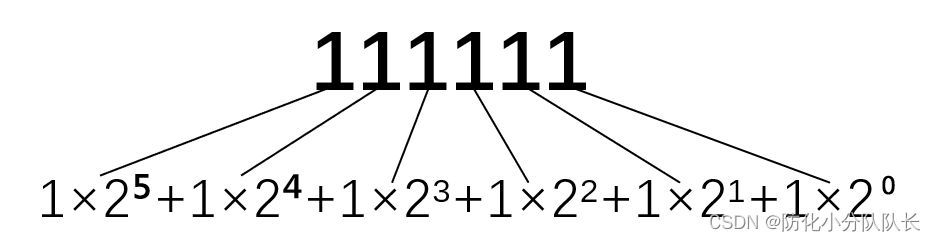
从右向左依次用2?乘展开的数然后相加：32+16+8+4+2+1=63

（任何数的0次方都是1）

所以二进制的111111转换成十进制就是63

---

二进制转十六进制：

例如二进制数111100：

四位二进制数对应一位十六进制数

采用8421原则：每位的权分别为：23，22，21，2?,也就是 8,4,2,1

二进制数111100转换成十六进制数是3c（十六进制中c代表12）

例如二进制数100100：

二进制数100100转换成十六进制数是24

用8421原则：从右向左四位二进制数对应一位十六进制数，看8421上面对应是是0还是1，是1采用下面的数，是0则不采用，如果有多个1，则下面对应的数相加

此时，二进制转换八进制，十进制，十六进制就已经一一介绍了

---

八进制和其他进制间的转换：

八进制转二进制：

一位八进制数对应三位二进制数

依然采用421原则：

例如八进制数77：

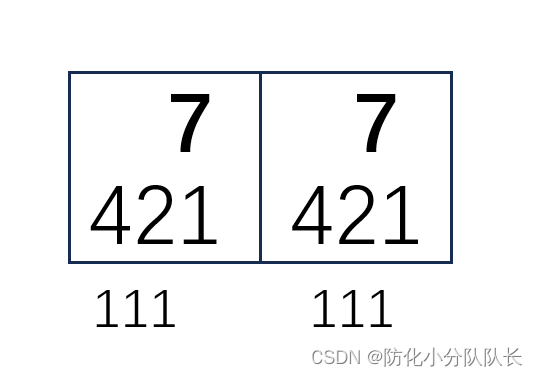
421原则：八进制转二进制，八进制数77每位对应三位二进制数，所以结果是六位二进制数，421看那几个数能组成7，如果相加正好7，在421的下面就是1，所以八进制数77转换成二进制数是111111

例如八进制数44：

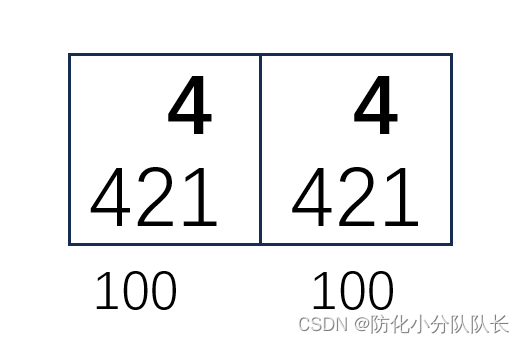
421原则：八进制转二进制，八进制数44每位对应三位二进制数，所以结果是六位二进制数，421看那几个数能组成7，如果相加正好7，在421的下面就是1，如果没有就是0，所以八进制数44转换成二进制数是100100

---

八进制转十进制：

八进制数77：和二进制转十进制类似

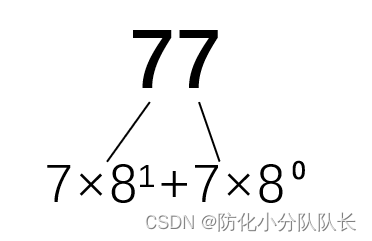
从右向左依次用8?乘展开的数然后相加：7×81+7×8?=63

例如八进制数44：

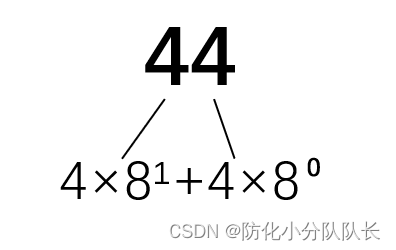
从右向左依次用8?乘展开的数然后相加：4×81+4×8?=36

---

八进制转十六进制：

八进制无法直接转到十六进制 需要八进制转换成二进制 再用二进制转换成十六进制

上文已经讲到八进制转二进制以及二进制转十六进制，此处不再一一展开

---

十进制转和各个进制的转换

十进制转二进制：

例十进制数36

利用除2取余法（小于2也要在除一次，直到最后为0不在进行）

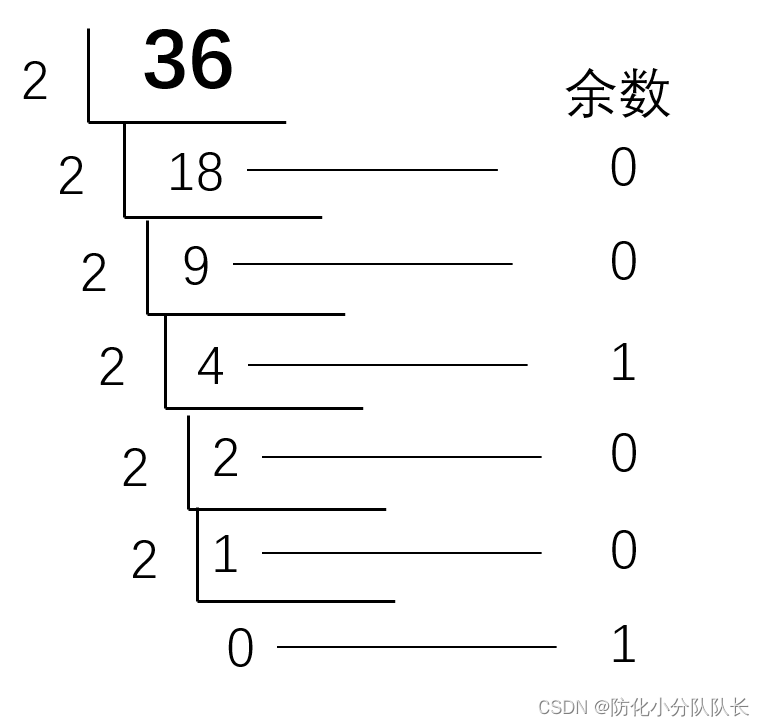
除2取余法：从下往上，十进制36转换成二进制是100100

例2：十进制数63转二进制

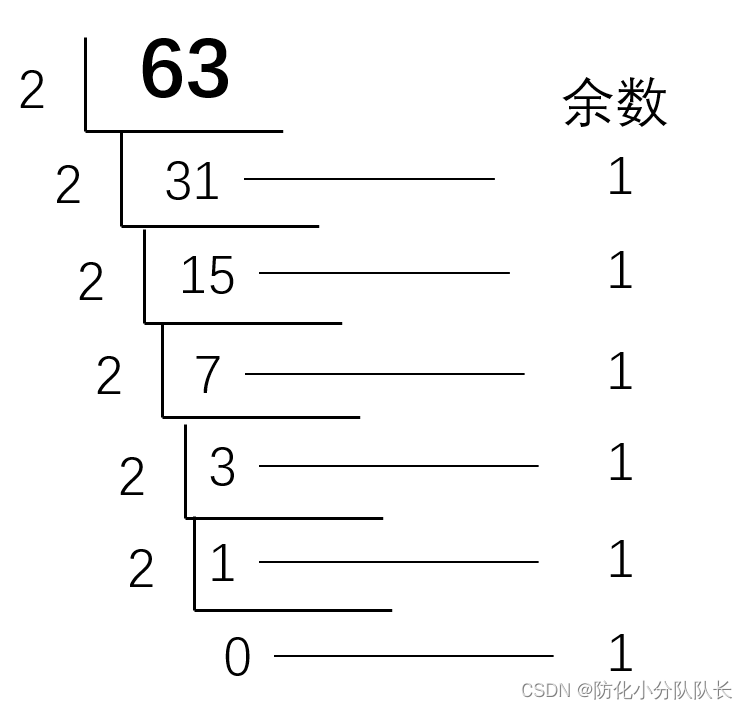
除2取余法：从下往上，十进制63转换成二进制是111111

---

十进制转八进制：

例1十进制数36：

利用除8取余法（小于8也要在除一次，直到最后为0不在进行）

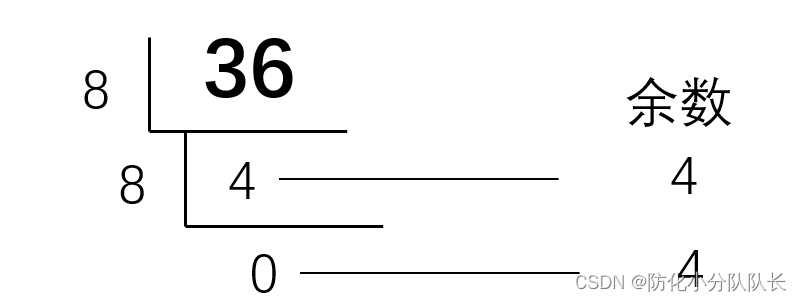
除8取余法：从下往上，十进制36转换成八进制是44

例2十进制数63：

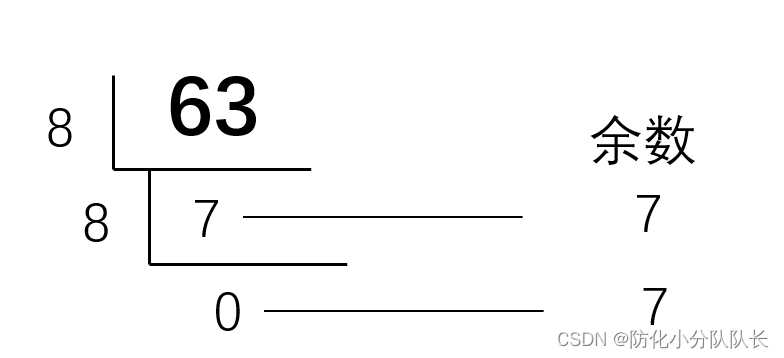
除8取余法：从下往上，十进制63转换成八进制是77

---

十进制转十六进制：

例1十进制数36：

利用除16取余法（小于16也要在除一次，直到最后为0不在进行）

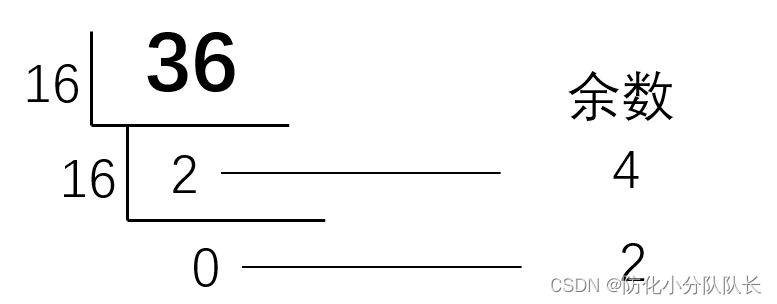
除16取余法：从下往上，十进制数36转换成十六进制数是24

例2十进制数63：

除16取余法：从下往上，十进制数63转换成十六进制数是3f（十六进制15用f表示）

---

十六进制转和各个进制的转换

十六进制转二进制：

8421原则

例1十六进制数3c

8421原则：十六进制转二进制，十六进制数3c（c在十六进制中表示12）每位对应四位二进制数，所以结果是八位二进制数，8421看那几个数能组成3，如果相加正好3，则对应的数字下面是1否则是0，8421看那几个数能组成12，如果相加正好12，则对应的数字下面是1否则是0，所以十六进制数3c转换成二进制数是00111100

例2十六进制数11

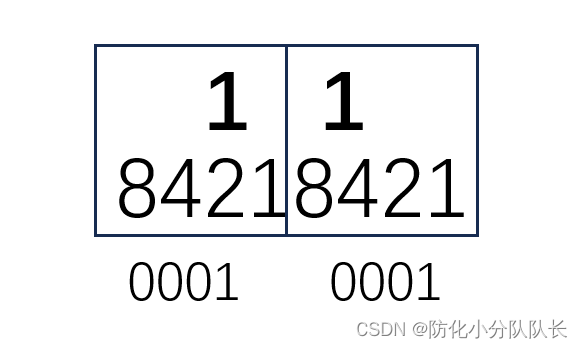
8421原则：十六进制转二进制，十六进制数11每位对应四位二进制数，所以结果是八位二进制数，8421看那几个数能组成1，则对应的数字下面是1否则是0，所以十六进制数11转换成二进制数是00010001

---

十六进制转八进制：

十六进制也无法直接转成八进制，只能通过十六进制转二进制在转成八进制。

---

十六进制转十进制：

例1十六进制数3c

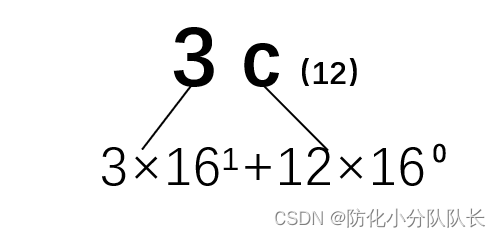
从右向左依次用16?乘展开的数然后相加：48+12=60

所以十六进制的3c转换成十进制就是60

例2十六进制数11

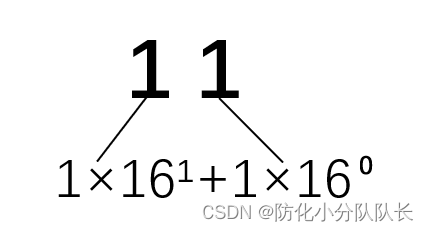
从右向左依次用16?乘展开的数然后相加：16+1=17

所以十六进制的11转换成十进制就是17

---

---

注意注意注意：n?=1！！！！！