N-皇后问题（DFS）

?

?DFS步骤

（1）先判断递归是否到达终点（递归深度 u == n 时到达终点），是的话说明当前路径是能满足题意、走到最后的正确路径，此时输出结果；

（2）若未到达终点，则递归调用 dfs 函数。调用前判断当前点是否已经访问，未访问则标记为访问，防止重复进入该点；调用后标记当前点为未访问，方便回溯。

难点

（1）以3-皇后问题为例，为了找出所有可能性，应该用一个 for 循环对第一行的 3 列进行遍历，同时在 for 循环里再写一个 for 循环遍历第二行的 3 列，再在里面写一个 for 遍历第三行的 3 列，即 n 为几就需要几层 for 循环嵌套，因此使用递归模拟 for 循环嵌套。

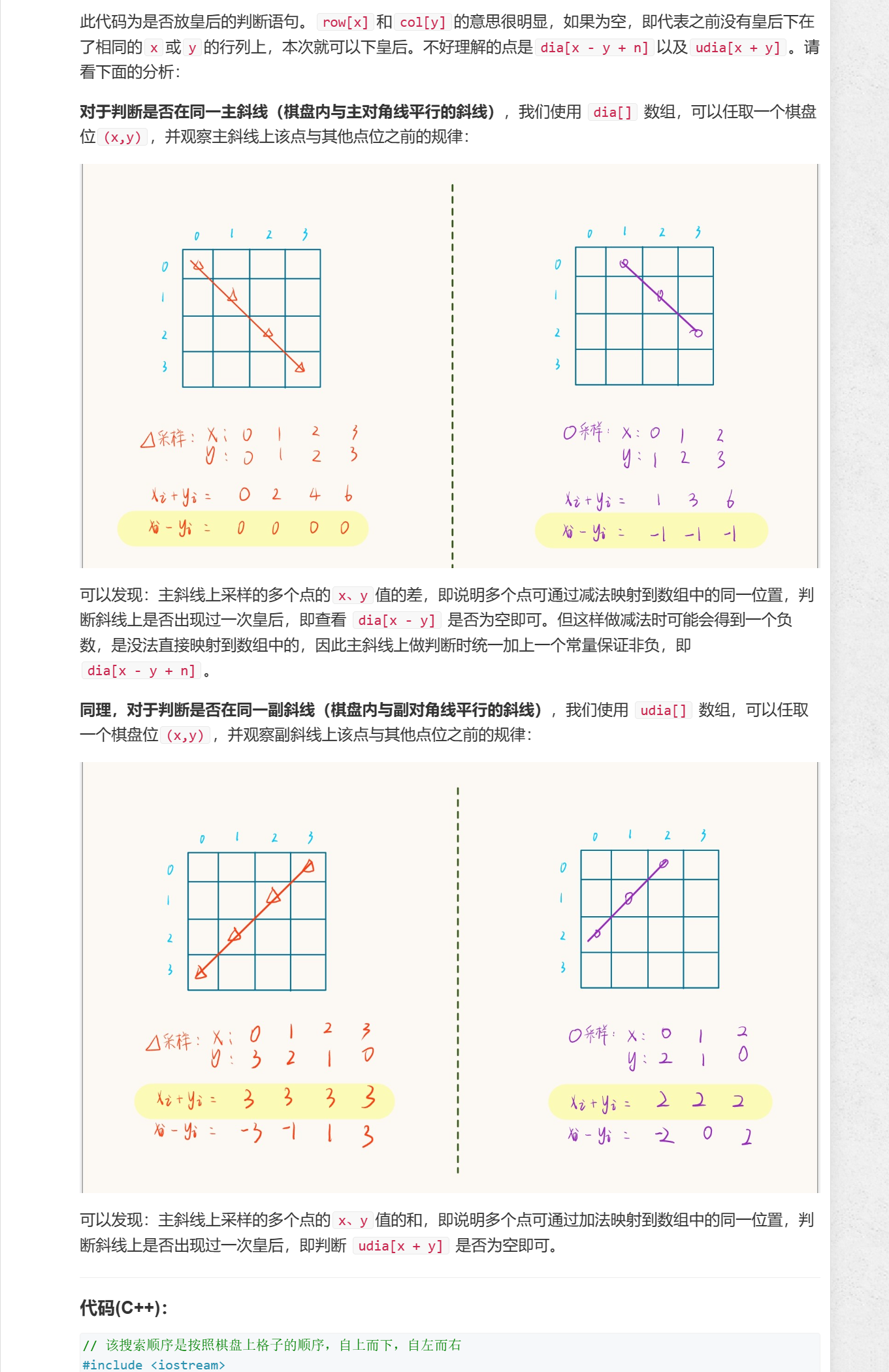
（2）另一个难点是：如何判断正副对角线是否访问过，在这里引用AcWing 843. n-皇后问题 —— 主副斜线的“秘密” - AcWing里的解析，并且提供一种便捷的记忆法

主对角线，即 y = -x + b，则截距 b = y + x，代码中用 i 表示 x，用 u 表示 y，故 dg[ u + i ]

副对角线，即 y = x + b， 则截距 b = y - x ，但是 y - x 有可能出现负数，这样会造成数组越界，不过只需加上任意常数保证其值大于等于 0（如n）即可，故某个点对应的副对角线为 udg[ u - i + n?]

#include<iostream>
using namespace std;

int n;
int g[15][15];
bool col[15], dg[20], udg[20];
// dg表示主对角线，udg表示副对角线

void dfs(int u) // 遍历的是第u行
{
    if(u == n) // 递归到达终点，则输出结果
    {
        for(int i=0;i<n;++i)
        {    
            for(int j=0;j<n;++j)
            {
                printf("%c", g[i][j]);
            }
            printf("%c", '\n');
        }
        printf("%c", '\n');
        return;
    }
    
    for(int i=0;i<n;++i)//遍历的是一行里的不同列
    {
        if(!col[i] && !udg[u-i+n] && !dg[i+u])
        {
            g[u][i] = 'Q';
            col[i] = udg[u-i+n] = dg[i+u] = true;
            dfs(u+1); // 遍历下一行，也就是利用递归实现了for循环的嵌套
            col[i] = udg[u-i+n] = dg[i+u] = false;
            g[u][i] = '.';
        }
    }
}

int main()
{
    scanf("%d", &n);
    
    for(int i=0;i<n;++i)
        for(int j=0;j<n;++j)
            g[i][j] = '.';
            
    dfs(0);
    
    return 0;
}