Peter算法小课堂—浮点数危机

大家先想想下面这个代码运行结果：

#include <bits/stdc++.h>
using namespace std;
int main(){
	double x=5.2;
	double y=4.1+1.1;
	cout<<(x<y)<<endl;
	cout<<x-y<<endl;
	return 0;
}

最终发现，

？？？但凡一个学过数学的人都知道4.1+1.1=5.2，难道……计算机CPU爆掉了？

其实，计算机在用二进制储存浮点数时会有误差，比如我们要凑0.2，计算机会先凑0.125，再凑0.0625，再再……，最终还是有那么一丢丢的误差。那么，我们就不能比较大小了吗？

再看一个代码：

#include <bits/stdc++.h>
using namespace std;
const double ERR=0.00000001;
int main(){
	double x=5.2;
	double y=4.1+1.1;
	cout<<(fabs(x-y)<ERR)<<endl;//判断浮点数"=="
	cout<<(x>y+ERR)<<endl;//判断浮点数">"
	cout<<(x<y-ERR)<<endl;//判断浮点数"<"
	cout<<(x>y-ERR)<<endl;//判断浮点数">="
	return 0;
}

结果……

不出所料，这一次竟然答对了！Emm……怎么理解呢

相信前3个大家一定理解，前面讲过是精度捣的乱。那最后一个呢？

我们用数轴来解释，

数轴： y-ERR? ? ? ? ? ?y? ? ? ? ? ? ? ?y+ERR

那么，我们但凡x在[y-ERR,y+ERR]里面，都算x=y，因为误差嘛。那x>=y就相当于x>y||x==y，即y-ERR<x

让我们大展身手八

计算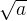，保留两位小数

那么，一般人都用sqrt，我们呢……我们是高（蒟）手（蒻），必须用二分

分析：二分，枚举答案，很简单

代码：

#include <bits/stdc++.h>
#define ERR 0.000001
using namespace std;
typedef double d;
d a;
bool tooSmall(d x){return x*x<=a;}
int main(){
	cin>>a;
	d l=0;
	d r=1000;
	d ans=1;
	while(r-l>ERR){
		d mid=l+(r-l)/2;
		if(tooSmall(mid)) ans=l=mid;
		else r=mid;
	}
	cout<<fixed<<setprecision(2)<<ans<<endl;
	return 0;
}

?太戈编程427题

题目描述：

对于一元三次方程： x^3+x^2+x=a， 它的形式很特殊，我们可以证明它的解只有一个。

分析：和前一题差不多

代码：

#include <iostream>
#include <cmath>
#include <iomanip>
using namespace std;
const double ERR=0.000001;
double a;
bool tooSmall(double x){
	return pow(x,3)+pow(x,2)+x<a;
}
int main(){
	cin>>a;
	double l=-100,r=100;
	while(r-l>ERR){
		double mid=l+(r-l)/2;
		if(tooSmall(mid)) l=mid;
		else r=mid;
	}
	cout<<fixed<<setprecision(3)<<r<<endl;
	return 0;
}

当然，我有个朋友，他是个蒟蒻，他只学到for循环，也做了这道题，AC了，给大家看看代码，嘲笑一下

#include <bits/stdc++.h>
using namespace std;
int main(){
	double a,ans,Min=1000;
	cin>>a;
	for(double x=-10;x<=10;x+=0.001){
		double d=fabs(x*x*x+x*x+x-a);
		if(d<Min) Min=d,ans=x;
	}
	cout<<fixed<<setprecision(3)<<ans<<endl;
	return 0;
}

这也可以，好吧……

送礼就要体面

这道题洛谷里没有，我截图

请大家简要概括本题，语文？

其实这题就是相当于0/1分数规划

来推导吧！

这题还是用二分

二分

是否存在礼品集合S，含k个礼品，使得：k个礼品的性价比大于等于x

相当于，奇妙的数学

下面进行推导

#include <bits/stdc++.h>
using namespace std;
const int N=100000;
const int ERR=0.000001;
int n,k,p[N],v[N],z[N];
bool OK(double x){
	for(int i=0;i<n;i++) z[i]=v[i]-x*p[i];
	sort(z,z+n);
	double sum=0;
	for(int i=n-k;i<n;i++) sum+=z[i];
	return sum>=0;
}
int main(){
	cin>>n>>k;
	for(int i=0;i<n;i++) cin>>v[i]>>p[i];
	double maxv=*max_element(v,v+n);
	double minp=*min_element(p,p+n);
	double l=0,r=maxv/minp,ans=0;
	while(r-l>ERR){
		double mid=l+(r-l)/2;
		if(OK(mid)) ans=l=mid;
		else r=mid;
	}
	cout<<ans<<endl;
	return 0;
}

希望这些对大家有用，三连必回