Transformer - 注意力机制
文章目录
1. Self-attention
自注意力机制。
解决的问题:到目前为止,我们的Input都是一个向量,输出是一个数值或者一个类别。如果我们的输入是一排向量,且输入的向量的输入数目会改变,那么该怎么处理?
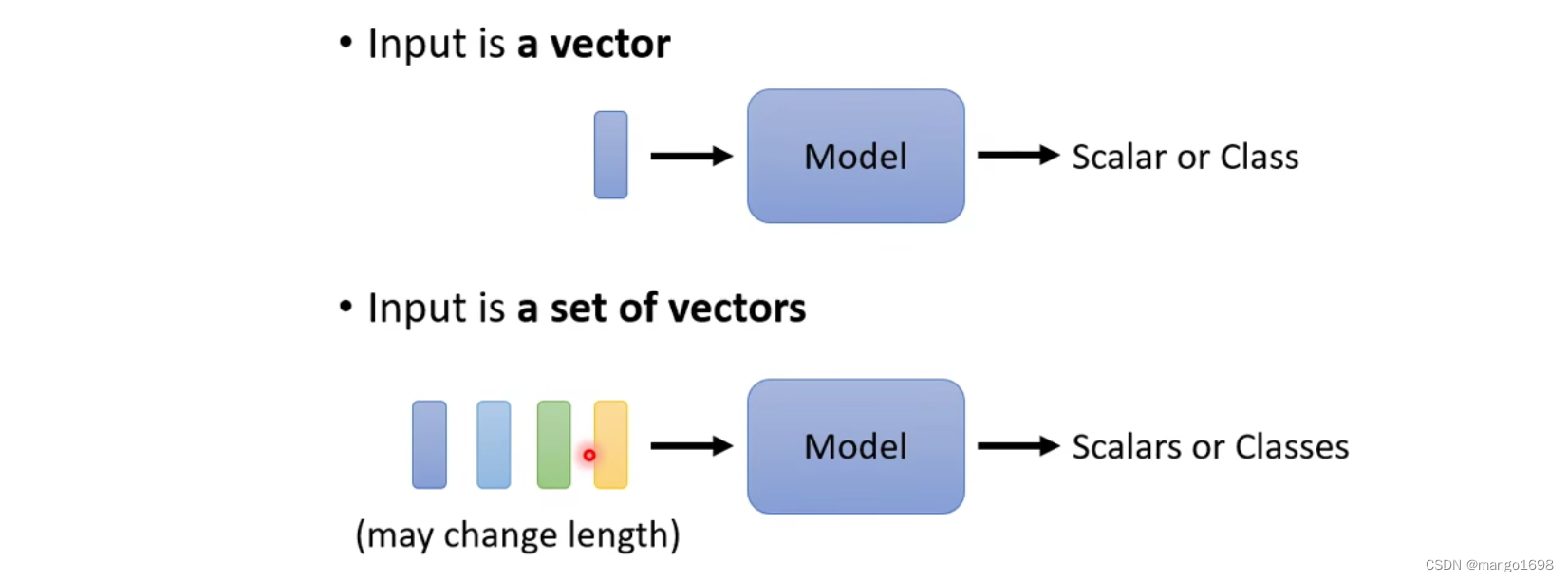
如,我们输入一个句子,句子长短不一样,那么输入的向量数目就会不一样。
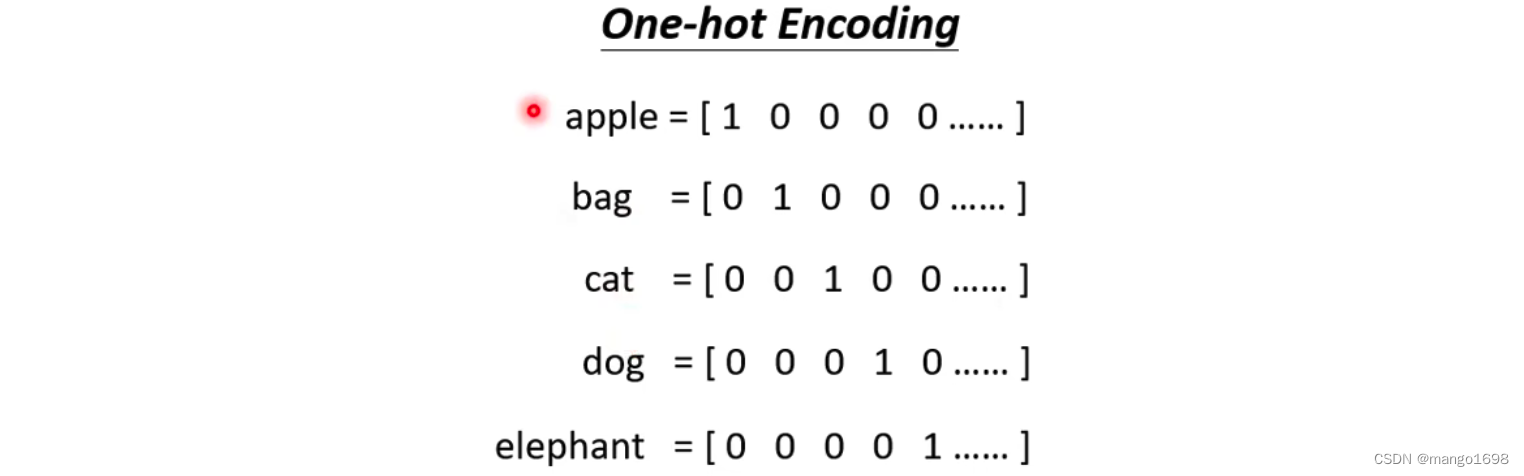
将一个词汇表示成一个向量
- 使用one-hot encoding方法
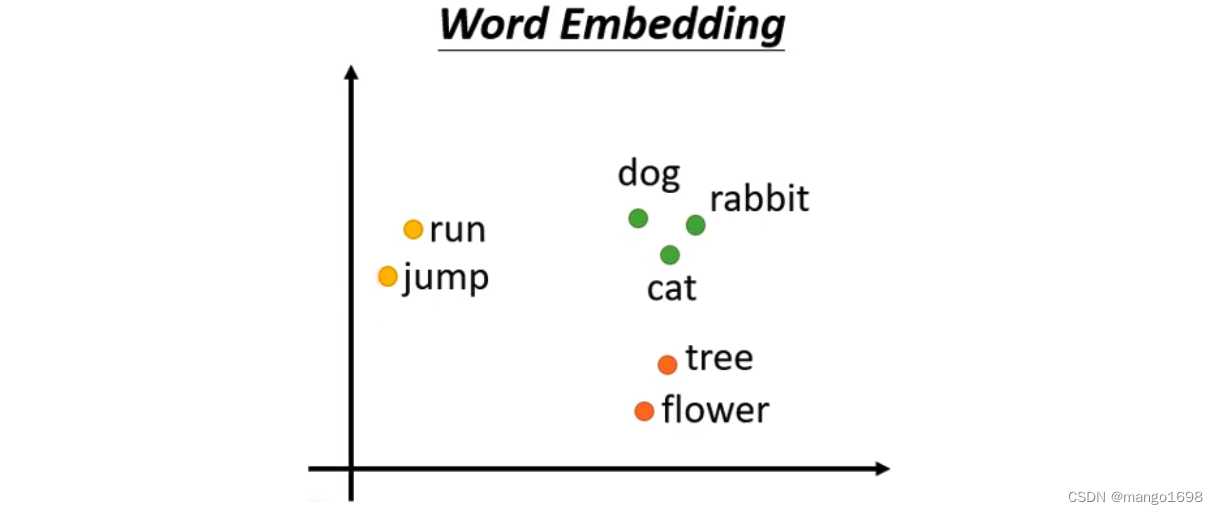
- 使用word embedding方法
声音、图等等都是可以表示成一堆向量。
输出类型:
- 每个向量都有一个对应的label(Sequence Labeling)

- 整体只需要输出一个label

- 不知道该输出多少个label,机器自己决定应该输出多少个label,这种任务叫做seq2seq。

如:翻译,语音转文字等。
现在,只考虑每个向量都有一个对应的label
像词性分类,如下
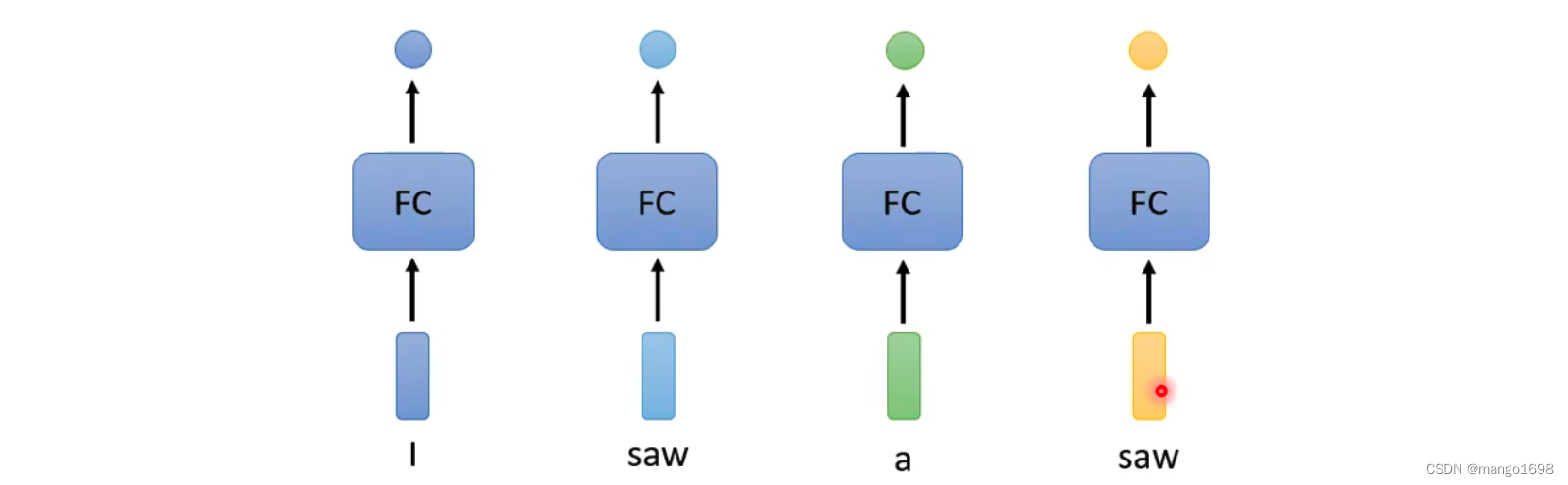
这样,显然存在很大的问题,对于saw在这里面既是名词,又是动词。所以,我们就想让全连接层考虑更多的上下文信息。
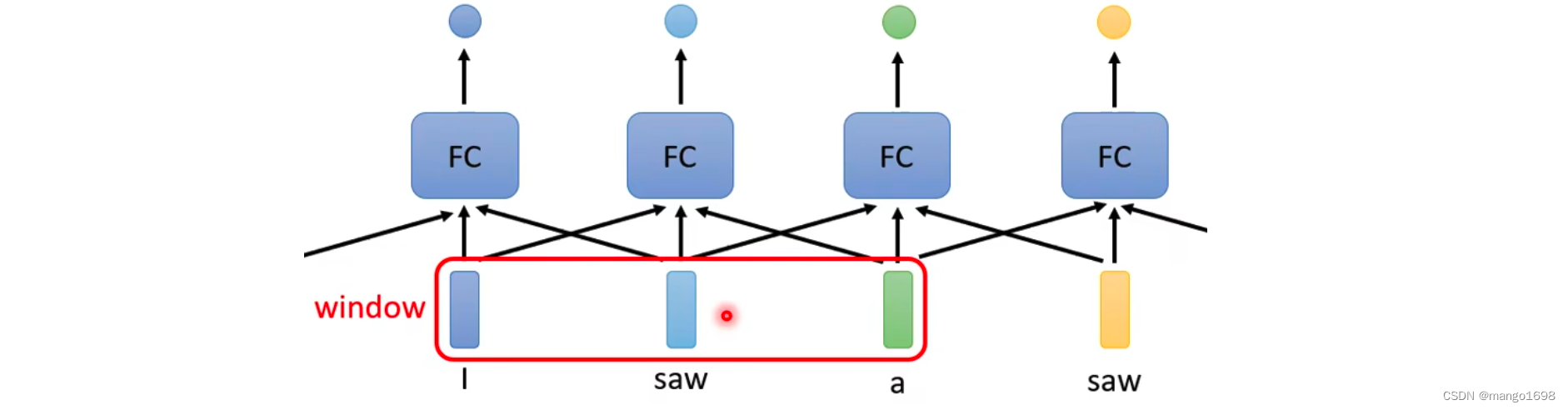
但是,如上这种方法还是存在问题的。如果我们有某一个任务,不是要考虑一个window就可以解决的,而是要考虑一整个序列信息才能解决,那么该怎么解决呢?如果简单的将window扩大,但是这样会存在问题,全连接层的参数量会非常大。
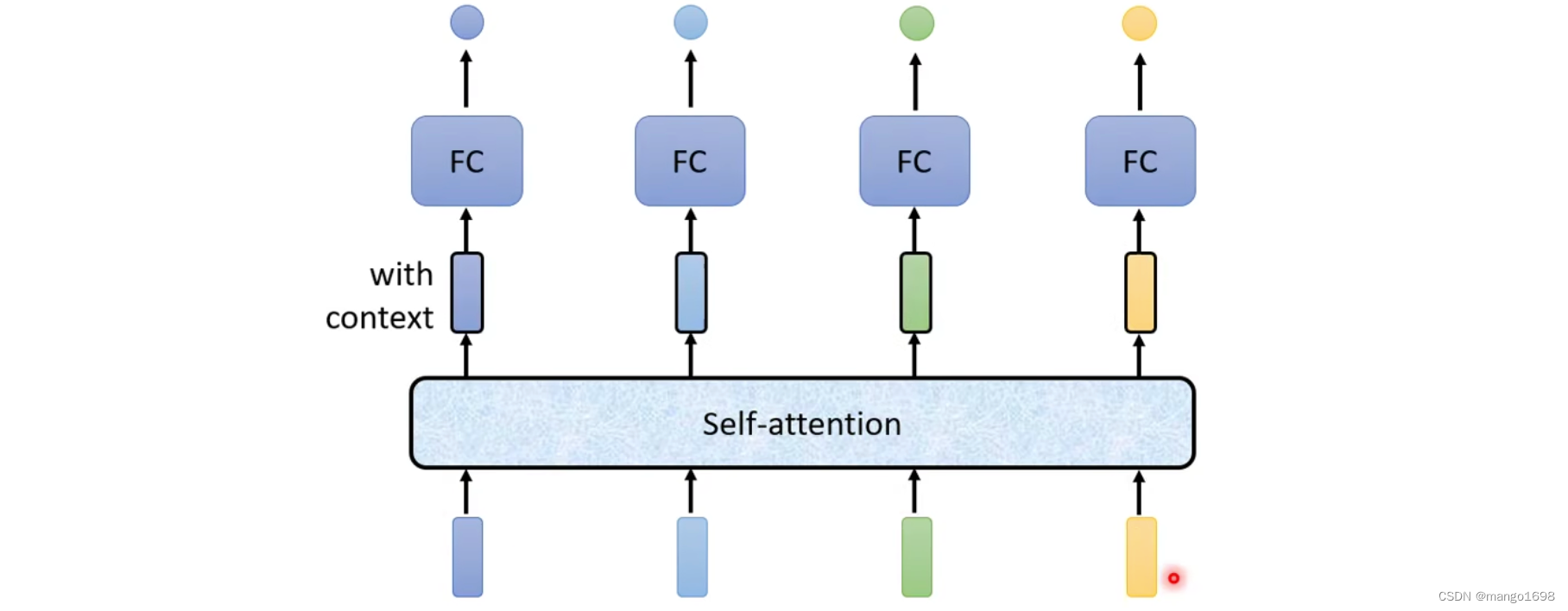
解决方法:Self-Attention
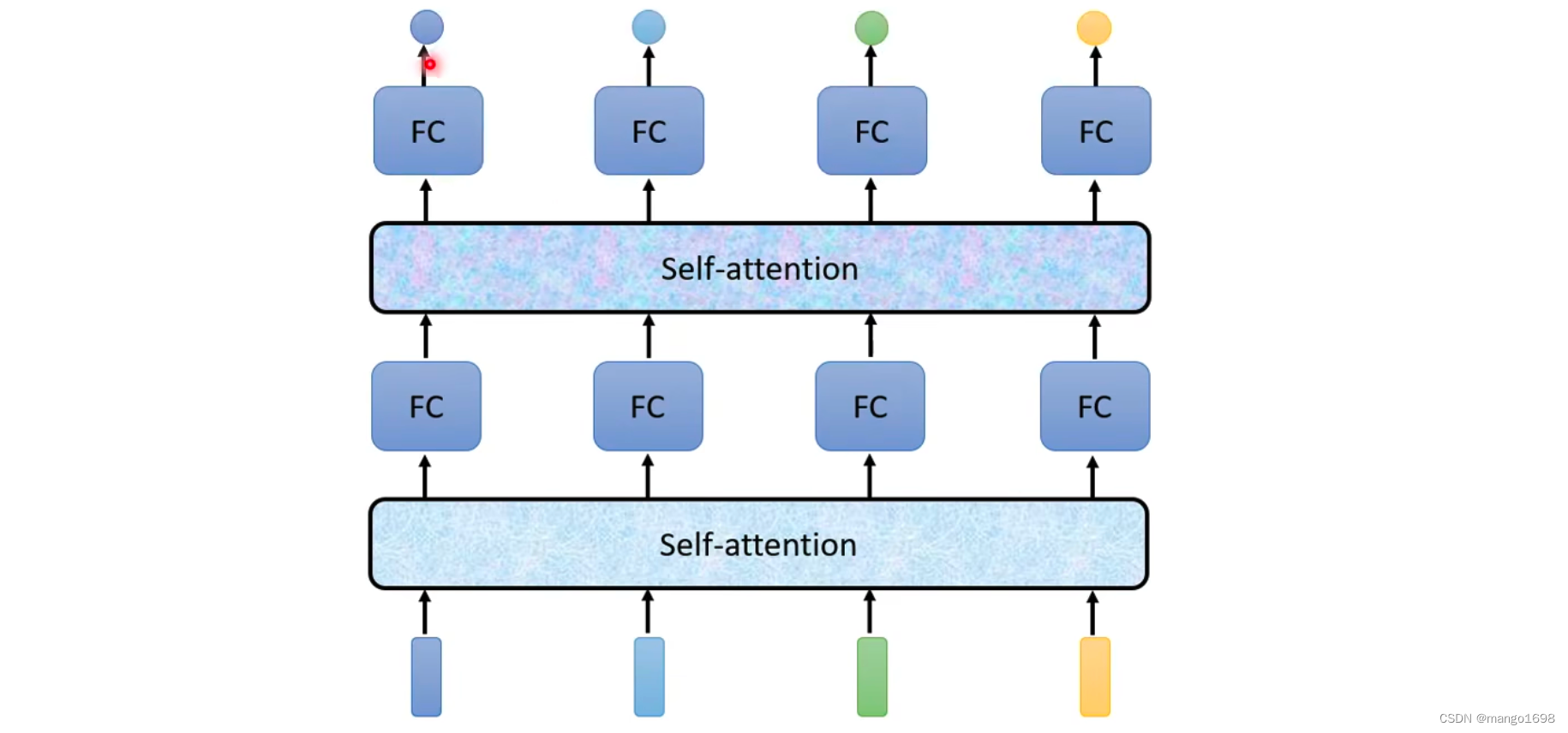
Self-attention可以叠加很多次。
Self-attention原理
输入为一串的向量,它可能整个网络的输入,也可能是某个隐藏层的输出。

那么,对于具体每个输出向量是怎么产生的呢?
对于 b 1 b^1 b1向量怎么产生,首先根据 a 1 a^1 a1找出输入序列里面跟 a 1 a^1 a1相关的其他向量。其他向量和 a 1 a^1 a1关联的程度用数值 α \alpha α进行表示。
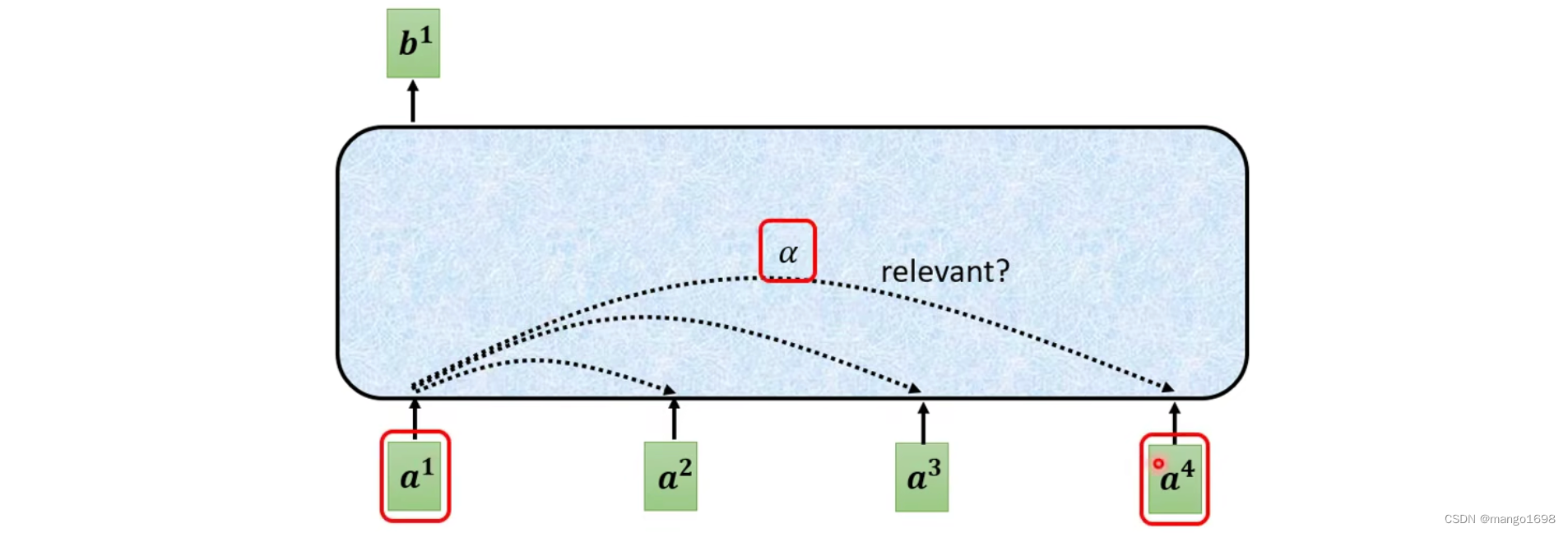
那么,self-attention怎么自动决定两个向量的关联性呢?
需要一个计算attention的模组,输入两个向量,输出两个向量的关联性 α \alpha α。
那么,对于 α \alpha α的值具体怎么计算呢?
有很多不同的办法,如Dot-product,Additive等。
-
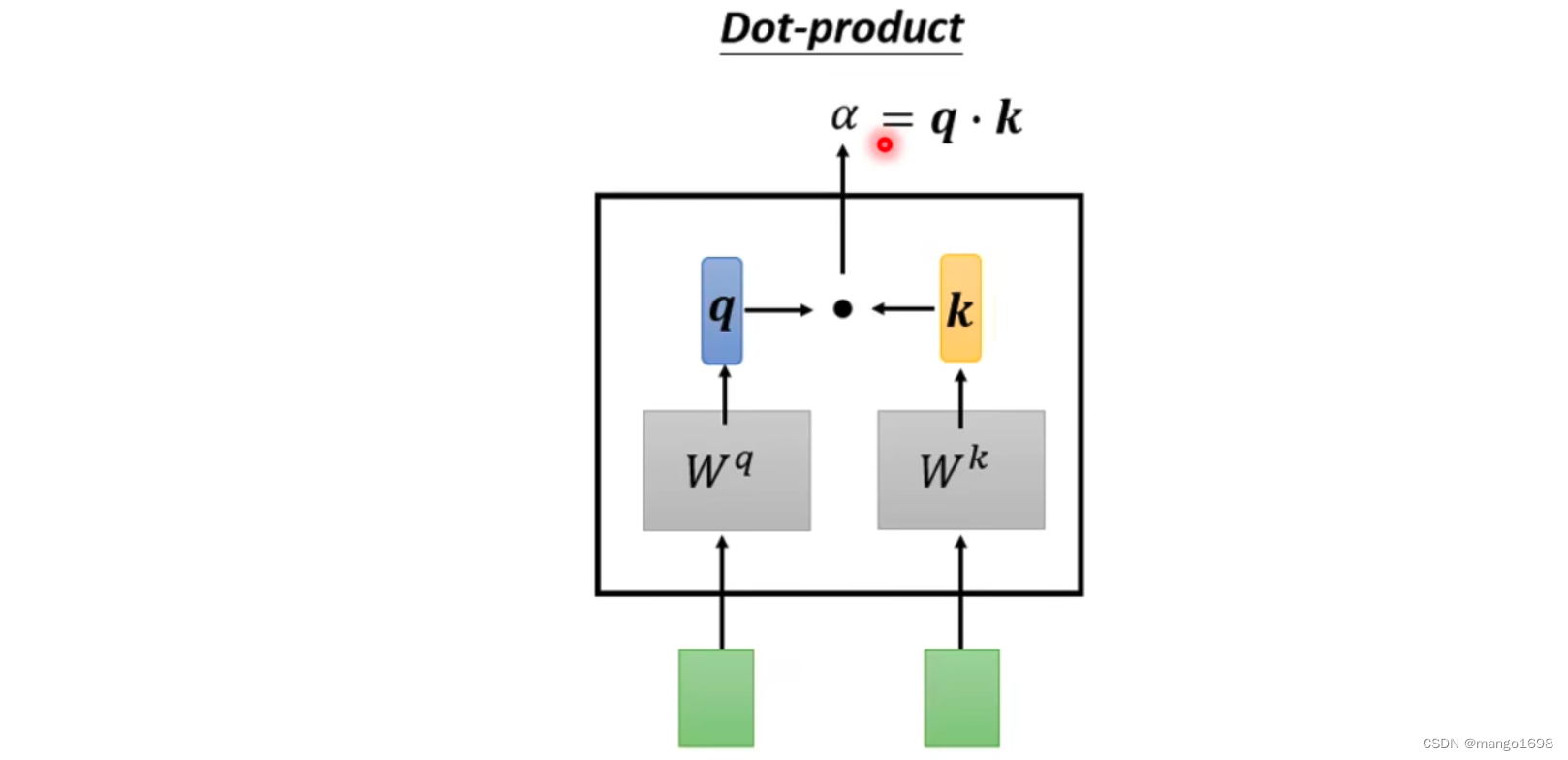
Dot-product
将两个输入向量,分别乘上两个不同的矩阵,然后得到 q , k q,k q,k两个向量,然后将 q , k q,k q,k做点积,结果就是 α \alpha α。
- Additive
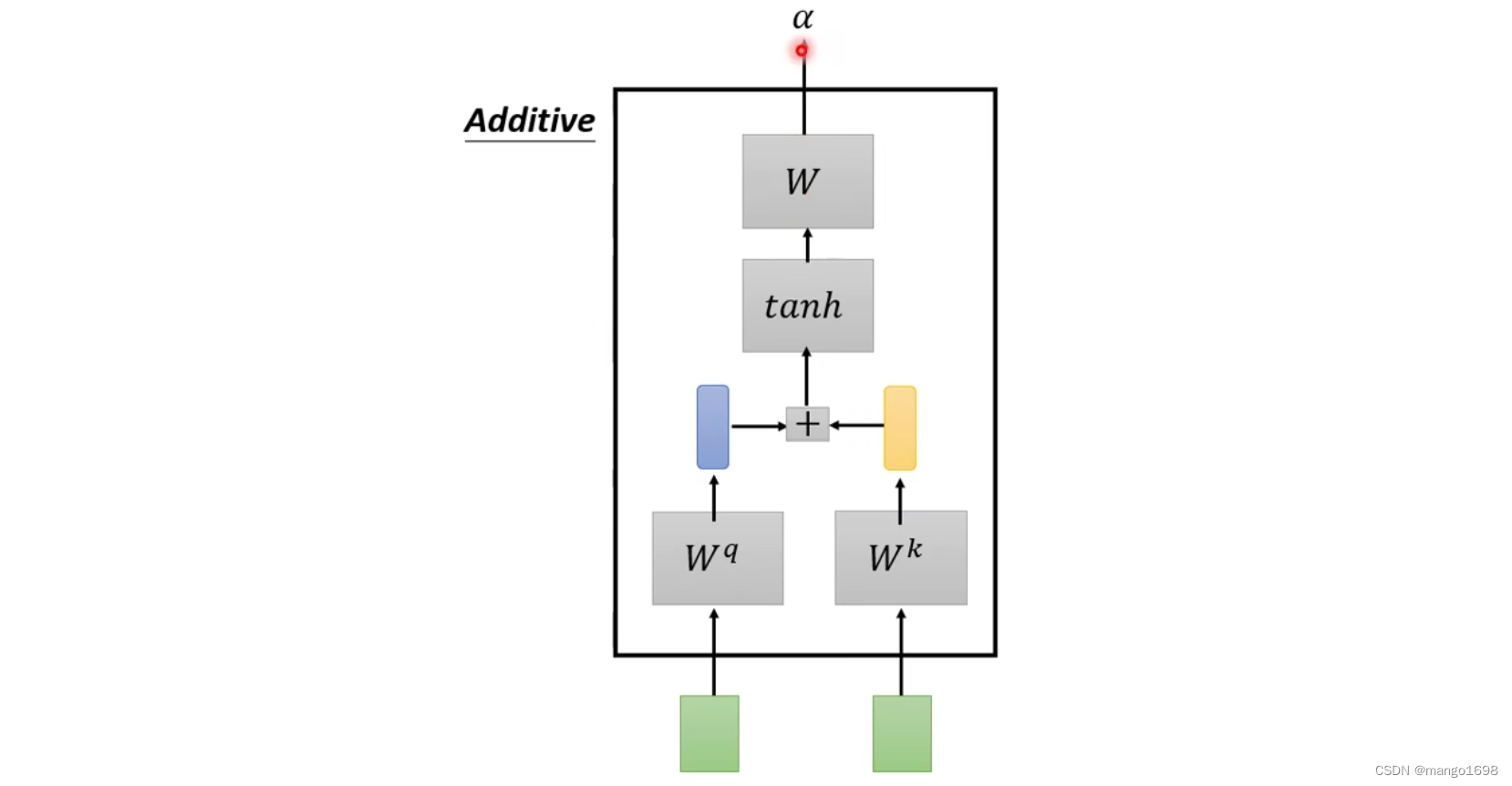
总之,有很多不同的方法来计算
α
\alpha
α。最常用的方法,也是用在Transformer中的方法就是Dot-product。
将该方法运用在Self-attention中:
q:query
k:key
将 a 1 a^1 a1分别与其他向量进行计算关联性 α \alpha α。将 a 1 a^1 a1乘以 W q W^q Wq得到 q 1 q^1 q1,其他向量 a 2 , a 3 , a 4 a^2,a^3,a^4 a2,a3,a4分别乘以 W k W^k Wk得到 k 2 , k 3 , k 4 k^2,k^3,k^4 k2,k3,k4。
如, q 1 = W q a 1 q^1 = W^qa^1 q1=Wqa1, k 2 = W k a 2 k^2=W^ka^2 k2=Wka2。那么, α 1 , 2 = q 1 ? k 2 \alpha_{1,2}=q^1·k^2 α1,2?=q1?k2。
这个
α
\alpha
α关联性也被称作attention score。
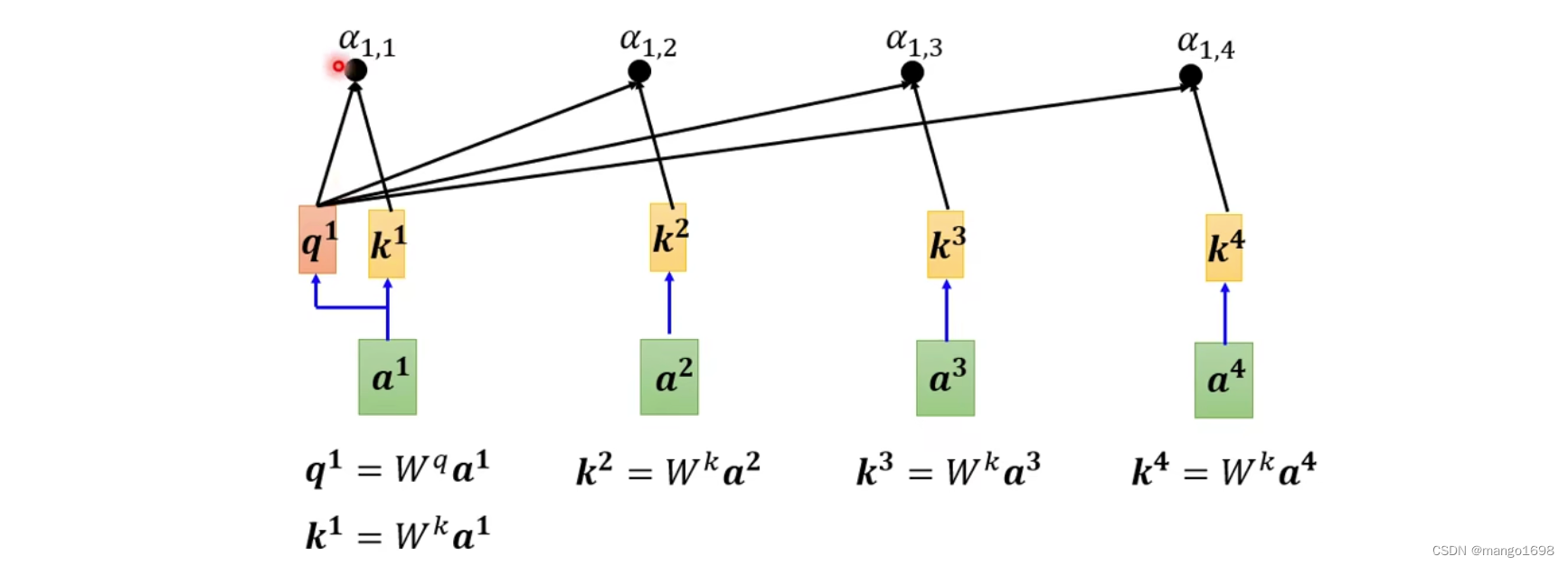
一般在实际操作的时候, a 1 a^1 a1也会和自己算关联性,得到 k 1 = W k a 1 k^1 = W^ka^1 k1=Wka1。
计算出 a 1 a^1 a1和其他每个向量的关联性后,后面会跟上一个softmax激活函数。这里不一定要用softmax,或者可以尝试使用ReLU或者其他。
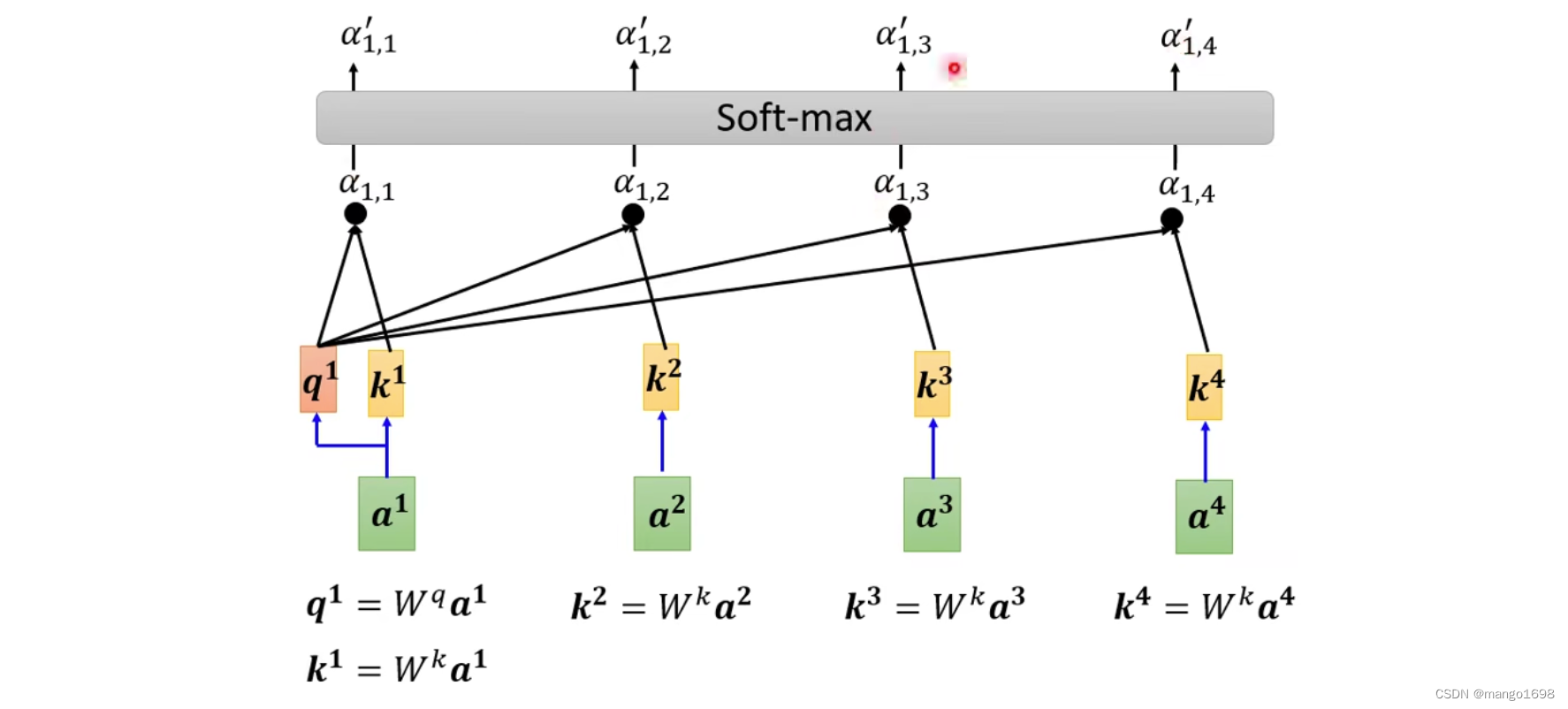
得到 α ′ \alpha' α′后,我们就要根据关联性 α ′ \alpha' α′抽取出这个序列中重要的信息。
那么,怎么抽取重要的信息呢?
将 a 1 , a 2 , a 3 , a 4 a^1,a^2,a^3,a^4 a1,a2,a3,a4每个向量乘上 W v W^v Wv得到新的向量 v 1 , v 2 , v 3 , v 4 v^1,v^2,v^3,v^4 v1,v2,v3,v4。然后,将 v 1 , v 2 , v 3 , v 4 v^1,v^2,v^3,v^4 v1,v2,v3,v4每个向量分别乘上对应的 α ′ \alpha' α′,最后将结果进行相加。

从矩阵计算角度进行分析: q i = W q a i q^i=W^qa^i qi=Wqai
可以将这些 a a a合起来,组成一个矩阵,如
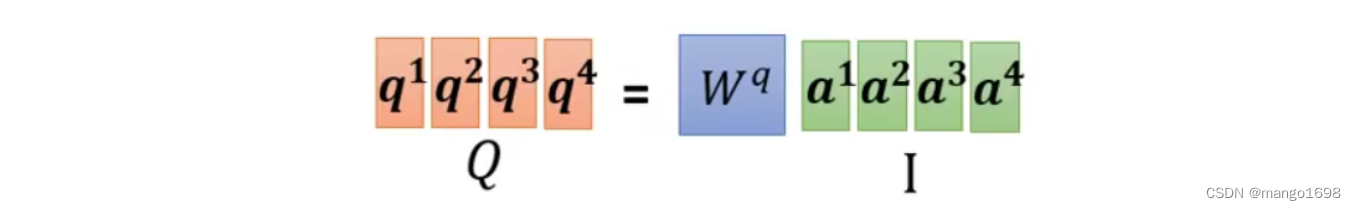
我们将 a a a组成的矩阵用 I I I进行表示,将结果 q q q组成的矩阵用 Q Q Q进行表示。所以,即 Q = W q I Q=W^qI Q=WqI
同理, k i = W k a i k^i=W^ka^i ki=Wkai,即 K = W k I K=W^kI K=WkI
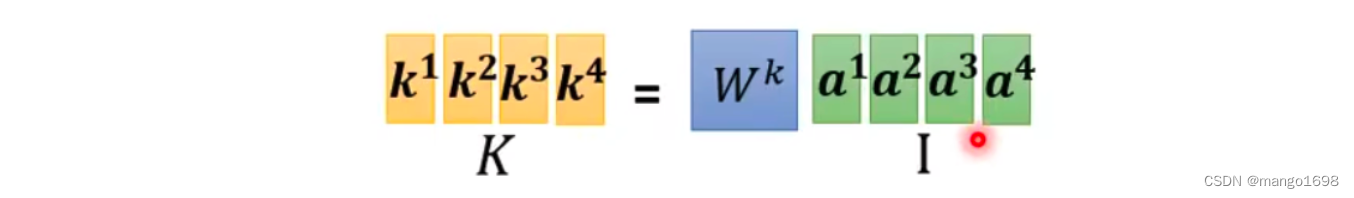
v i = W v a i v^i=W^va^i vi=Wvai,即 V = W v I V=W^vI V=WvI
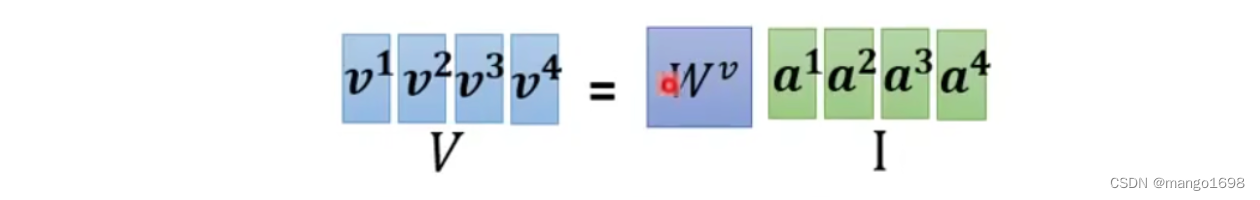
对于,求 α \alpha α的过程,我们也可以看作是矩阵与向量相乘的过程:
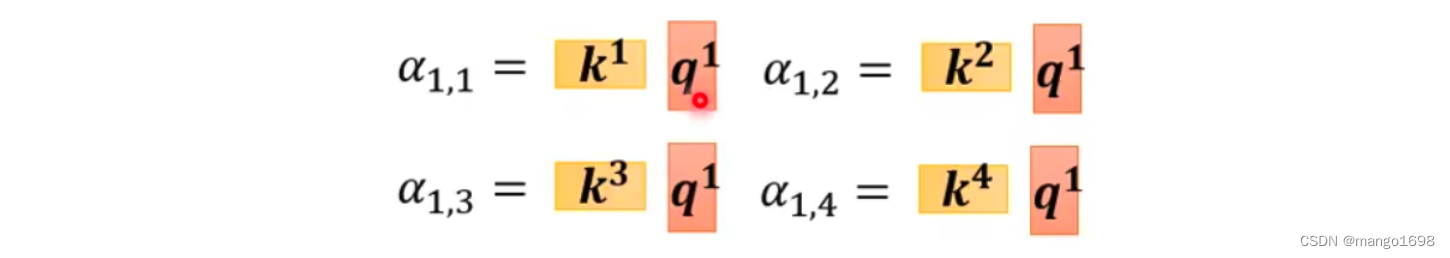
我们可以把 k 1 , . . . , k 4 k^1,...,k^4 k1,...,k4拼起来作为矩阵的4行,则
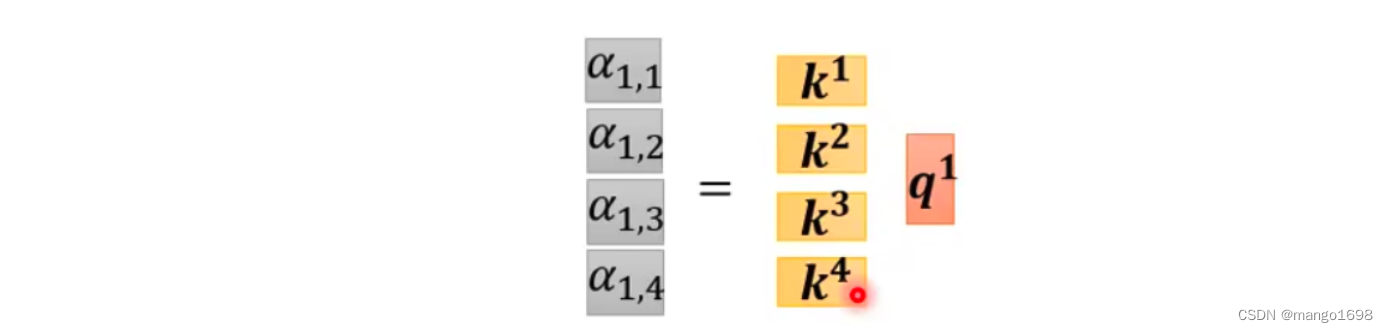
上面,仅仅是对 a 1 a^1 a1来求对应的 α \alpha α,那么对于全部的向量,则
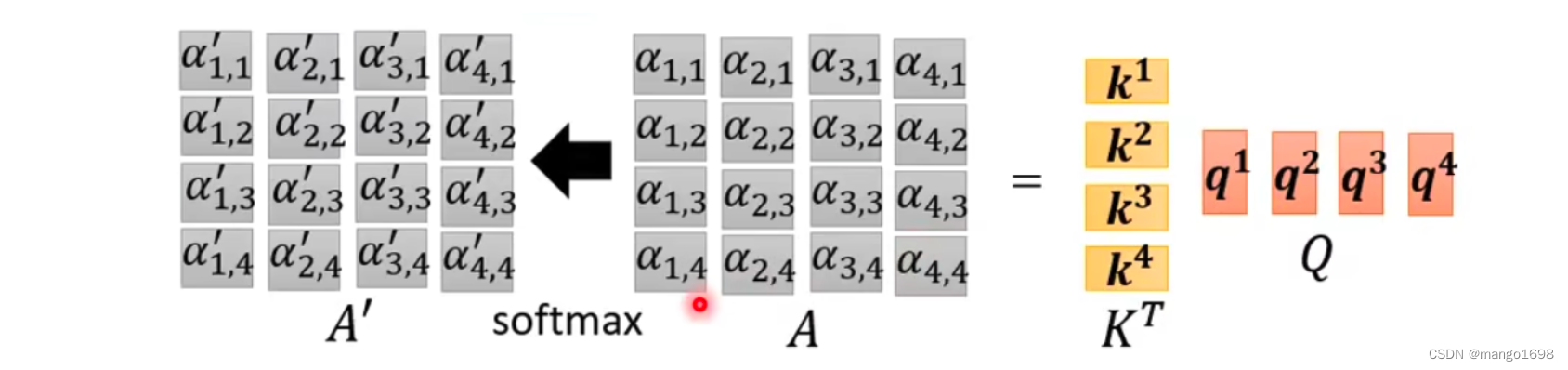
由此,上述过程,可以看作是两个矩阵相乘。即,可以写成 A = K T Q A = K^TQ A=KTQ
计算出 α ′ \alpha' α′后,然后分别乘以 v i v^i vi,然后相加,就可以得到最后的结果。即 O = V A ′ O = VA' O=VA′
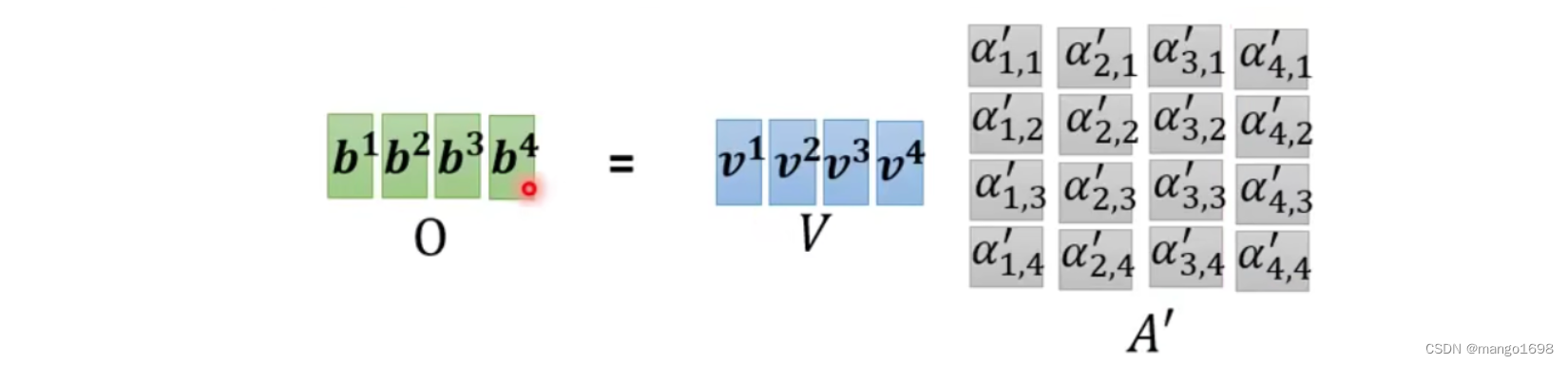
整体过程
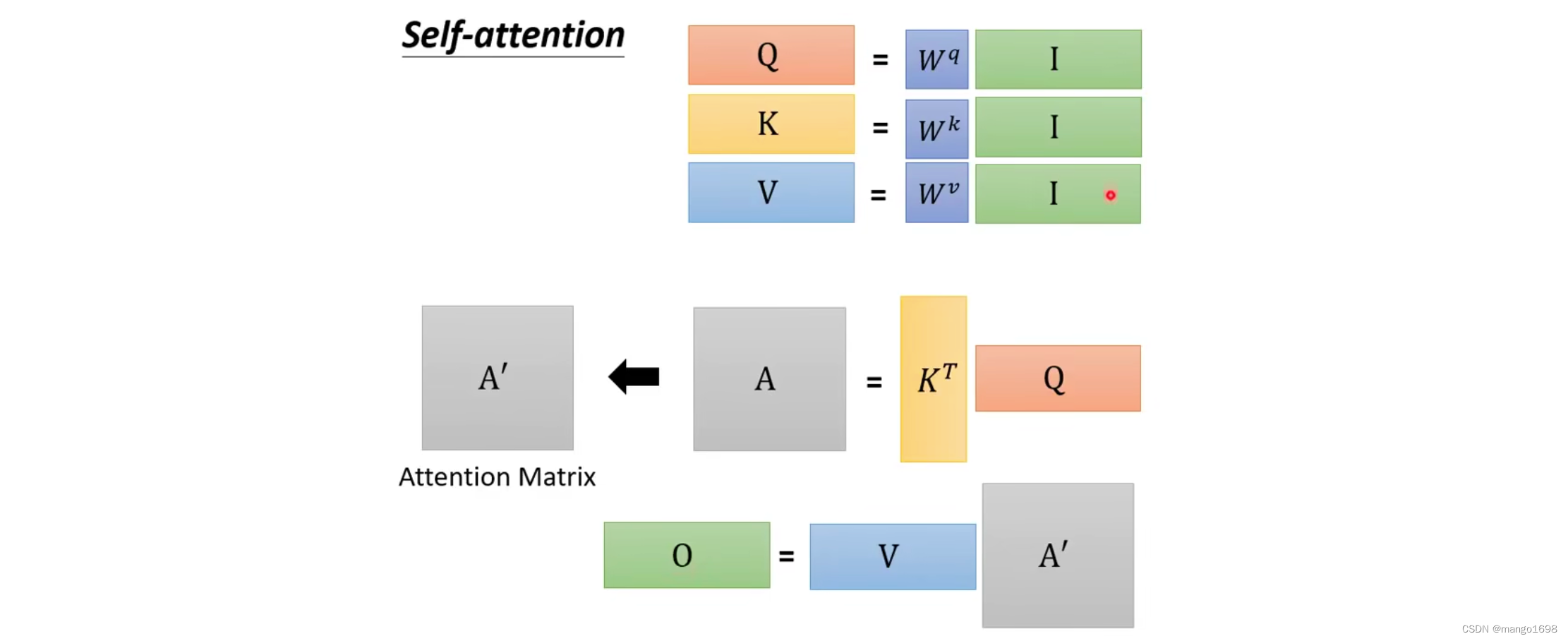
self-attention layer里面要学的参数仅仅为: W q , W k , W v W^q,W^k,W^v Wq,Wk,Wv。
2. Multi-head Self-attention
多头注意力机制。
是self-attention的一个进阶版本。
并不是所有的任务都适合用比较少的head,比如说翻译等,使用比较多的head可以得到比较好的结果。
使用多少个head,这是一个超参数,是需要调整的。
为什么需要多个head呢?相关这件事情,在做self-attention时,我们使用 q q q去找相关的 k k k。但是相关这一事情,有很多不同的形式。
所以,我们也许不能只有一个 q q q,我们应该有多个 q q q,不同的 q q q负责不同种类的相关性。
先让 a i a^i ai乘上矩阵 W q W^q Wq得到 q i q^i qi,然后在把 q i q^i qi乘上另外两个矩阵,得到 q i , 1 , q i , 2 q^{i,1},q^{i,2} qi,1,qi,2。同理,获得 k 和 v k和v k和v。对于其他位置,也是同理获得多个 q , k , v q,k,v q,k,v。
接下来,做self-attention的时候,1类的一起做,2类的一起做。
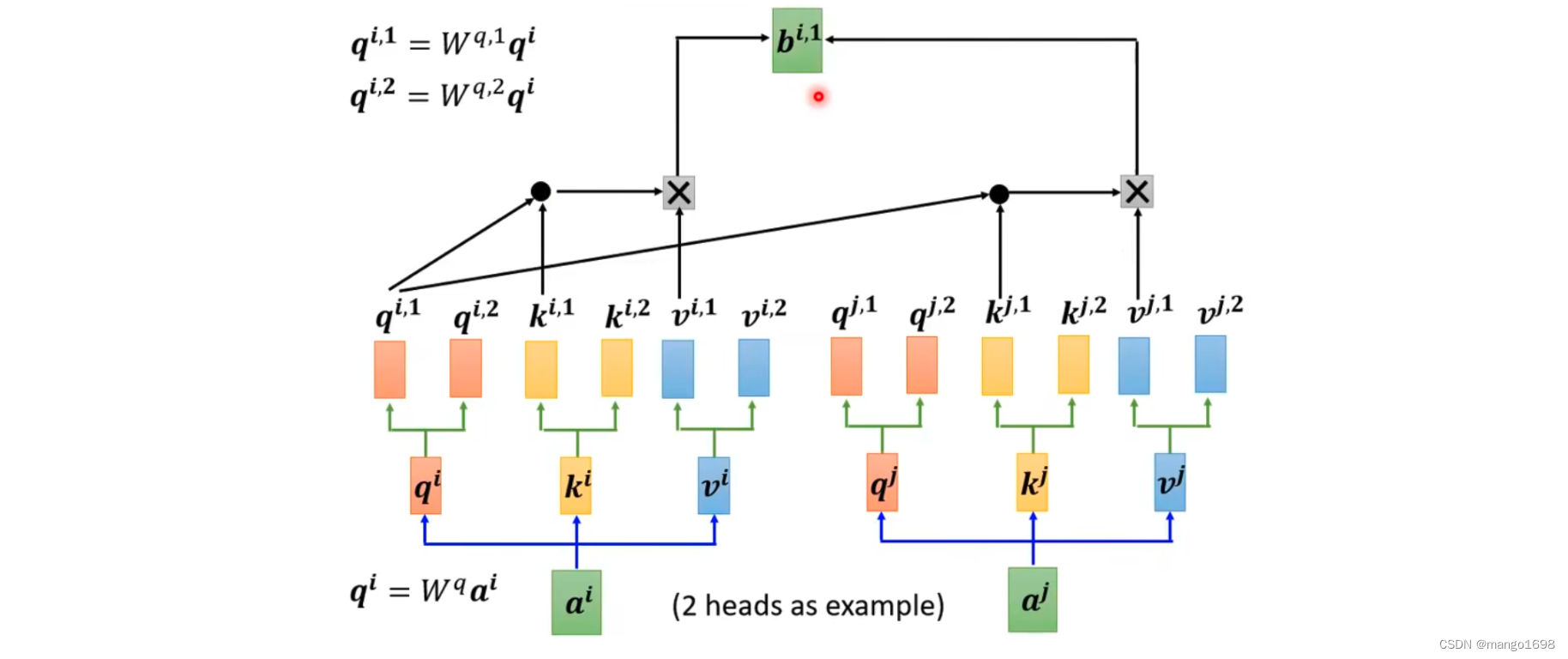
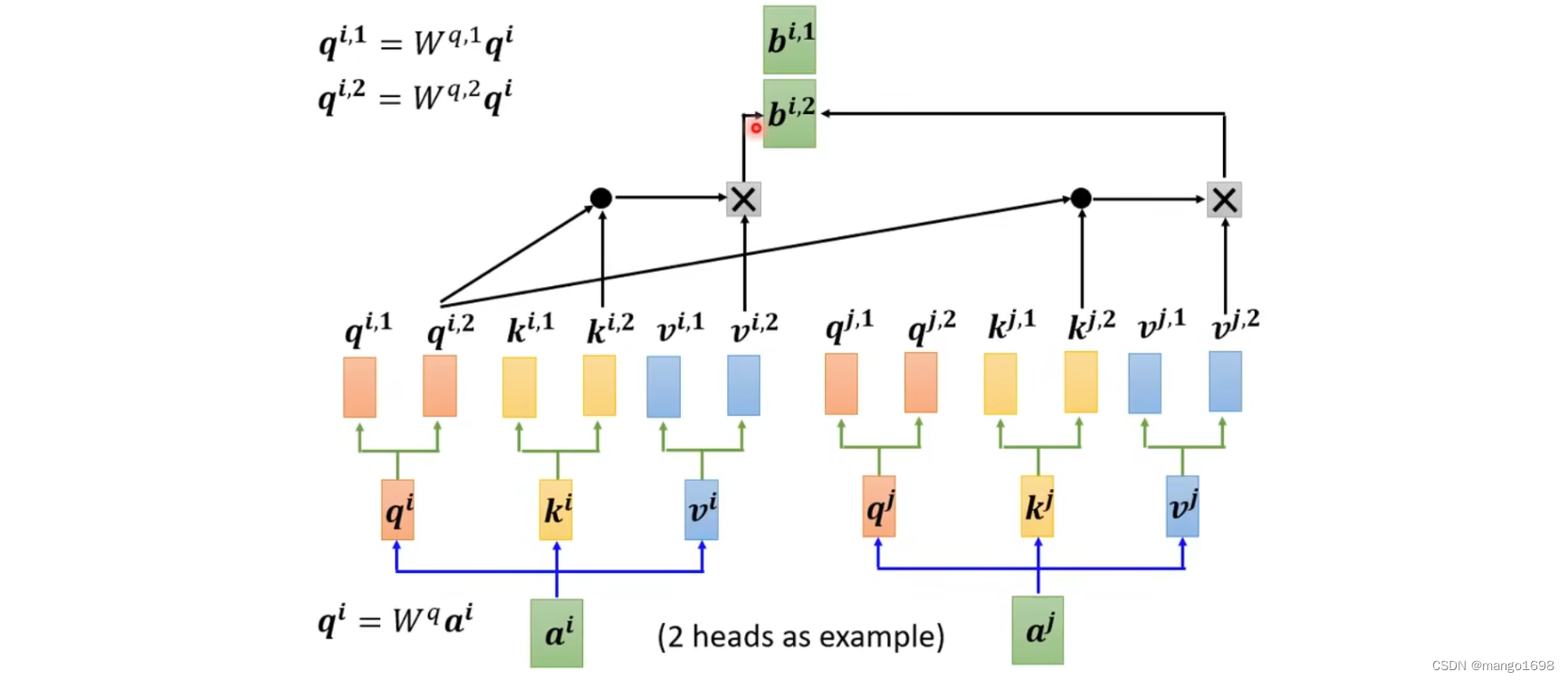
得到 b i , 1 和 b i , 2 b^{i,1}和b^{i,2} bi,1和bi,2后,将它们接起来,然后乘上一个矩阵得到 b i b^i bi,然后送到下一层。
3. Positional Encoding
self-attention这一层少了位置信息。
这样的设计,可能会有一些问题,有时候位置的信息很重要。
当我们在做self-attention的时候,如果我们觉得位置信息是非常重要的,那我们可以把位置的信息塞进去。
那怎么把位置的信息塞进去呢?
使用positional encoding技术。
为每个位置设置一个vector,叫做positional vector,使用 e i e^i ei进行表示。每个不同的位置有不同的vector。
把这个 e i e^i ei加到 a i a^i ai上面就可以了。
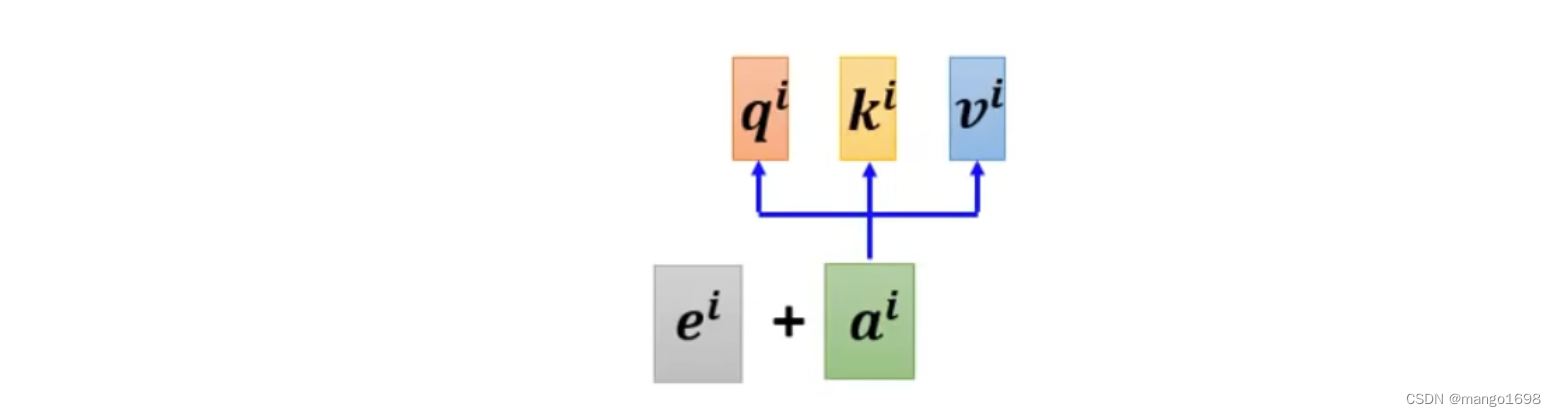
positional vector是手动设置的。
但是positional vector是可以通过学习获得的。
self-attention不是只可以用在NLP相关的应用上,它还可以用在其他的问题上。

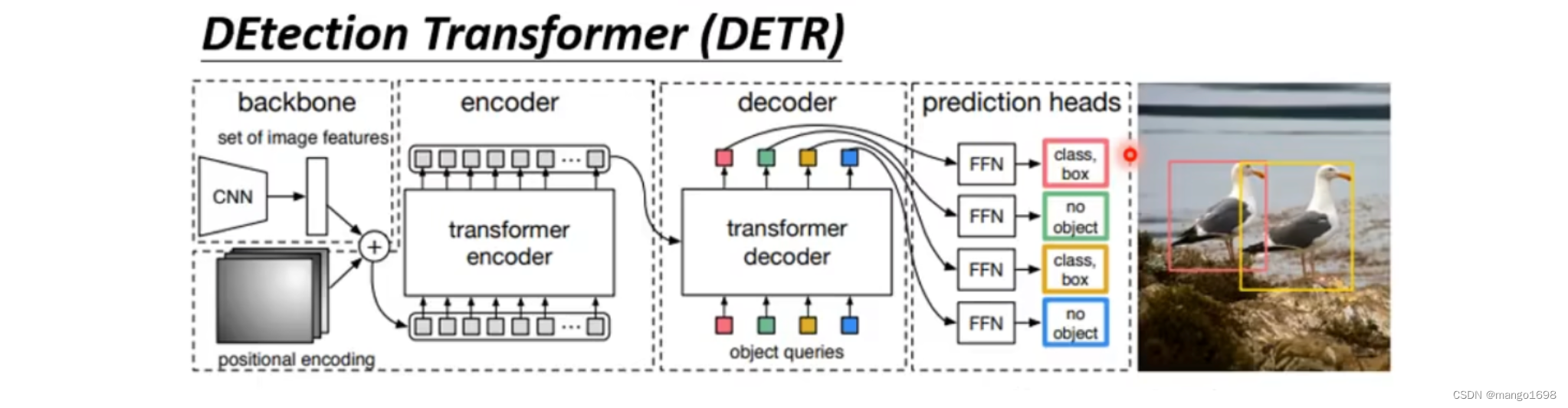
BERT(Bidirectional Encoder Representations from Transformers)和DETR(DEtection Transfomer)是两个不同领域的深度学习模型。
- BERT主要应用于自然语言处理(NLP)领域。它是一种预训练的语言模型,使用Transformer架构进行训练。BERT能够理解上下文关系,因为它是双向的(Bidirectional),能够同时考虑输入文本的前后文信息。BERT的预训练模型在多个NLP任务上表现出色,包括文本分类、命名实体识别、问答等。
- DETR则主要应用于计算机视觉领域,特别是目标检测。它采用了Transformer架构,但不同于传统的目标检测方法,DETR将目标检测任务转化为一个端到端的Transformer问题,消除了传统两阶段目标检测方法的需要。DETR在目标检测任务上取得了一些令人瞩目的成果。
在self-attention处理图像时
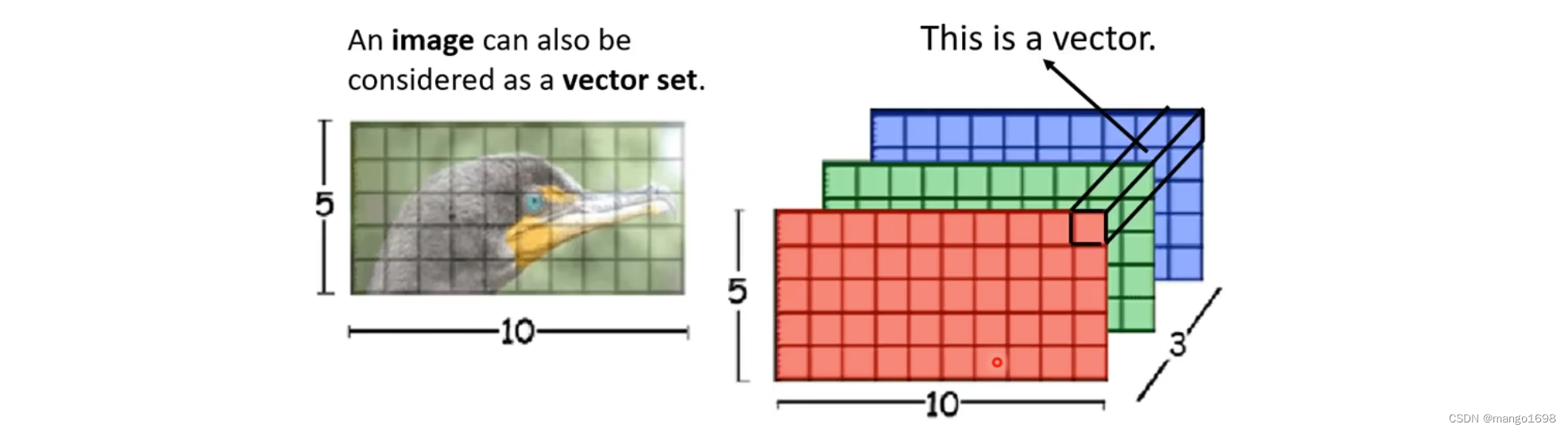
Self-attention v.s. CNN
CNN:可以看作是简化版的self-attention,只考虑临近区域的信息。
self-attention:考虑整张图片的信息。
4. Transformer
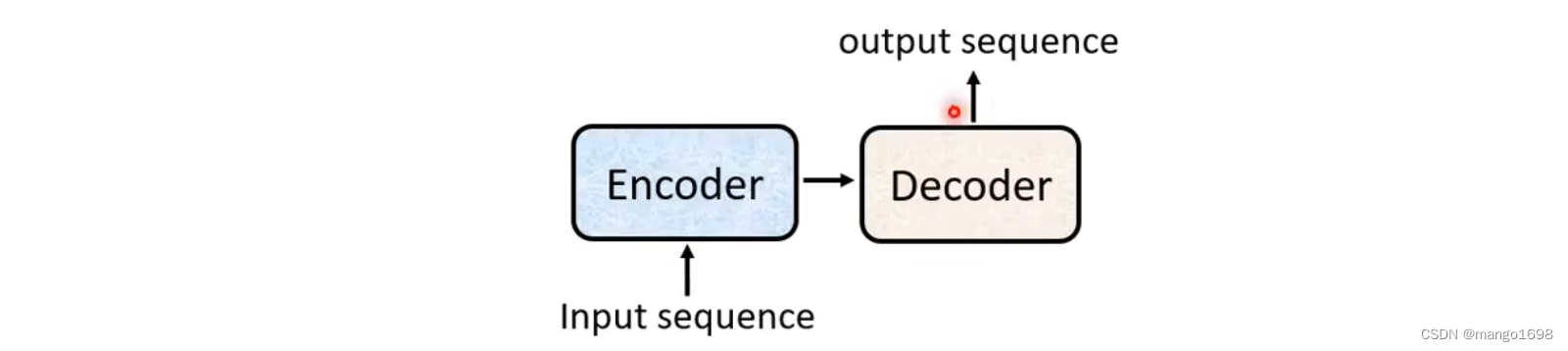
Transformer是Sequence-to-sequence(Seq2seq)的model。
Sequence-to-sequence:输入是一个sequence,输出是一个sequence,但是我们不知道输出的长度,由机器自己决定输出的长度。
如:语言辨识,翻译等。
Seq2seq可以分为两块:Encoder和Decoder。
4.1 Encoder
encoder做的就是输入一排向量,输出一排向量。
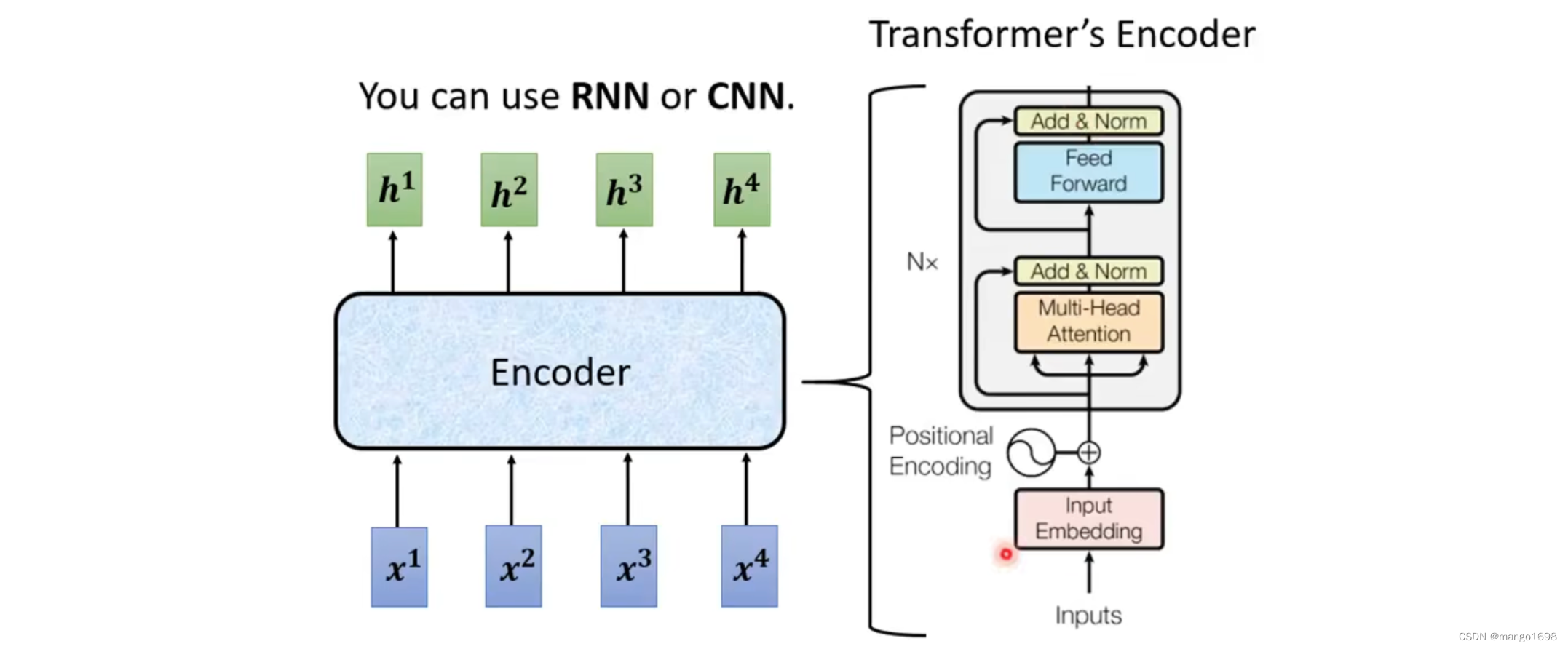
Encoder里面会分为很多block,每个block输入一排向量,输出一排向量。每个block是好几个layer组成。
在transformer的encoder里面:每个block,先做self-attention,然后经过全连接层。
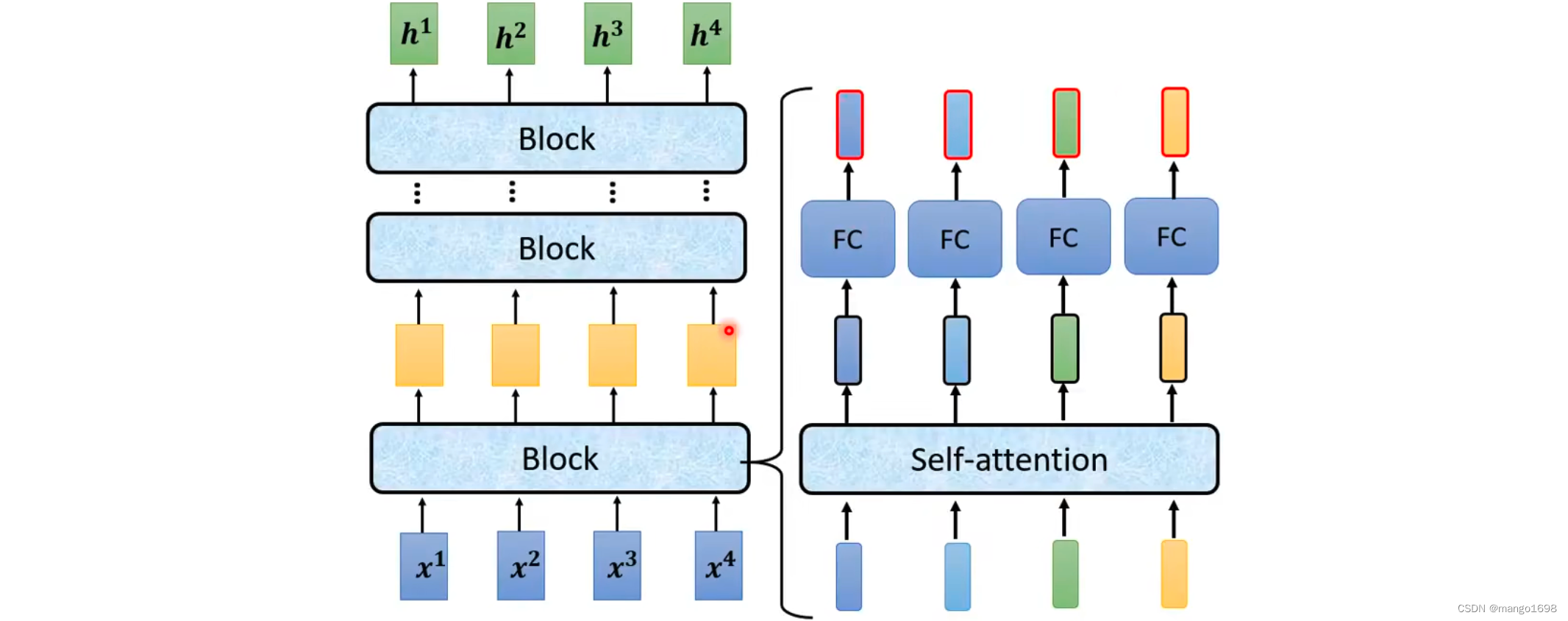
在原Transformer中做的是更复杂的。
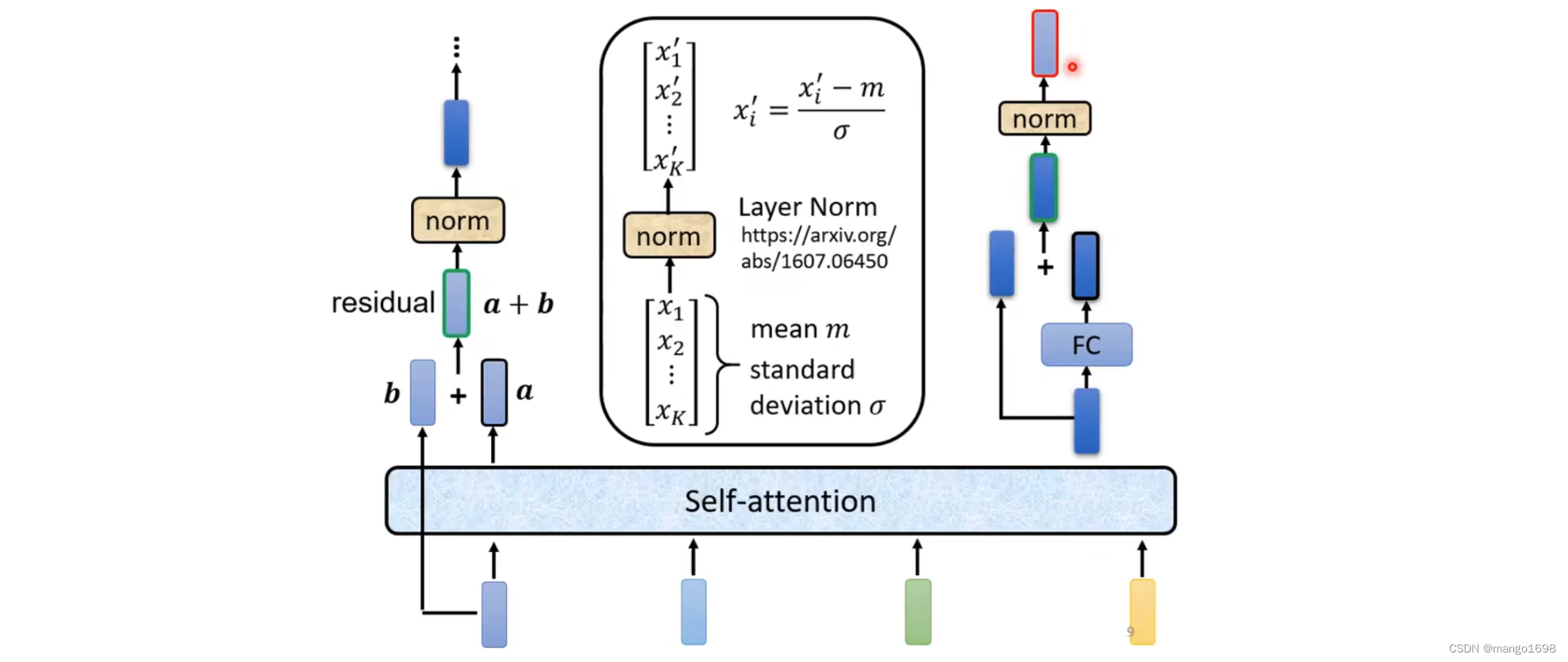
在Transformer中,加入了一个设计,经过self-attention后,输出一个向量,我们要把输出的这个向量与它本身输入相加,得到输出。这样的操作叫做residual connection。
得到输出后,再将输出进行Layer Normalization。Layer Normalization不需要考虑batch。Layer Normalization计算输入向量的平均值和标准差,Layer Normalization对同一个feature,同一个example里面,不同的dimension去计算平均值和标准差。计算出平均值和标准差后做Normalization。得到Normalization的输出,这个输出才是全连接层的输入。
全连接层也使用了residual connection的架构。经过redisual后,将输出再做一次layer normalization,得到的输出才是一个block的输出。
4.2 Decoder
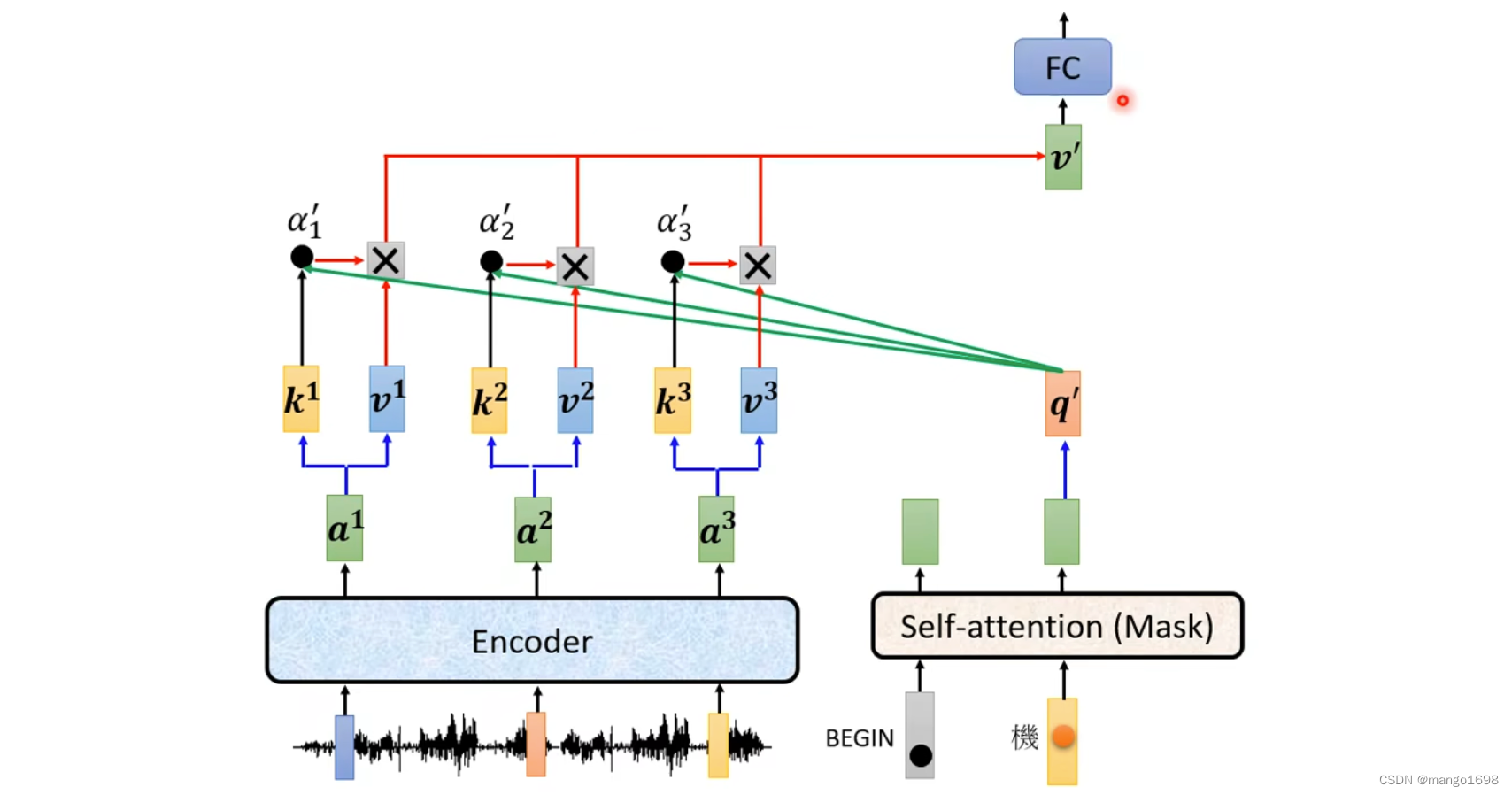
decoder要做的就是产生输出。其要先读入encoder的输出。
Decoder分为两种:Autoregressive(AT)和Non-autoregressive(NAT)。
4.2.1 Autoregressive
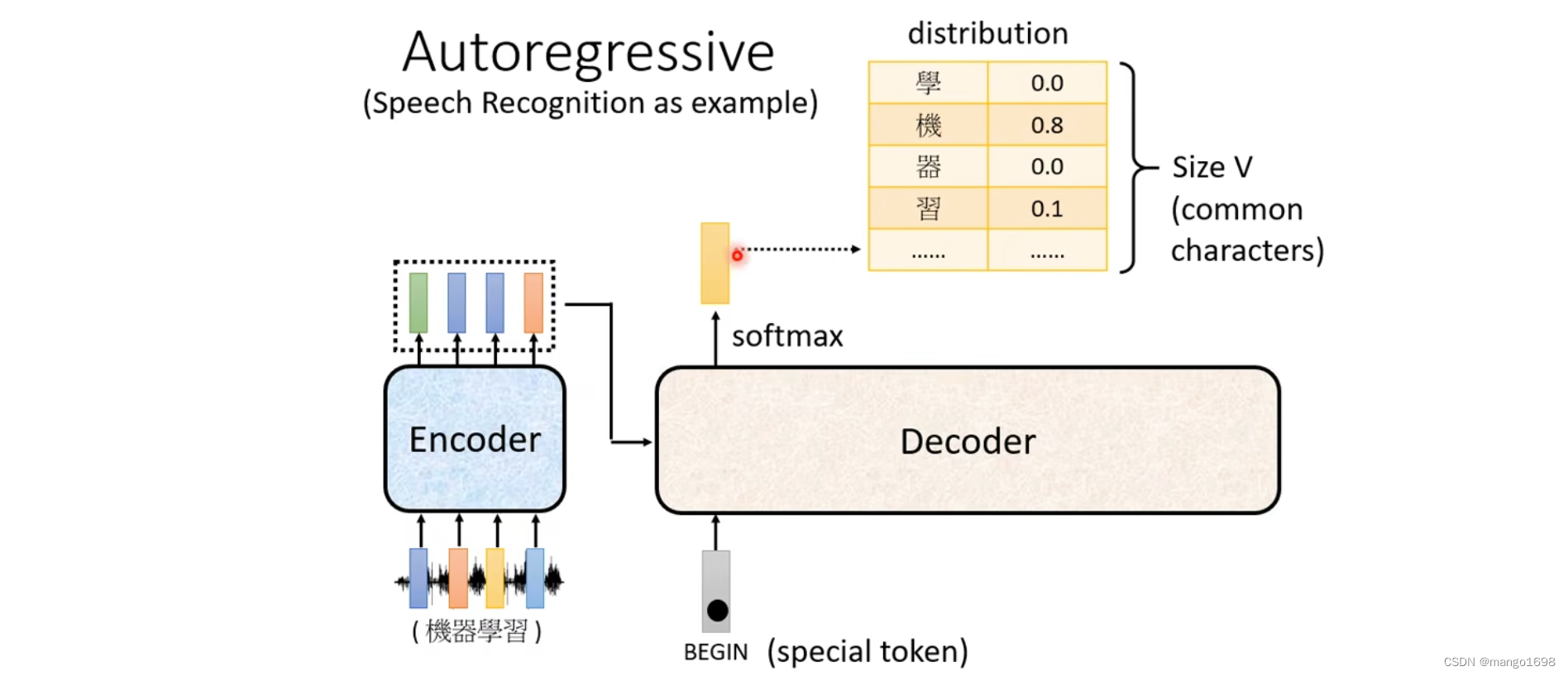
对于语音识别,Decoder怎么能产生一段文字呢?
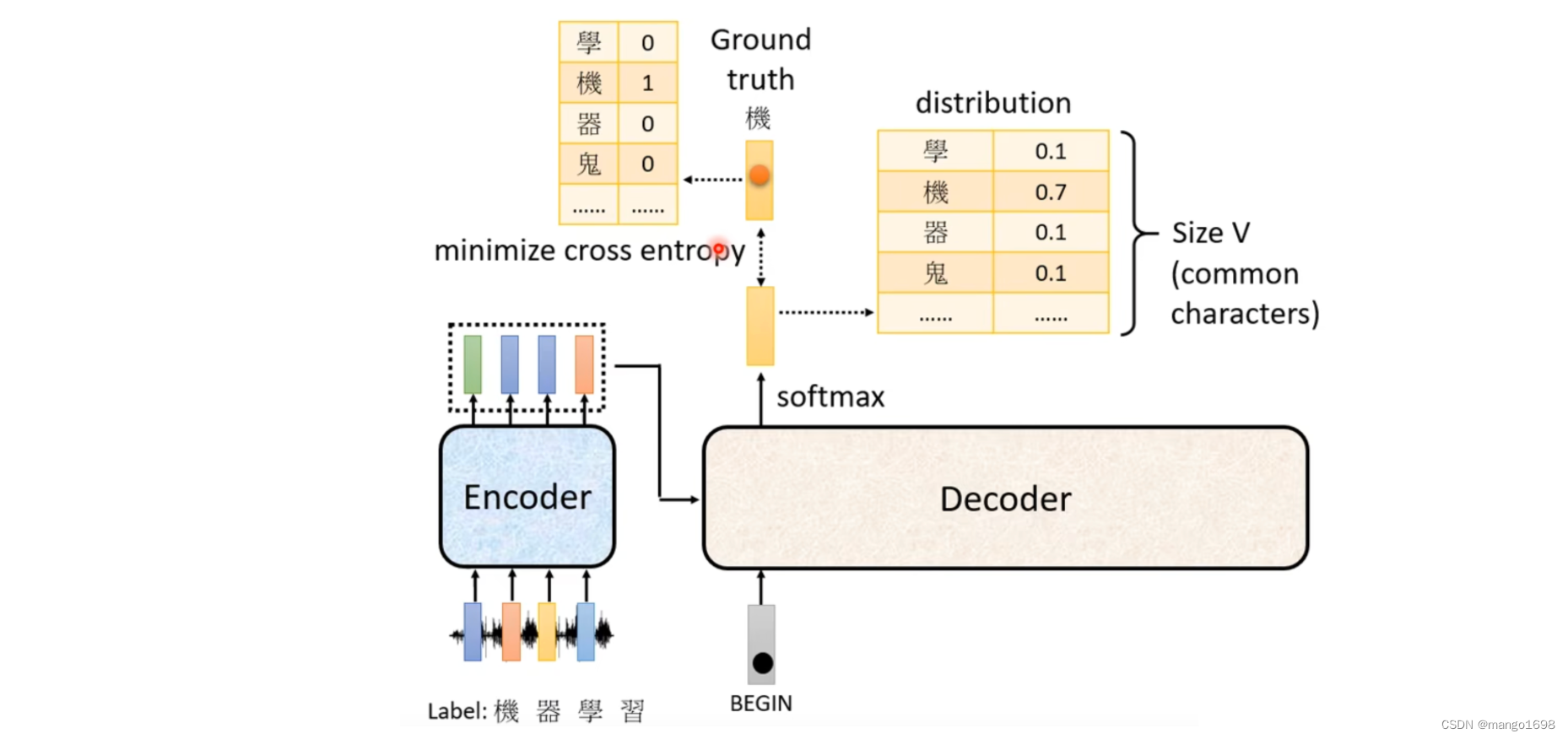
首先给decoder一个特殊的符号,这个特殊的符号代表开始BOS(special token)。在decoder本来可能产生的文字里面多加一个特殊的字,这个字就代表了开始begin。得到一个输出向量,这个向量的长度,对于中文来说,可能就是汉字的数量。每一个字都会对应到一个数值,值最高的对应的字就是最终的输出。比如机这个字。
然后将出了将begin作为输入外,还将机作为decoder的输入,然后得到一个输出,器。然后再将器也作为输入,最后输出学。然后再将学也作为输入,最后输出习。
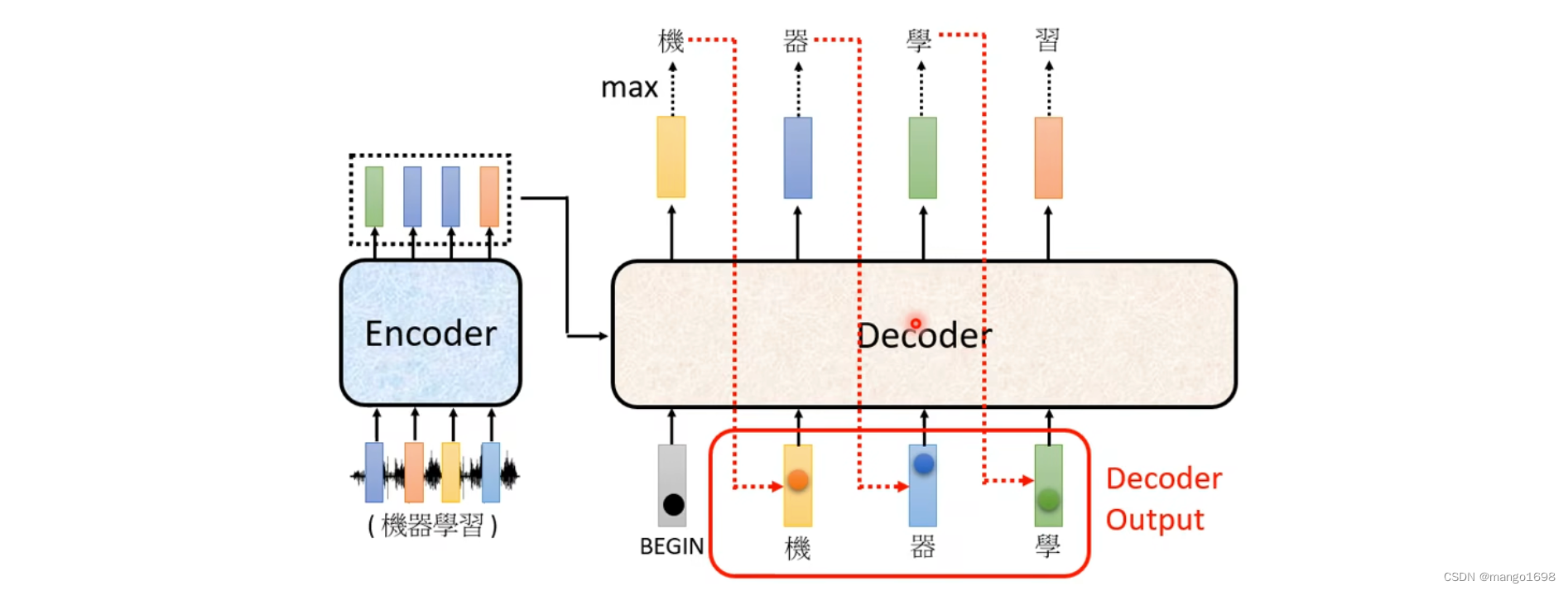
decoder得到的输入,其实是它在前一个时间点自己的输出。也就是说,decoder可能会得到一个错误的输入。那这样可能会造成一步错步步错的问题。
decoder结构
在transformer中,decoder的结构:
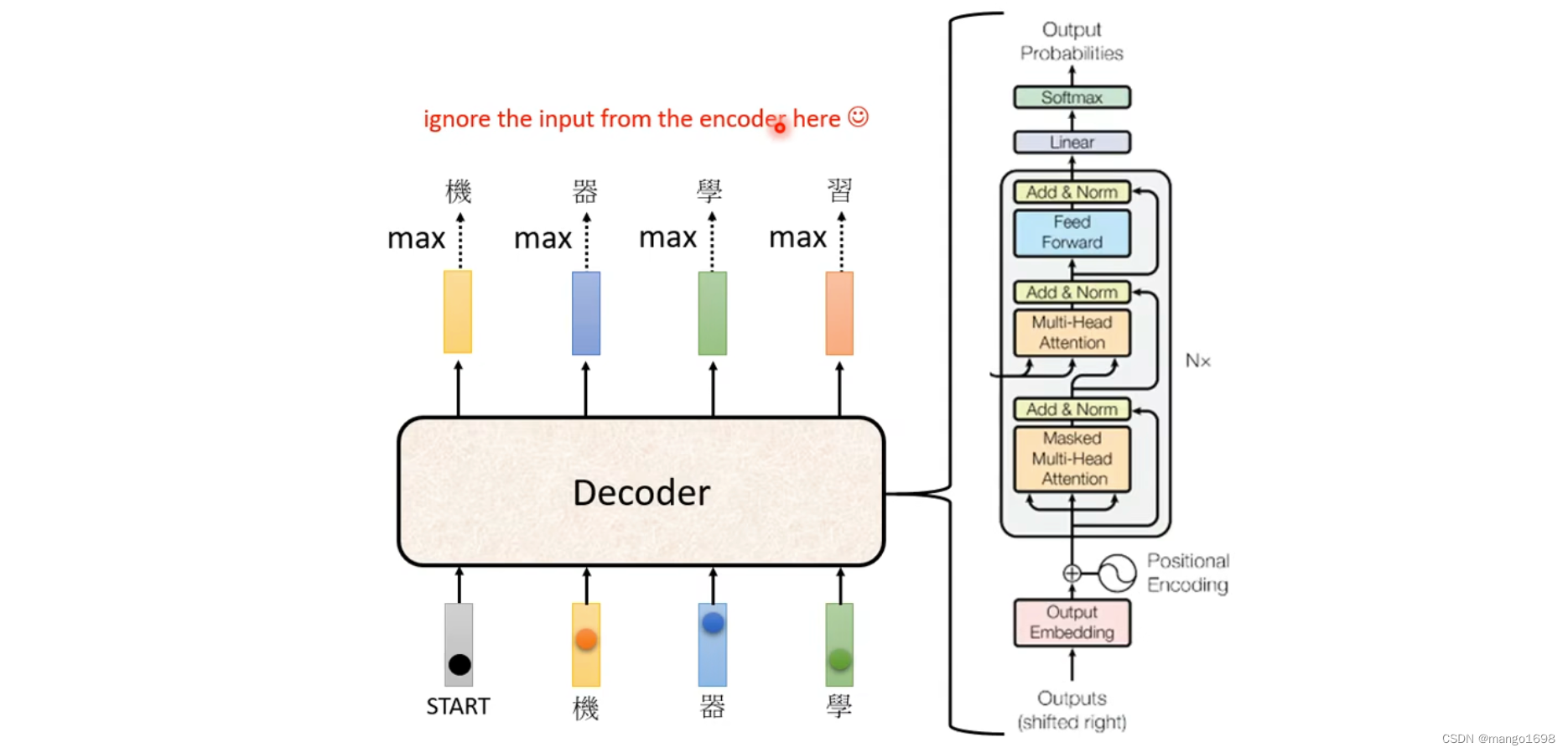
从self-attention到Masked Self-attention
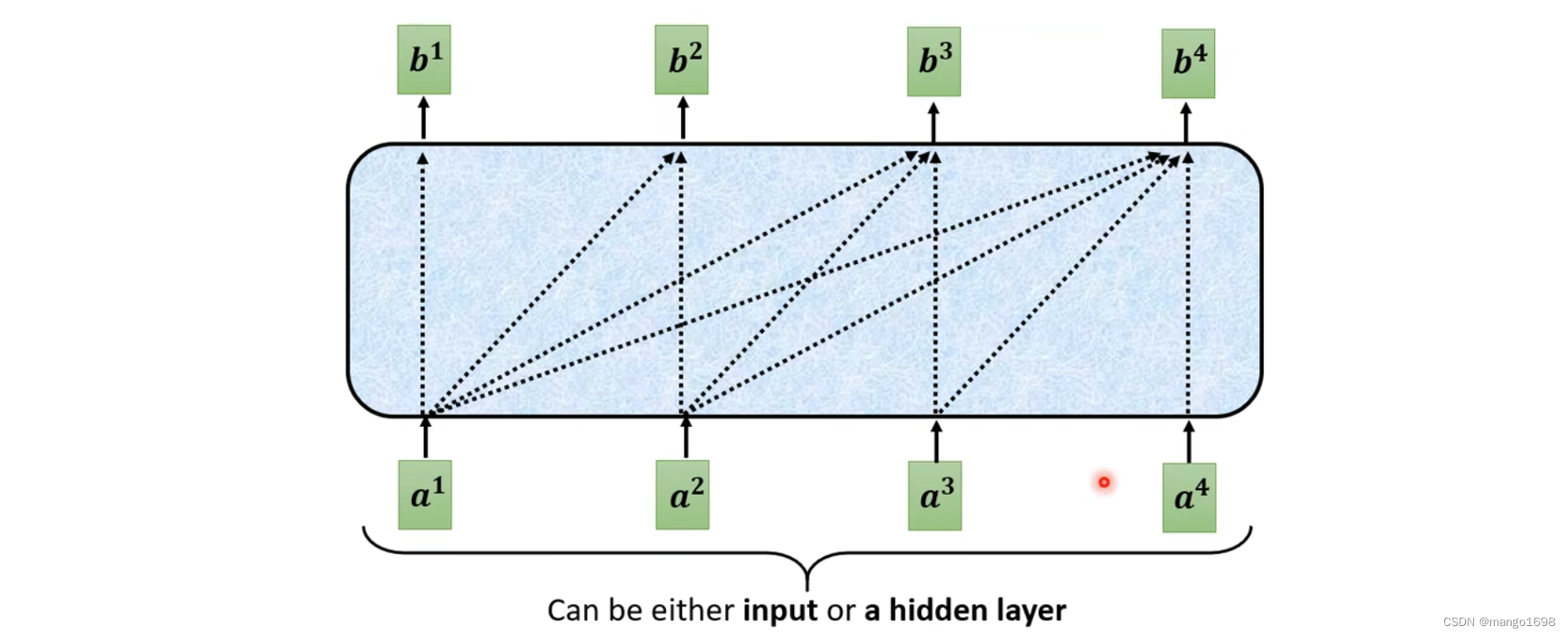
也就是,产生 b 1 b^1 b1的时候,只能考虑 a 1 a^1 a1的信息,产生 b 2 b^2 b2的时候,只能考虑 a 1 , a 2 a^1,a^2 a1,a2的信息。以此类推。
更具体一点:比如在计算 b 2 b^2 b2的时候,只用 a 2 a^2 a2的 q 2 q^2 q2与 k 1 与 k 2 k^1与k^2 k1与k2进行计算不需要去管其他的k。
那为什么需要加masked呢?
因为decoder的运作方式,输出是一个一个产生的,先有 a 1 ,再有 a 2 ,再有 a 3 . . . a^1,再有a^2,再有a^3... a1,再有a2,再有a3...
原来的self-attention,
a
1
?
a
4
a^1-a^4
a1?a4是一次性整个输入到模型里面的。也就是说,对于Mask self-attention,在计算
b
2
b^2
b2的时候
a
3
,
a
4
a^3,a^4
a3,a4还不存在,所以没有办法让其参与进来。
还有一个非常关键的问题,decoder必须自己决定输出的序列的长度。也就是说,对于上面的例子,可能输出习之后,可能又将习作为新的输入,然后再输出惯,然后一直进行下去…
所以,我们要让decoder输出一个断,我们需要准备一个特殊的符号,用End来表示。
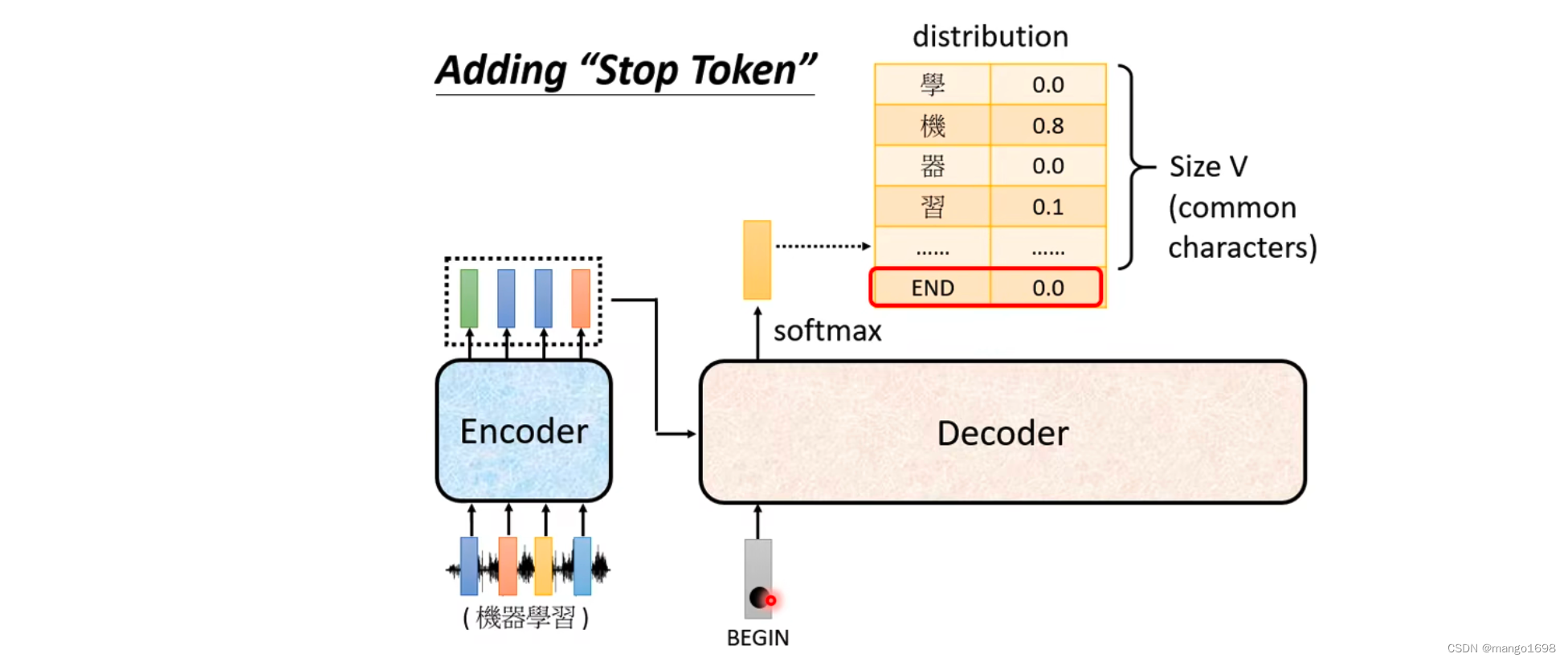
这样,当输出习之后,再将习作为新的输入,这时输出应该得到End。然后整个encoder的运作过程就结束了。
4.2.2 Non-autoregressive
NAT不是一次产生一个字,而是一次把整个句子产生出来。
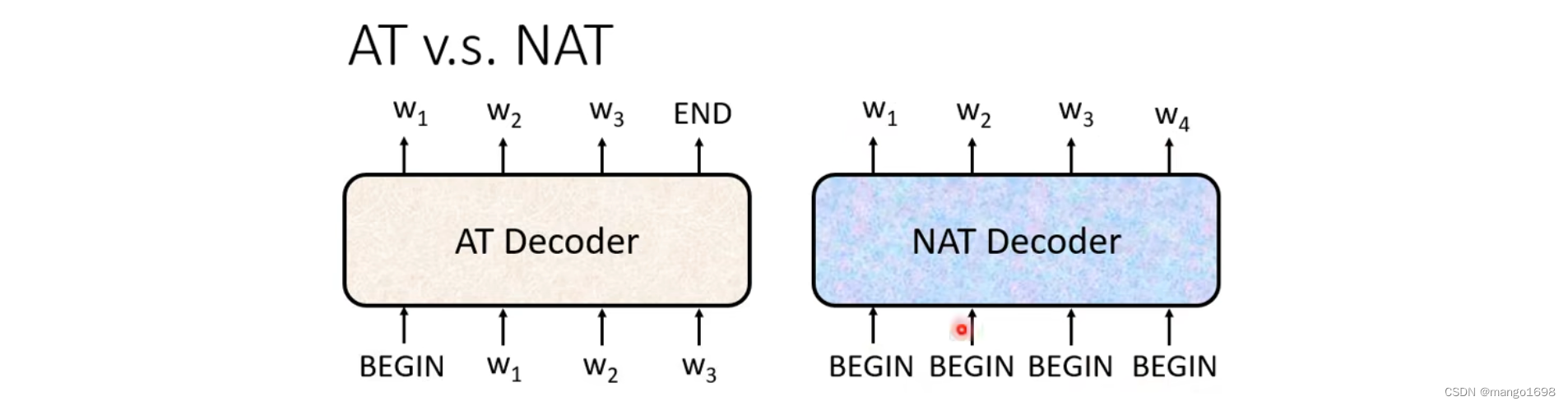
但是,我们不是不知道输出的长度说多少吗?那begin该给多少个呢?
解决方法:
- 另外设置一个分类器,这个分类器将encoder的输出作为输入,输出是数字,这个数字代表encoder应该要输出的长度。
- 给它一堆begin,假设这个句子的长度绝对不会超过300个字,那就给它300个begin,然后看其什么地方输出了
End,然后将后面的输出忽略掉。
NAT的优点
- 并行化 。
- 可以控制输出的长度。
4.3 Encoder-Decoder
encoder与decoder连接。
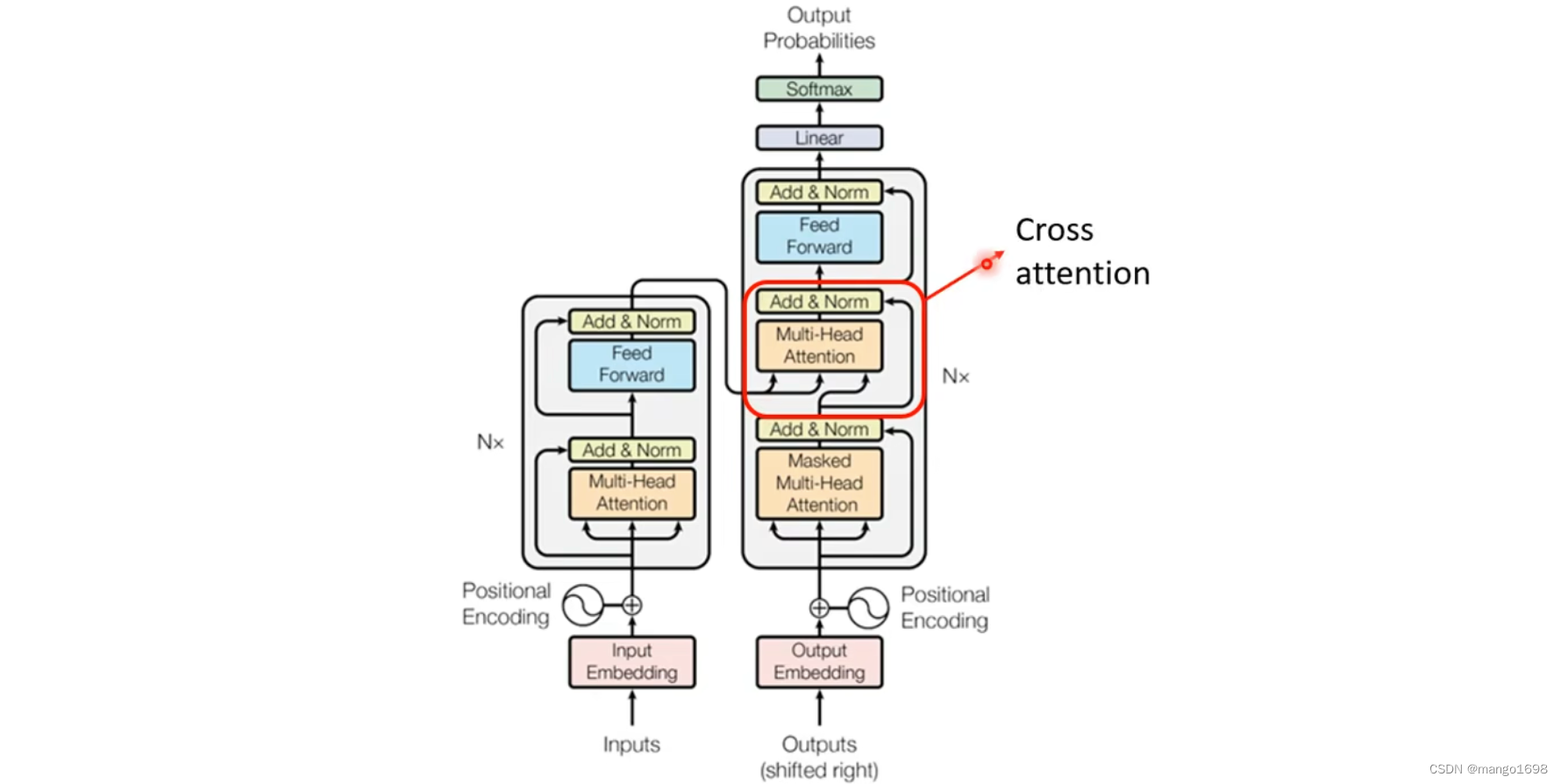
Cross attention的两个输入来自于encoder,一个输入来自于decoder。
4.4 Training
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!