代码随想录算法训练营Day17 | 530.二叉搜索树的最小绝对差、501.二叉搜索树中的众数、236.二叉树的最近公共祖先
发布时间:2024年01月04日
LeetCode 530 二叉搜索树的最小绝对差

本题思路:看到二叉搜索树,我们可以知道,它的中序遍历的有序的。并且是单调递增。如下图所示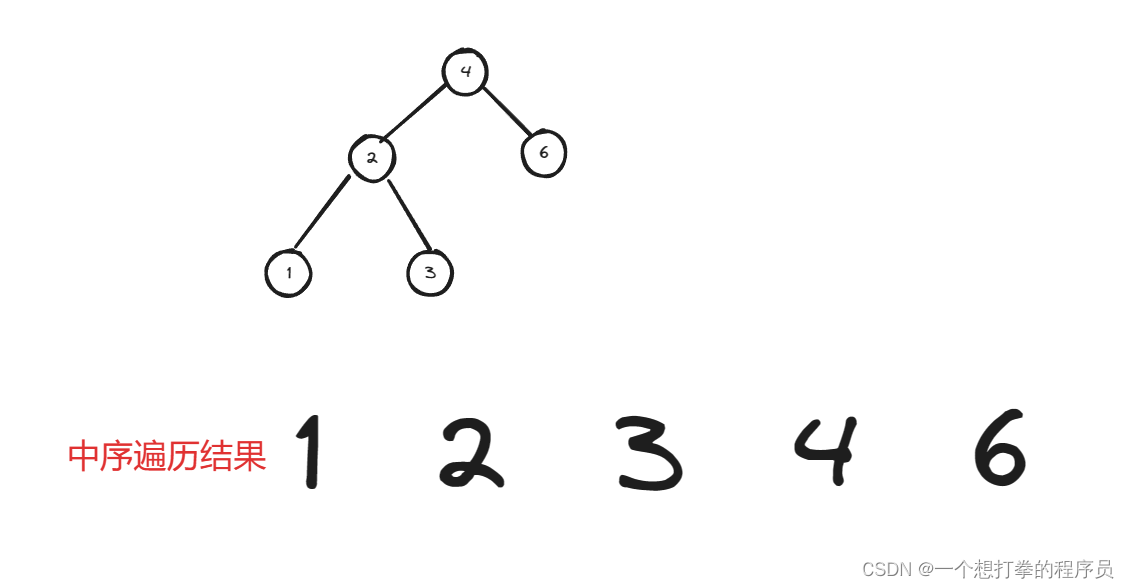
然后我们就可以计算出相隔的两个数之间的差值,然后找到最小的那一个即可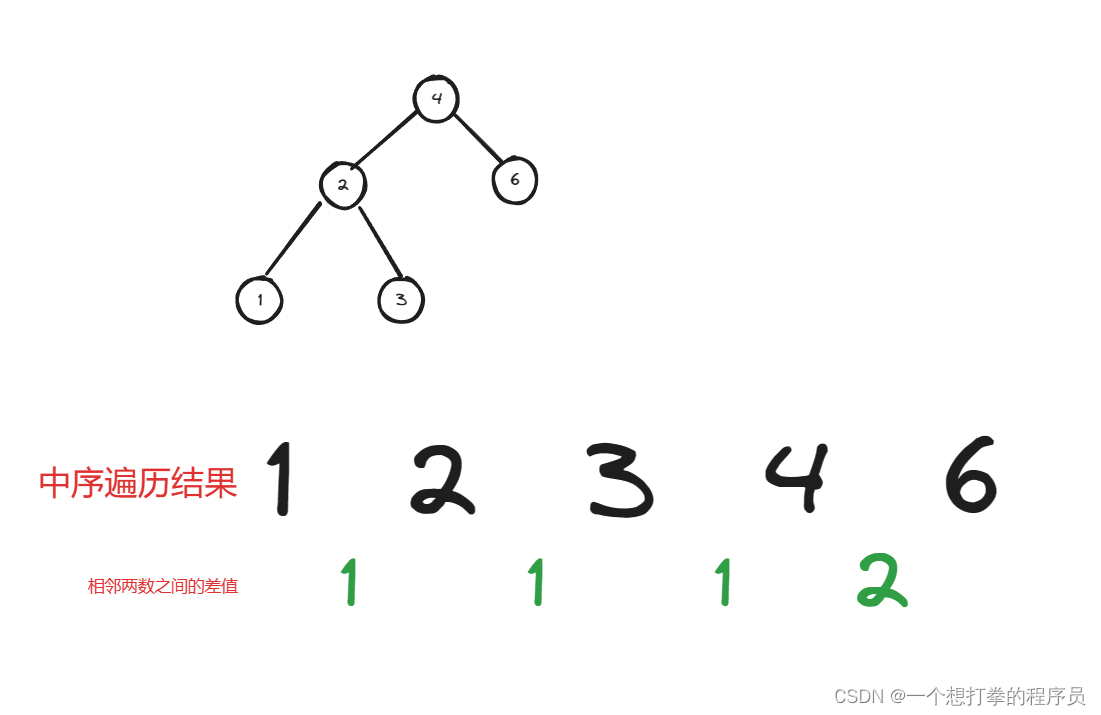
定义一个初始为 min = 第二个元素 - 第一个元素。然后从第三个元素开始计算,如果发现差值 小于等于 min,就替换 min,遍历结束后,就得到了最小的 min 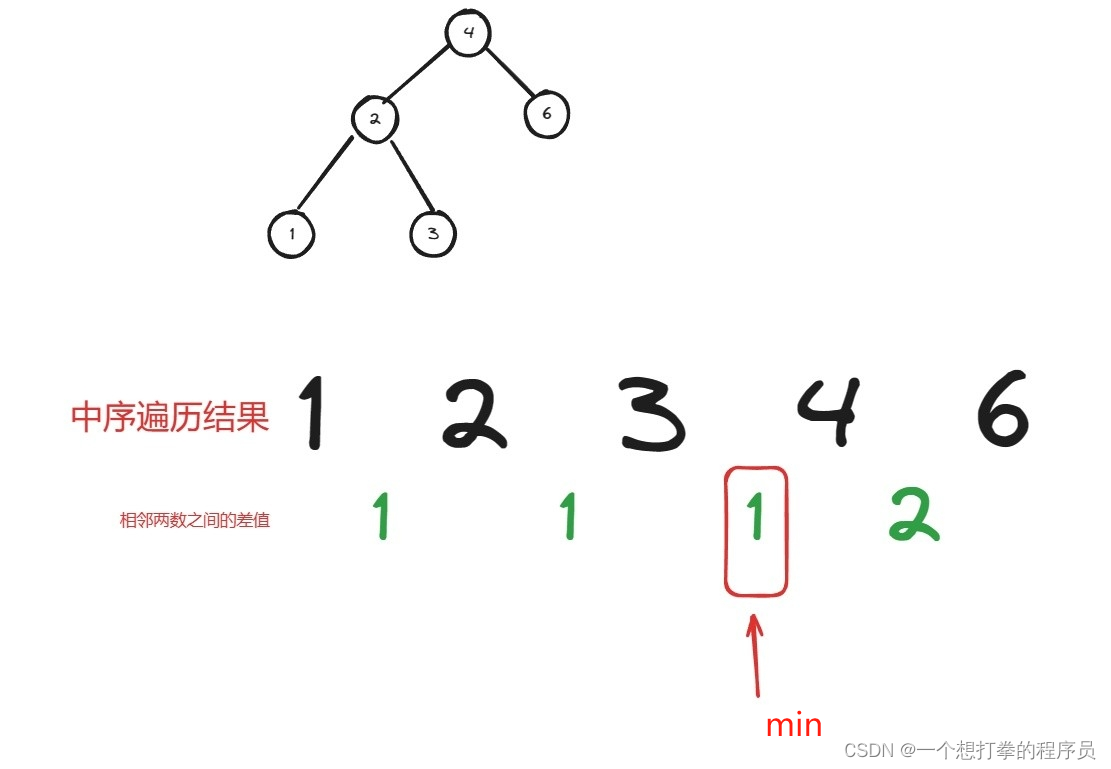
看到搜索树,我们要想到中序遍历的结果,是有序的。
class Solution {
public int getMinimumDifference(TreeNode root) {
List<Integer> list = new ArrayList();
inorder(root,list);
int min = list.get(1)-list.get(0);
for(int i = 1; i < list.size(); i++){
if((list.get(i) - list.get(i-1)) <= min){
min = (list.get(i) - list.get(i-1));
}
}
return min;
}
public void inorder(TreeNode root, List<Integer> list){
if(root == null){
return;
}
inorder(root.left,list);
list.add(root.val);
inorder(root.right,list);
}
}
LeetCode 501 二叉搜索树中的众数
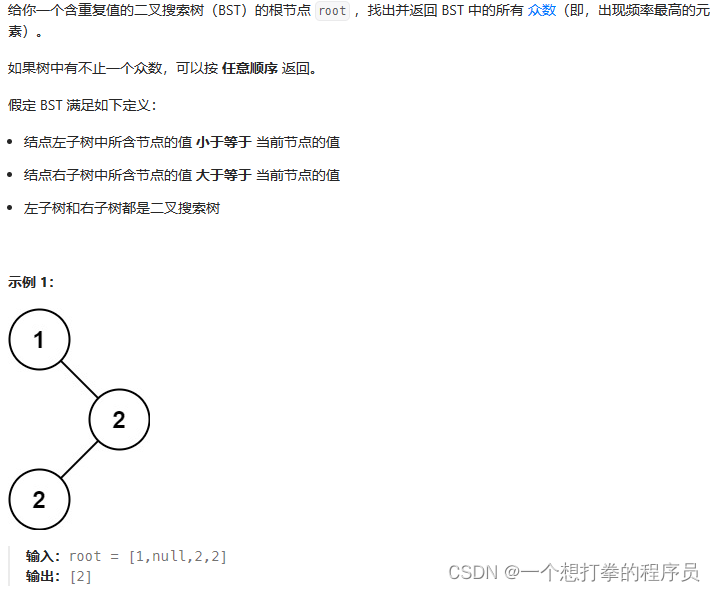
本题思路: 这道依旧是通过中序遍历,得到一个有序的列表,如下图所示
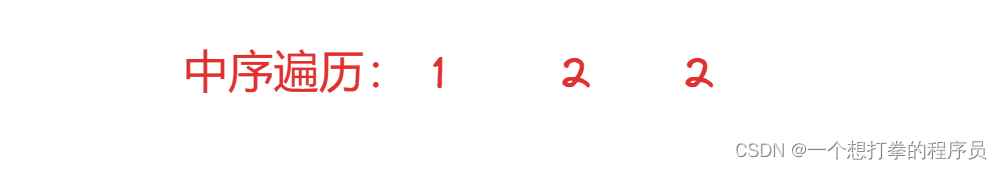
然后通过一个 map 集合,将每个数,出现过的次数存起来,Key:值本身,Value:出现的次数
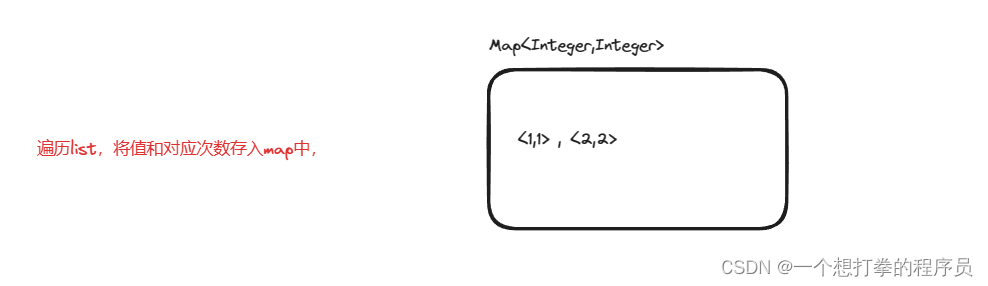
然后通过一个队列,将出现次数大的放进去,并且相同的放进去。如果遇到更大的,就清空原来的队列,放入新的大元素。
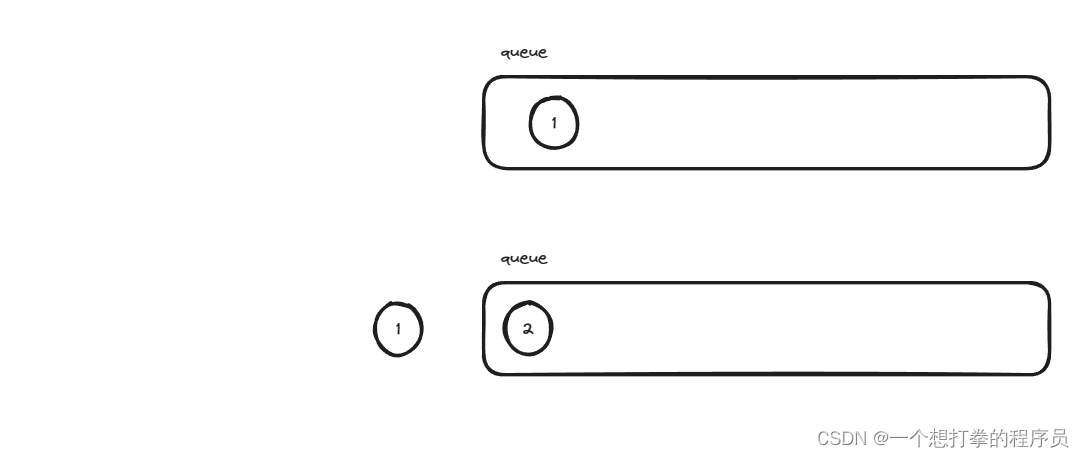
class Solution {
public int[] findMode(TreeNode root) {
List<Integer> list = new ArrayList();
inorder(root,list);
Map<Integer,Integer> hashMap = new HashMap();
for(int i = 0; i < list.size(); i++){
hashMap.put(list.get(i),hashMap.getOrDefault(list.get(i),0) + 1);
}
Deque<Integer> deque = new ArrayDeque();
int max = -1;
for(Map.Entry<Integer,Integer> map : hashMap.entrySet()){
int key = map.getKey();
int value = map.getValue();
if( value == max){
deque.addLast(key);
}
if( value > max){
deque.clear();
deque.addLast(key);
max = value;
}
}
int[] ans = new int[deque.size()];
for(int i = 0; i < ans.length; i++){
ans[i] = deque.removeFirst();
}
return ans;
}
public void inorder(TreeNode root, List<Integer> list){
if(root == null){
return;
}
inorder(root.left,list);
list.add(root.val);
inorder(root.right,list);
}
}
LeetCode 236 二叉树的最近公共祖先

本题思路:找最近的公共祖先,那么应该是自底向上来寻找。所以我们可以用后序遍历来完成。
- 递归的第一步就是找出口,有以下几种情况
- 第一种情况,root 为空节点的时候,直接返回 null 即可
- 第二种情况如下图,root == q || root = p,直接返回 root,找到了
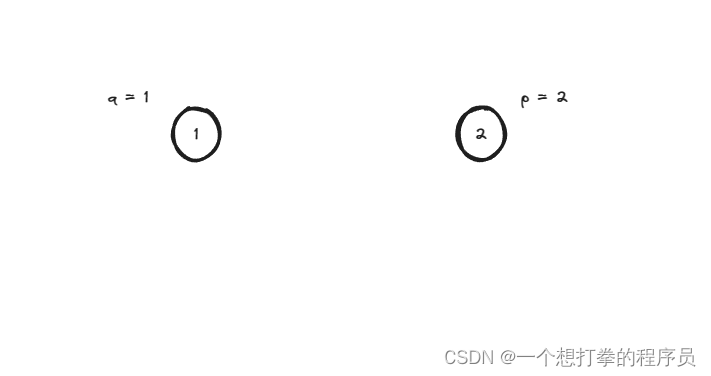
- 然后就开始在 root(节点2) 的左树中,查找是否有 p 或者 q,假设如下图情况所示,
- 此时 root.left == q,直接返回 q
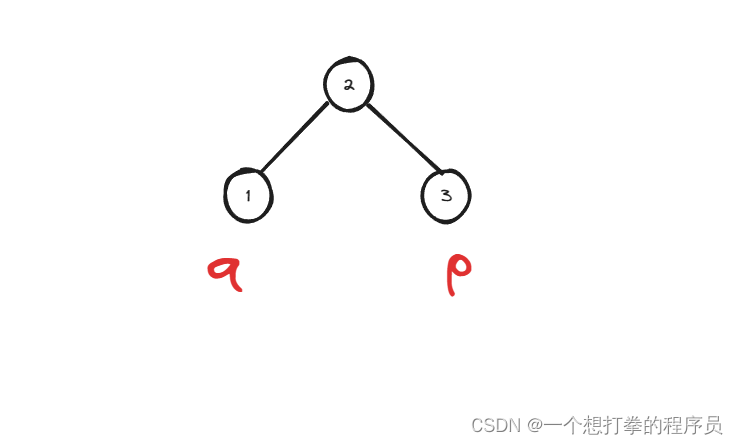
- 此时 root.left == q,直接返回 q
- 然后开始在 root(节点2)的右树中,查找是否有 p 或者 q,假设如下图所示
- 此时 root.right == p,直接返回 p
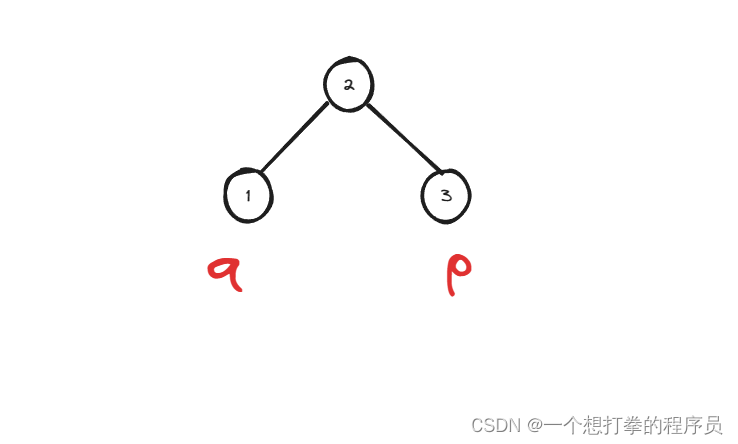
- 此时 root.right == p,直接返回 p
- 最后 left 和 right 都不为空,直接返回 root,节点二就是最近的公共祖先
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null){
return root;
}
if(root == p || root == q){
return root;
}
TreeNode left = lowestCommonAncestor(root.left,p,q);
TreeNode right = lowestCommonAncestor(root.right,p,q);
if(left ==null && right ==null){
return null;
}else if(left == null && right != null){
return right;
}else if(right == null && left != null){
return left;
}else{
return root;
}
}
}
文章来源:https://blog.csdn.net/hero_jy/article/details/135371619
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 适用于各种危险区域的火焰识别摄像机,实时监测、火灾预防、安全监控,为安全保驾护航
- MySQL--数据类型(4)
- 匹配excel表格中两列数据
- windows环境下cmd找不到pip
- 如何查看Linux CPU占有率
- 最简单的SpringBoot(3.0)的自动配置原理教程,看完不白雪!
- 关于Access中列的冻结的知识,看这篇就够了
- 【Spring Security】打造安全无忧的Web应用--使用篇
- yolov8人脸识别-脸部关键点检测(代码+原理)
- Spring Boot简单多线程定时任务实现 | @Async | @Scheduled