排序-快速排序

---

1、概念

快速排序（Quick Sort），是计算机科学与技术领域中非常经典的一种排序算法，应用分治思想进行排序。快速排序由于其时间复杂度优于大部分的排序算法，因而命名为快速排序。快速排序实现的核心思想就是在待排序序列中选择一个基准值，然后将小于基准值的数字放在基准值左边，大于基准值的数字放在基准值右边，然后左右两边递归排序，整个排序过程中最关键部分就是寻找基准值在待排序序列中的索引位置。

如：

每次选择一个基准值来划分，最后划分到不能划分为止，运用了分治的思想

2、选择基准值

我们可以选择第一个元素当基准值，但是如果遇到的是有顺序的数组的话，每次划分都会将数组剩余的元素划分到一边，并且每次都是一样，这样的的话就会降低快速排序的效率，因此我们为了解决这个问题，用了一个三数取中法，就是从首个元素，中间元素，最后一个元素中选择一个中间值作为基准值，这样的话就可以避免这个问题了。
代码实现：

//三数取中
int GetMidIndex(int* a, int left, int right) {
	int mid = (left + right) >> 1;//除2，找到中间元素下标、
	//进行三数对比，返回中间值
	if (a[mid] > a[left])
	{
		if (a[right] > a[mid])
			return mid;
		else if (a[right] > a[left])
			return right;
		else
			return left;
	}
	else 
	{
		if (a[left] < a[right])
			return left;
		else if (a[mid] > a[right])
			return mid;
		else
			return right;
	}
}

3、挖坑法

（1）选择第一元素作为基准值，并且作为坑
（2）先从右边（下标设为end）开始寻找小于基准值的元素，找到后将该元素填入坑（pivot ）中，然后该元素原来的位置成为新的坑，再从左边（下标设为begin）寻找大于基准值的元素，找到后将该元素填入坑中，然后该元素原来的位置成为新的坑，这样一直下去，直到end和begin相遇结束
（3）我们再对数组重新划分区间（以坑（pivot ）的位置来划分左右区间，坑的元素不动），再进行上述过程，直到不能划分就结束（这里用递归实现）
如：
这是第一次划分的过程：

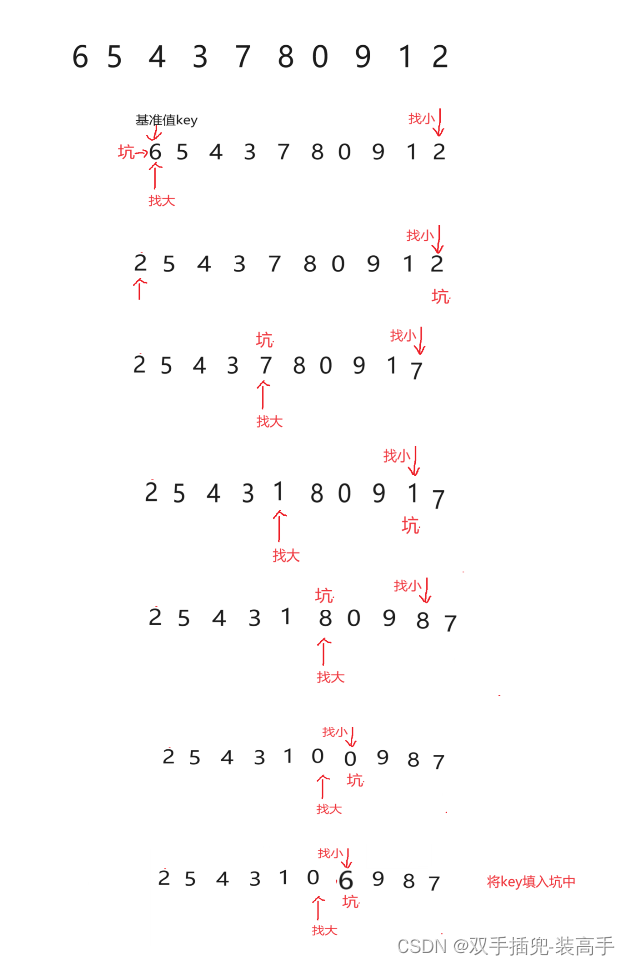
对右边进行第二次过程：

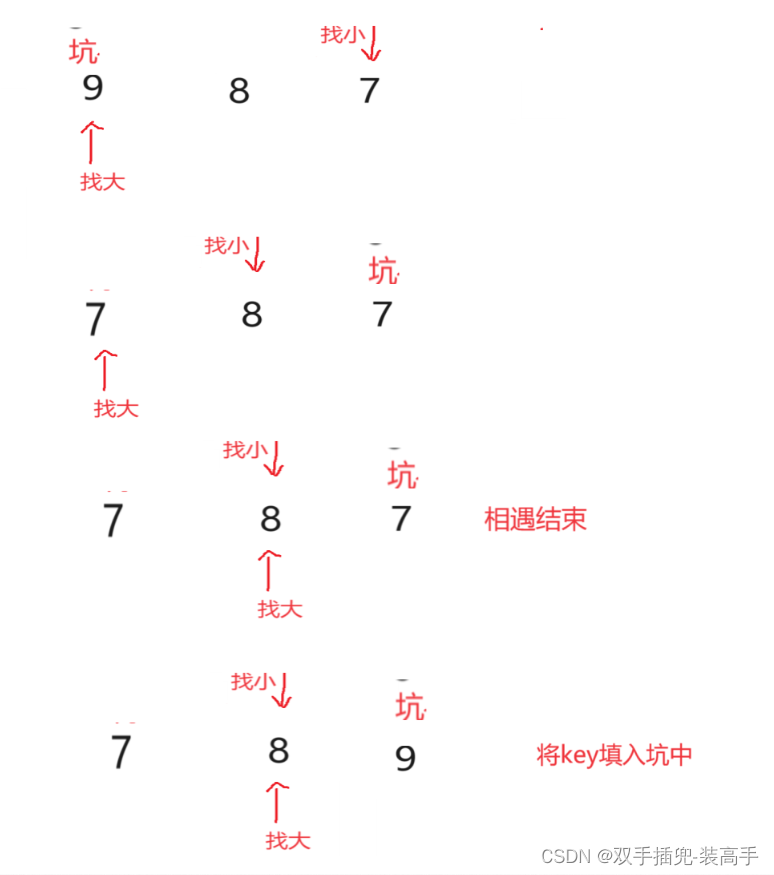
往下以此类推
代码实现：

//打印
void Print(int* arr, int n) {

	for (int i = 0; i < n; i++)
		printf("%d ", arr[i]);
}
//三数取中
int GetMidIndex(int* a, int left, int right) {
	int mid = (left + right) >> 1;
	if (a[mid] > a[left]) 
	{
		if (a[right] > a[mid])
			return mid;
		else if (a[right] > a[left])
			return right;
		else
			return left;
	}
	else 
	{
		if (a[left] < a[right])
			return left;
		else if (a[mid] > a[right])
			return mid;
		else
			return right;
	}
}


//挖坑法
int PartSort1(int* a, int left, int right) {
int	 index= GetMidIndex(a, left, right);//三数取中
        Swap(&a[left], &a[index]);//我们始终都选择第一个位置作为基准值，求出中间值与第一个位置的值交换
		int begin = left;//左边位置
		int end = right;//右边位置
		int key = a[begin];//基准值
		int pivot = begin;//坑
		//过程：
		while (begin < end)
		{    //找小
			while (a[end] >= key && end > begin)
				end--;
			a[pivot] = a[end];
			pivot = end;
			//找大
			while (a[begin] <= key && end > begin)
				begin++;
			a[pivot] = a[begin];
			pivot = begin;;
		}
		//最后将key填回坑中
		a[pivot] = key;
		return pivot;//返回坑的位置
}
void QuickSort(int* a, int left, int right)
{
	//递归结束条件
	if (left >= right)
		return;
		//过程，并返回新坑的位置，按照坑的位置，重新划分区间
	int keyIndex=  PartSort1(a, left, right);
	//进行递归
	QuickSort(a, left, keyIndex - 1);
	QuickSort(a, keyIndex + 1, right);
}
int main() {
	int a[] = { 6,7,2,9,5,1,3,0,4,8 };
	Print(a, sizeof(a) / sizeof(a[0]));
	QuickSort(a, 0, sizeof(a) / sizeof(a[0]) - 1);
		printf("\n");
	Print(a, sizeof(a) / sizeof(a[0]));
	return 0;
}

运行结果：

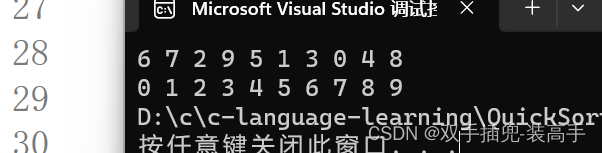
4、左右指针法

左右指针法是挖坑法的一个变形
（1）还是以第一个元素作为基准值，然后从右边（下标设为end）开始，找到一个比基准值小的元素，再从左边（下标设为begin）找到一个比基准值大的数，然后将这两个元素交换，这样大的就放到了右边，小的就放到了左边。
（2）一直找到begin>=end结束，最后将begin位置的元素和基准值一交换，这样就完成了
如：
第一趟过程：

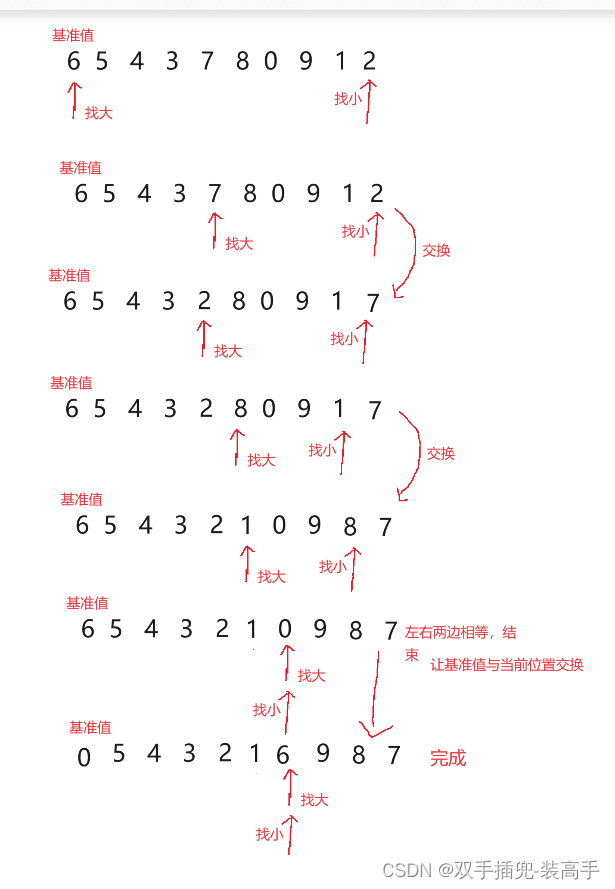
代码实现：

//左右指针
int PartSort2(int* a, int left, int right) {
//三数取中
	int	 index = GetMidIndex(a, left, right);
	Swap(&a[left], &a[index]);
	int begin = left;//左
	int end = right;//右
	int keyi = begin;//基准值
	while (begin < end)
	{    //找小a[keyi]直到找到小的
		while (a[end] >= a[keyi] && end > begin)
			end--;
		//找大 直到找到大的
		while (a[begin] <= a[keyi] && end > begin)
			begin++;
			//发生交换
		Swap(&a[end], &a[begin]);
	}
	//最后数组中的基准值和比基准值小的元素交换（这个位置就是相遇的位置）
	Swap(&a[keyi], &a[begin]);
	return begin;
}
void QuickSort(int* a, int left, int right)
{
	//递归结束条件
	if (left >= right)
		return;
	int keyIndex=  PartSort2(a, left, right);
	QuickSort(a, left, keyIndex - 1);//递归
	QuickSort(a, keyIndex + 1, right);
}

5、前后指针法

（1）还是以第一个元素当作基准值，设置一个前指针（begin）和后指针（end），后指针往后走，遇到一个比基准值小的数就让前指针往前走一步且begin！=end两元素交换，之后end继续往后走，再找小的元素
（2）直到end>数组长度-1就结束。然后让基准值与begin位置的值交换，就完成了
如：
第一趟过程：

代码实现：

//前后指针
int PartSort3(int* a, int left, int right) {
//三数取中
	int	 index = GetMidIndex(a, left, right);
	Swap(&a[left], &a[index]);
	int begin = left;//前指针
	int end = left + 1;//后指针
	int keyi = begin;//基准值
	while (end <= right)//end小于数组长度-1
	{   
		while (a[end] < a[keyi] && ++begin!=end)//找到并且前后指针不相等，进行交换
			Swap(&a[end], &a[begin]);
		end++;//找不找的到都要往前走
	}
	Swap(&a[keyi], &a[begin]);//最后基准值与最后一个小于基准值的元素交换
	return begin;
}
void QuickSort(int* a, int left, int right)
{
	//递归结束条件
	if (left >= right)
		return;
	int keyIndex=  PartSort3(a, left, right);
	QuickSort(a, left, keyIndex - 1);//递归
	QuickSort(a, keyIndex + 1, right);
}

6、非递归实现快速排序

递归的缺陷：栈帧深度太深，栈空间不够用，可能会溢出
递归改非递归：1、直接改循环(简单) 2、借助数据结构栈模拟递归过程(复杂一点)

我们这里直接改循环很难改，所以是借助数据结构栈来模拟实现的，不会栈的可以看看这个：http://t.csdnimg.cn/7JttS
我们将开始的区间（0，size-1（数组长度-1））进行压栈，先压size-1，因为栈是后进先出的，之后就是取出栈中的元素（一个区间）再利用上面三种方法中的一种对数组进行划分，再利用返回值进行再次划分，如果返回值不在（0，size-1）范围内就不进行压栈，如果在就进行压栈，当栈清空了，就说明排好序了，此时结束。
实现的过程是和上面一样的。
代码实现：
栈：
Stack.h

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include<stdbool.h> 

typedef int STDataType;

typedef struct Stack
{
	STDataType* a;
	int top;
	int capacity;
}ST;

void StackInit(ST* ps);//初始化
void StackDestory(ST* ps);//释放
// 入栈
void StackPush(ST* ps, STDataType x);
// 出栈
void StackPop(ST* ps);
STDataType StackTop(ST* ps);//出栈的元素

int StackSize(ST* ps);//返回元素个数
bool StackEmpty(ST* ps);//是否为空

Stack.c

#include"Stack.h"
void StackInit(ST* ps)//初始化
{
	assert(ps);
	ps->a = (STDataType*)malloc(sizeof(STDataType)*4);
	ps->capacity = 4;
	ps->top = 0;
}
void StackPush(ST* ps, STDataType x) //入栈
{
	assert(ps);
	if (ps->capacity == ps->top) {
		STDataType* p = (STDataType*)realloc(ps->a,sizeof(STDataType) * ps->capacity*2);
		if (p == NULL) {
			printf("reallocfail\n");
			exit(-1);//终止程序
		}
		else {
			ps->a =p;
			ps->capacity = ps->capacity * 2;
		}
	}
	ps->a[ps->top] = x;
	ps->top++;
}

void StackPop(ST* ps) {// 出栈
	assert(ps);
	assert(ps->top);
	ps->a[ps->top - 1] = 0;
	ps->top--;
}
STDataType StackTop(ST* ps) {//出栈的元素
	assert(ps);
	assert(ps->top);
	return ps->a[ps->top - 1];
}
int StackSize(ST* ps) {//数组元素个数
	assert(ps);
	return ps->top;
}
bool StackEmpty(ST* ps) {//判断是否为空
	assert(ps);
	return ps->top==0;
}
void StackDestory(ST* ps) {//释放
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->top = 0;
	ps->capacity = 0;
}

快速排序：

//交换
void Swap(int* a, int* b) {
	int t = *a;
	*a = *b;
	*b = t;
}
//打印
void Print(int* arr, int n) {

	for (int i = 0; i < n; i++)
		printf("%d ", arr[i]);
}
//三数取中
int GetMidIndex(int* a, int left, int right) {
	int mid = (left + right) >> 1;
	if (a[mid] > a[left]) 
	{
		if (a[right] > a[mid])
			return mid;
		else if (a[right] > a[left])
			return right;
		else
			return left;
	}
	else 
	{
		if (a[left] < a[right])
			return left;
		else if (a[mid] > a[right])
			return mid;
		else
			return right;
	}
}

//挖坑法
int PartSort1(int* a, int left, int right) {
int	 index= GetMidIndex(a, left, right);
        Swap(&a[left], &a[index]);
		int begin = left;
		int end = right;
		int key = a[begin];
		int pivot = begin;
		while (begin < end)
		{    //找小
			while (a[end] >= key && end > begin)
				end--;
			a[pivot] = a[end];
			pivot = end;
			//找大
			while (a[begin] <= key && end > begin)
				begin++;
			a[pivot] = a[begin];
			pivot = begin;;
		}
		a[pivot] = key;
		return pivot;



//用栈模拟非递归
void QuickSortNonR(int* a, int n) {
	ST s;
	StackInit(&s);//初始化
	StackPush(&s, n - 1);//压栈
	StackPush(&s, 0);//压栈
	while (!StackEmpty(&s)) {//判断栈是否为空
		int left = StackTop(&s);//取元素
		StackPop(&s);//出栈
		int right= StackTop(&s);
		StackPop(&s);
	int keyIndex =PartSort1(a, left, right);//调用挖坑//划分
	if (keyIndex + 1 < right)//判断是否入栈
	{
		StackPush(&s, right);
		StackPush(&s, keyIndex + 1);
	}
	if (keyIndex - 1 > left) {//判断是否入栈
		StackPush(&s, keyIndex - 1);
		StackPush(&s, left);
	}
	}
	StackDestory(&s);//释放
}
int main() {
	int a[] = { 6,7,2,9,5,1,3,0,4,8 };
	Print(a, sizeof(a) / sizeof(a[0]));
		printf("\n");
	Print(a, sizeof(a) / sizeof(a[0]));
	return 0;
}

7、时间复杂度

我们用挖坑法来算一下

这里按实际来算的话就是，走end+begin就是n次，所以这里时间O（N）；

递归次数：
每次减半，就是N/2/2/2/2…，所以N=logN（以2为底），所以O（logN）

所以时间复杂度为：O（N*logN）；

8、稳定性

概念：

假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[4]，且r[1]在r[4]之前，而在排序后的序列中，r[1]仍在r[4]之前，则称这种排序算法是稳定的;否则称为不稳定的。

快速排序不稳定
如：

以上就是我的分享了，如果有什么错误，欢迎在评论区留言。
最后，谢谢大家的观看！