数据结构与算法:基于比较的排序算法:选择、冒泡、插入、归并的动图演示和java代码,排序时间复杂度、空间复杂度、稳定性总结表格
选择排序
选择排序是先在0~N-1上选择一个最小值排到最前面,然后再在1到N-1上选一个次小的,以此类推。

public static selectionSort(int[] arr){
if(arr==null||arr.length<2){
return;
}
//每次从i n-1 选一个最小的放前面
for(int i=0;i<=arr.length-2;i++){
int minIdx = i;
for(int j=i+1;j<=arr.length-1;j++){
if(arr[minIdx]>arr[j]) minIdx=j;
}
swap(arr,i,minIdx);
}
}
public static void swap(int[] arr,int i,int j){
if(i==j) return;
arr[i]=arr[i]^arr[j];
arr[j]=arr[i]^arr[j];
arr[i]=arr[i]^arr[j];
}
冒泡排序

public static selectionSort(int[] arr){
if(arr==null||arr.length<2){
return;
}
//每次遍历0 i
for(int i=arr.length-1;i>=1;i--){
for(int j=0;j<i;j++){
if(arr[j+1]>arr[j]) swap(arr,j,j+1);
}
}
}
public static void swap(int[] arr,int i,int j){
if(i==j) return;
arr[i]=arr[i]^arr[j];
arr[j]=arr[i]^arr[j];
arr[i]=arr[i]^arr[j];
}
插入排序
插入排序是先让0到1变得有序,然后让0到2变得有序,以此类推。

public static void insertionSort(int[] arr){
if(arr==null||arr.length<2){
return;
}
//0~0 已经有序
//0~i 想变有序
for(int i=1;i<arr.length;i++){
for(int j=i-1;j>=0&&arr[j]>arr[j+1];j--){
swap(arr,j,j+1);
}
}
}
public static void swap(int[] arr, int i, int j){
if(i==j) return;
arr[i]=arr[i]^arr[j];
arr[j]=arr[i]^arr[j];
arr[i]=arr[i]^arr[j];
}
归并排序

public static void mergeSort(int[] arr){
process(arr,0,arr.length-1);
}
public static void process(int[] arr,int L,int R){
if(L==R) return;
int mid=L+(R-L)>>1;
process(arr,L,mid);
process(arr,mid+1,R);
merge(arr,L,mid,R);
}
public static void merge(int[] arr,int L,int mid,int R){
int[] temp=new int[R-L+1];
int i=0;
int p1=L;
int p2=R;
while(p1<=mid&&p2<=R){
if(arr[p1]<arr[p2]) temp[i++]=arr[p1++];
else temp[i++]=arr[p2++];
}
while(p1<=mid) temp[i++]=arr[p1++];
while(p2<=R) temp[i++]=arr[p2++];
for(i=0;i<temp.length;i++){
arr[L+i]=temp[i++];
}
}
时间复杂度,用Master主定理算出来是O(N*logN),空间复杂度为O(N)
稳定性
定义
一个排序算法具有稳定性的意思是在排序相同值数据的前后,数据之间的相对顺序不变。
譬如我现在有一个待排序列:3 3 1
那么前两个3是值相等的,我们现在给这个待排序列打上标记:3① 3② 1
排完序后这个序列依旧是3①在3②的左边,那么我们就称这个排序算法具有稳定性。
应用场景
要求稳定性的场景一般是多条件排序,我们需要保留前几轮排序的相对顺序。
譬如一个商品排行榜的比较标准为:质量分高的在前,质量分相同的话看价格,价格低对的在前。这时候我们就需要具有稳定性的算法,因为相当于有两轮条件比较,质量分和价格。我们在比较价格时需要保证质量分排序的相对顺序不变。
体现在数据结构中就是,一般自定义的,复杂的数据结构才需要稳定性的存在。
基于比较的排序对比总结
目前在基于比较的排序算法中,没有找到时间复杂度为O(N*logN) ,空间复杂度为O(1),又稳定的排序。
面试版
以下稳定性为√的意思是该算法可以实现成稳定性的,要看具体的实现逻辑。
但是为×的就是一般情况下该算法是无法实现成稳定性的(但如果)。
且快排是基于随机数实现的快排。
| 算法 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| 选择 | O(N^2) | O(1) | × |
| 冒泡 | O(N^2) | O(1) | √ |
| 插入 | O(N^2) | O(1) | √ |
| 归并 | O(N*logN) | O(N) | √ |
| 快排 | O(N*logN) | O(logN) | × |
| 堆 | O(N*logN) | O(1) | × |
各个排序算法关于稳定性的细节
一般只要是跨多个值交换位置的算法,就会丧失稳定性。
选择排序
选择排序是先在0~N-1上选择一个最小值排到最前面,然后再在1到N-1上选一个次小的,以此类推。
这种跨多个值交换位置的,很明显没有稳定性。譬如序列:3① 3② 1 3③
最终会变为:1 3② 3① 3③
冒泡排序
因为是相邻位置交换,所以具有稳定性
插入排序
插入排序是先让0到1变得有序,然后让0到2变得有序,以此类推。
那么我们只需要在遍历当前数并往前比较时,碰到一样的不交换,即可保证稳定性。
归并排序
归并排序是先让小区间变得有序,然后合并成大区间。
我们只需要在合并时,左右区间是相等的数,先取左那么就可保证稳定性。
快速排序
快速排序的两个版本,第一个版本是,通过选择一个基准值,将数组分割成两个区,一个区小于等于基准值,一个区大于基准值。然后递归地对两区进行快速排序。
第二个版本是,通过选择一个基准值,将数组分割成三个区,一个区小于基准值,一个区等于基准值,一个区大于基准值。然后递归地对三区进行快速排序。
如果是第一个版本,当遍历到小于等于基准值的数时,就要和小于等于区的下一个数做交换。这一般也是跨多个值进行交换的,所以没有稳定性。
如果是第二个版本,当遍历到小于基准值的数时,就要和小于区的下一个数做交换。这一般也是跨多个值进行交换的,所以没有稳定性。
堆排序
堆排序更不用说,从始至终所有步骤都不能保证稳定性。
详细版
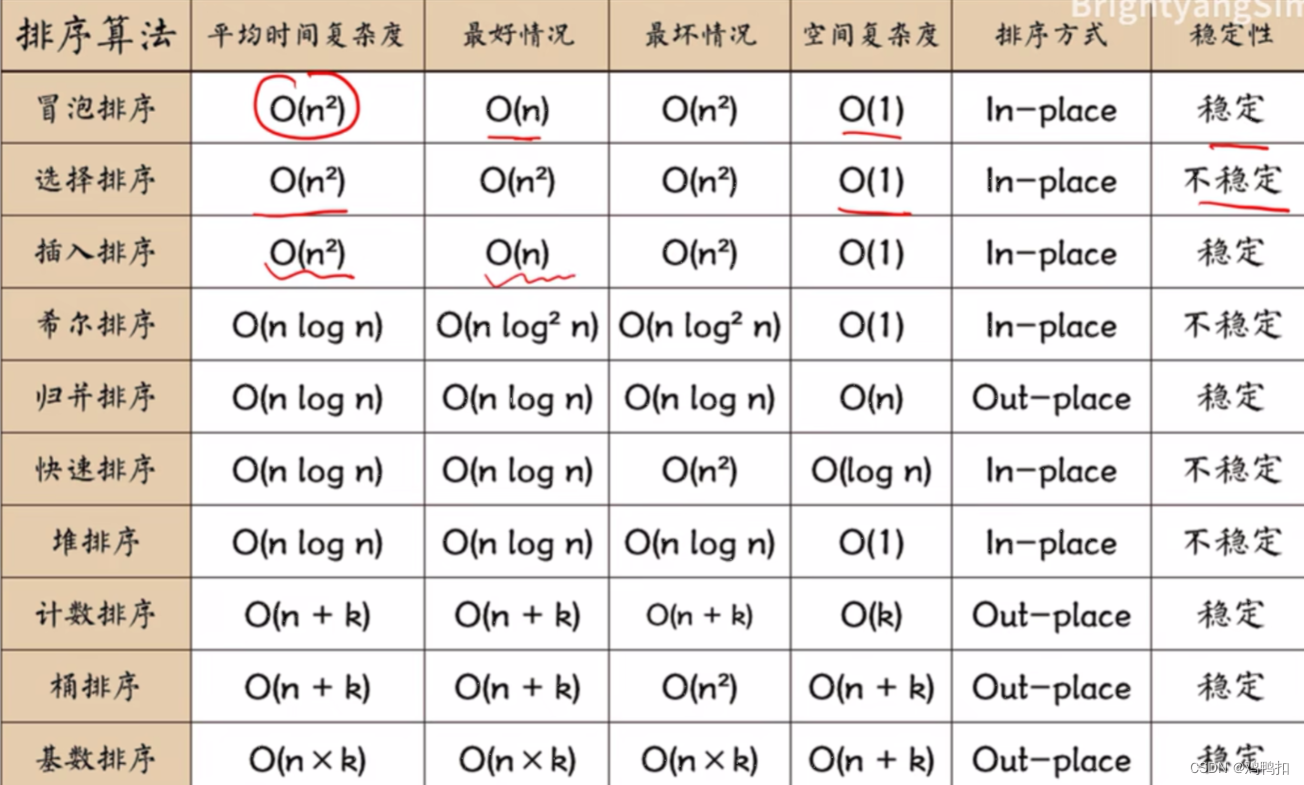
排序算法的优化
归并算法可以利用内部缓存法将空间复杂度优化为O(1),但是代码实现过于复杂,不建议掌握。
同时“原地归并排序”也可以将空间复杂度优化为O(1),但是时间复杂度就变为O(N^2)了。
快速排序可以实现稳定性,但是代码实现过于复杂,不建议掌握。
总而言之,不用去考虑太多这些主流版本之外的优化版本。
工程上对于排序算法的改进
在项目或者工程中一般会考虑以下两点:1、样本量小和大。2、是否需要稳定性
譬如样本量小时,时间复杂度上O(N^2)和O(N*logN)区别不大,但O(N平方)算法的空间复杂度几乎都为O(1),所以小样本其实应该用选择排序、冒泡排序、插入排序等算法。
同时,
本篇文章看不懂的可以去看视频,因为本篇文章是基于此视频做的总结和扩充笔记:https://www.bilibili.com/video/BV13g41157hK?p=6
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!