立体视觉几何 (二)
1.视差

2.立体匹配
-
立体匹配的基本概念:
- 匹配目标: 在立体匹配中,主要目标是确定左图像中像素的右图像中的对应像素。这个对应像素通常位于相同的行。
- 视差(Disparity): 视差
d是右图像中对应像素xr和左图像中像素xl之间的水平位置差。视差是深度信息的关键指标。
-
匹配方法:
- 方法涉及在左图像中以某个像素为中心取一个窗口
W,然后将这个窗口沿水平方向平移视差d,并将其放置在右图像中。 - 接着比较左图像中窗口
W和右图像中平移后窗口W内的像素强度值。
- 方法涉及在左图像中以某个像素为中心取一个窗口
-
比较度量:
-
比较度量公式通常有如下形式:
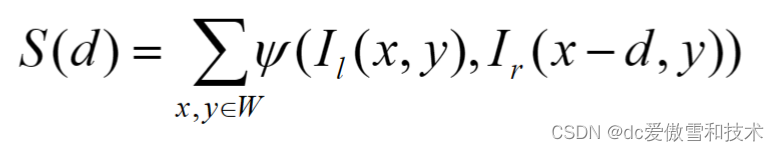
-
这里
S(d)是某个特定视差d的匹配得分。 -
I_l(x, y)和I_r(x+d, y)分别是左图像和右图像中相应位置的像素强度值。 -
求和是对窗口
W中所有像素进行的,意味着比较的是整个窗口的像素强度差的总和或平均值。
-
-
分析:
- 这种方法基于的假设是,左图像中的窗口和右图像中相对应的窗口在视觉内容上应该是相似的。
- 通过调整视差
d并计算每个可能的d值的匹配得分S(d),可以确定最佳匹配视差,即得分最低(或最高,取决于具体实现)的那个d。 - 这种方法有效但计算量较大,尤其是在处理大尺寸图像和大窗口时。
总的来说,这个立体匹配方法是通过比较左图像中的一个窗口和右图像中相应平移的窗口来寻找最佳匹配视差的一种经典方法。它在众多应用中被广泛使用,如3D重建、机器人导航等。
匹配函数
在立体视觉中,为了找到两个图像间的对应像素,通常会使用不同的匹配函数来计算像素间的相似度。您提到的两种匹配函数,SSD(平方差之和)和SAD(绝对差之和),都是用来衡量两幅图像中对应窗口内像素差异的常见方法。让我们详细分析这两种函数:
1. SSD(Sum of Squared Differences)
-
定义:
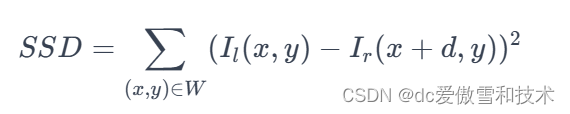
其中 (I_l) 和 (I_r) 分别是左图像和右图像中的像素强度,(d) 是视差,(W) 是选定的窗口。
-
特点:
- SSD通过对像素差的平方求和,对大的像素差异给予更大的权重。
- 在图像较为清晰、噪声较低的情况下,SSD能够有效地突出实际的像素差异。
-
缺点:
- 当图像含有噪声时,SSD会由于平方项的作用,过分放大噪声的影响,导致匹配误差增大。
2. SAD(Sum of Absolute Differences)
-
定义:
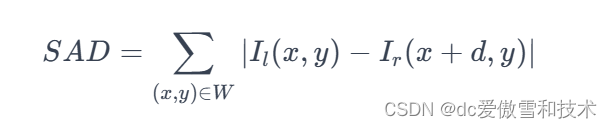
同样地,这里 (I_l) 和 (I_r) 是左右图像中的像素强度,(d) 是视差,(W) 是窗口。
-
特点:
- SAD计算的是像素差的绝对值之和,对所有像素差异给予平等的权重。
- 相比SSD,SAD对噪声的敏感性较低,因此在噪声较多的图像中表现更好。
-
缺点:
- SAD可能不如SSD敏感于大的像素差异,有时可能忽略重要的特征差异。
总结
- SSD和SAD都是衡量图像间相似度的有效方法,但它们各有优势和局限性。
- SSD更适用于低噪声图像,能够强调大的像素差异,但在噪声较多的情况下可能不理想。
- SAD在处理噪声图像时表现更好,但可能对某些重要的像素变化不够敏感。
- 选择哪种匹配函数取决于具体的应用场景和图像特性,以及处理速度的要求。在某些硬件架构上,SAD的计算可能比SSD更快。
您提到了相关性(Correlation)和归一化相关性(Normalized Correlation)这两种用于立体匹配的方法。让我们分析这两种方法的定义、特点和应用场景。
3. 相关性(Correlation)
-
定义:
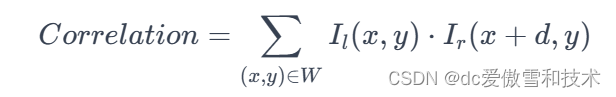
这里的 (I_l) 和 (I_r) 分别表示左右图像中的像素强度,(d) 是视差,(W) 是考虑的窗口。
-
特点:
- 相关性衡量的是两个图像窗口中对应像素强度的乘积之和。
- 当两个图像窗口完全相同时,相关性达到最大值。
- 相关性在某种程度上与SSD相似,但更直接地考虑了像素强度的乘积。
-
应用:
- 相关性适用于像素强度直接相关的情况,但通常需要与归一化方法结合使用,以提高其鲁棒性。
4. 归一化相关性(Normalized Correlation)
-
定义:
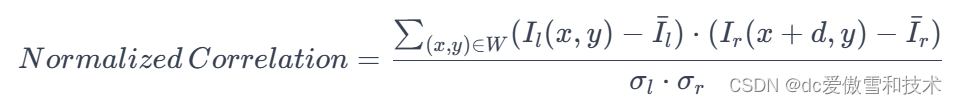
其中 (\bar{I}_l) 和 (\bar{I}_r) 分别是左右图像窗口的平均像素强度,(\sigma_l) 和 (\sigma_r) 是左右图像窗口的标准差。
-
特点:
- 归一化相关性考虑了图像窗口的像素强度分布,消除了绝对强度的影响。
- 它的值总是在 -1 到 +1 之间,+1 表示完美匹配。
- 相比未归一化的相关性,归一化相关性在不同光照和对比度条件下更加稳定。
-
应用:
- 归一化相关性计算更加复杂和耗时,但它适用于需要高鲁棒性和精确度的场景。
- 特别适用于图像对比度和亮度变化较大的情况。
总结
- 相关性和归一化相关性都是衡量两个图像窗口相似度的有效方法。
- 相关性简单但受光照和对比度影响较大,而归一化相关性虽然计算更复杂,但在处理不同光照和对比度条件下的图像时更加稳定和准确。
- 根据具体的应用需求和图像条件,可以选择最适合的方法。

-
视差的定义:
- 视差是指在双目立体视觉系统中,同一个三维点在左右两个摄像机成像平面上投影点之间的水平距离差。
- 在一对校正后的双目图像中,视差通常表现为同一物体或场景点在两幅图像中的水平位置差。
-
视差与深度的关系:
- 在立体视觉中,视差与场景中物体到摄像机的距离(即深度)成反比关系。这意味着物体离摄像机越近,其在两个摄像机成像平面上的投影点的视差就越大。
- 反之,如果物体离摄像机很远,其投影点的视差就会很小,甚至接近于零。在极端情况下,无限远处的物体(例如远处的星星)在两个摄像机中的视差几乎为零。
-
视差的应用:
- 在计算机视觉和机器人领域,视差图(一幅图像,其中每个像素的值代表该像素的视差)被用来估计场景的三维结构。
- 通过计算和分析视差图,可以确定物体的大致位置和形状,这对于三维重建、机器人导航、避障系统等应用至关重要。
-
视差的计算:
- 视差的计算通常涉及在一对双目图像中为每个像素点寻找最佳的匹配点,并计算这两点之间的水平位置差。
- 这个过程可以通过各种算法实现,如区块匹配、半全局匹配(SGM)等。
总结
“视差是深度的倒数”这一概念是立体视觉领域的基础,它表明物体到摄像机的距离越近,其在双目图像中的视差就越大。这个原理在多个领域有着广泛的应用,特别是在需要精确深度信息的场景中。通过分析视差,可以获取有关场景和物体的三维信息,这对于许多计算机视觉应用至关重要。
匹配算法实现

这个算法的目标是在一对双目图像中为每个像素找到最佳匹配视差。让我们逐步分析这个算法的实现和关键点:
算法概述
-
外部循环 - 遍历每个像素:
- 算法首先通过两个嵌套循环遍历图像中的每个像素(坐标为
(x, y))。 xsize和ysize分别是图像的宽度和高度。
- 算法首先通过两个嵌套循环遍历图像中的每个像素(坐标为
-
视差范围:
- 第三个循环遍历所有可能的视差值
d,从dmin到dmax。这个范围定义了算法搜索匹配的深度。
- 第三个循环遍历所有可能的视差值
-
初始化最佳匹配分数:
- 对于每个像素,初始化一个最佳匹配分数
Sbest为最大值(可能表示无穷大或一个足够大的数)。
- 对于每个像素,初始化一个最佳匹配分数
-
局部窗口 - 计算匹配分数:
- 对于每个视差值
d,在像素(x, y)周围的一个小窗口内(大小由w定义)计算匹配分数S(d)。 S(d)是窗口内所有像素的某种匹配度量(例如 SSD 或 SAD)的累积。
- 对于每个视差值
-
更新最佳匹配和视差:
- 如果当前的匹配分数
S(d)小于当前的最佳分数Sbest,则更新Sbest为S(d),并记录下这个视差值d作为当前像素的最佳视差dbest(x, y)。
- 如果当前的匹配分数
算法的优化
-
循环顺序可调换:
- 算法中的循环(x, y, d)可以按不同的顺序执行。不同的顺序可能影响算法的效率。
-
计算优化:
- 尽管这个算法看起来计算量巨大,但通过重用部分结果可以有效地提高效率。例如,当计算邻近像素的匹配分数时,可以重用上一个像素计算的部分结果。
- 还可以使用积分图(Integral Image)等技术来优化窗口内的匹配度量计算。
总结
这个算法是一个典型的窗口基础的双目匹配算法。它适用于计算每个像素点的最佳匹配视差,进而可以用来构建整个视差图。虽然基本的实现看起来计算量巨大,但通过各种优化技术,可以在实际应用中高效地执行。这种类型的算法是计算机视觉和机器人领域中三维重建和深度感知的基础。
import numpy as np
def stereo_matching(left_img, right_img, dmin, dmax, window_size):
xsize, ysize = left_img.shape
w = window_size // 2
dbest = np.zeros_like(left_img, dtype=np.float32)
for x in range(w, xsize - w):
for y in range(w, ysize - w):
Sbest = float('inf')
for d in range(dmin, dmax + 1):
if x + d + w >= xsize: # 确保窗口不会超出图像范围
continue
# 计算匹配分数,这里以SAD为例
Sd = 0
for u in range(-w, w + 1):
for v in range(-w, w + 1):
diff = int(left_img[x + u, y + v]) - int(right_img[x + u + d, y + v])
Sd += abs(diff)
# 更新最佳匹配和视差
if Sd < Sbest:
Sbest = Sd
dbest[x, y] = d
return dbest
# 示例使用
# left_img 和 right_img 需要是加载的左右图像
# dmin 和 dmax 分别是视差搜索的最小值和最大值
# window_size 是匹配窗口的大小,通常是一个奇数,例如5或9
# disparity_map = stereo_matching(left_img, right_img, dmin, dmax, window_size)
函数功能
- 函数定义:
stereo_matching(left_img, right_img, dmin, dmax, window_size)是一个双目匹配函数,它接收左右两个图像、最小和最大视差值以及匹配窗口的大小作为输入。
主要步骤
-
初始化:
- 获取输入图像的尺寸
xsize, ysize。 - 定义一个与左图像同样大小的数组
dbest来存储每个像素的最佳视差值。
- 获取输入图像的尺寸
-
像素遍历:
- 通过两层嵌套循环遍历图像中的每个像素。循环从
w(窗口半径)开始,以避免窗口超出图像边界。
- 通过两层嵌套循环遍历图像中的每个像素。循环从
-
视差计算:
- 对于每个像素,内部循环遍历所有可能的视差值
d。 - 判断条件
if x + d + w >= xsize用于确保窗口在进行视差计算时不会超出图像的右侧边界。
- 对于每个像素,内部循环遍历所有可能的视差值
-
匹配分数(SAD)计算:
- 使用SAD(绝对差之和)方法来计算匹配分数
Sd。这是通过比较左图像窗口和右图像相应窗口(考虑视差d)中的像素强度来完成的。
- 使用SAD(绝对差之和)方法来计算匹配分数
-
更新最佳匹配视差:
- 如果当前视差的匹配分数
Sd小于之前的最佳分数Sbest,则更新Sbest并记录当前的视差d作为该像素的最佳视差dbest[x, y]。
- 如果当前视差的匹配分数
使用示例
- 要使用这个函数,你需要提供左右图像(
left_img和right_img),视差搜索范围(dmin和dmax)以及匹配窗口的大小(window_size)。窗口大小通常是一个奇数,例如5或9。 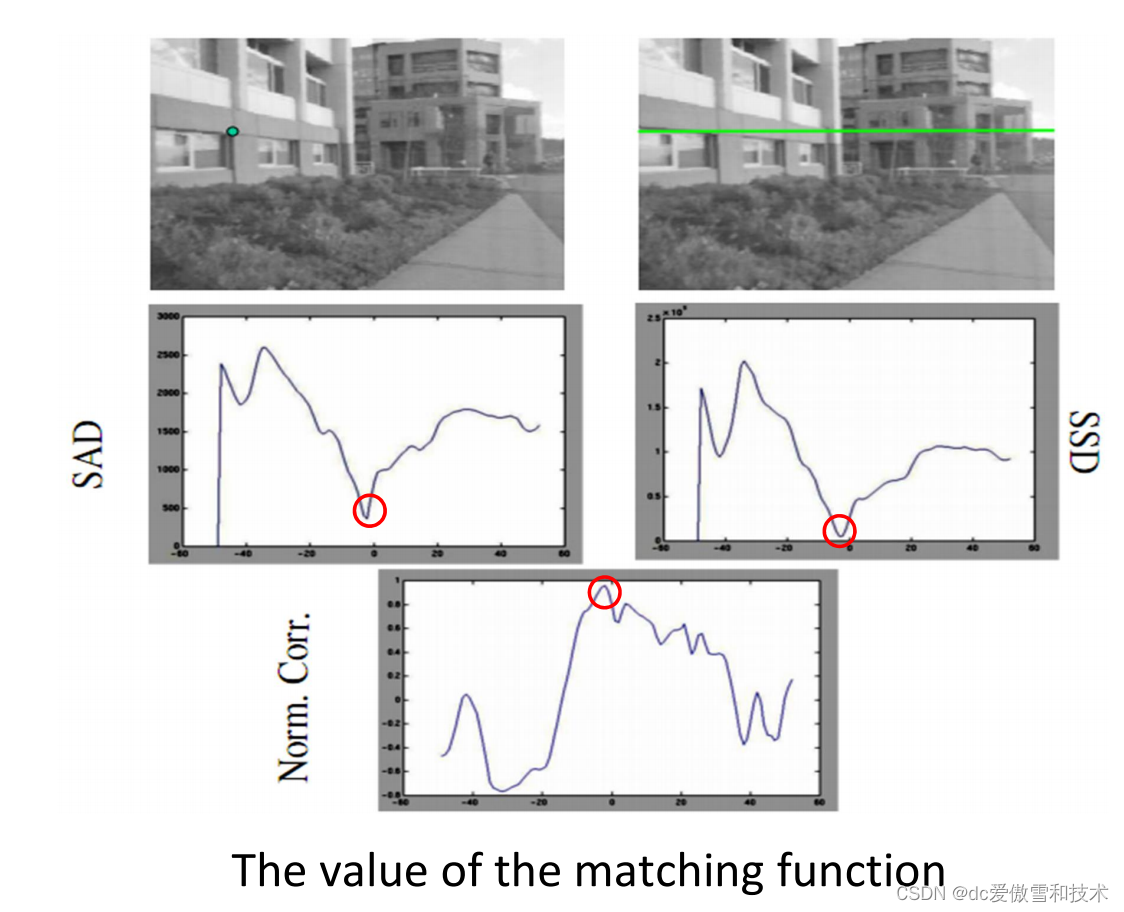
3.恢复场景点的3D坐标
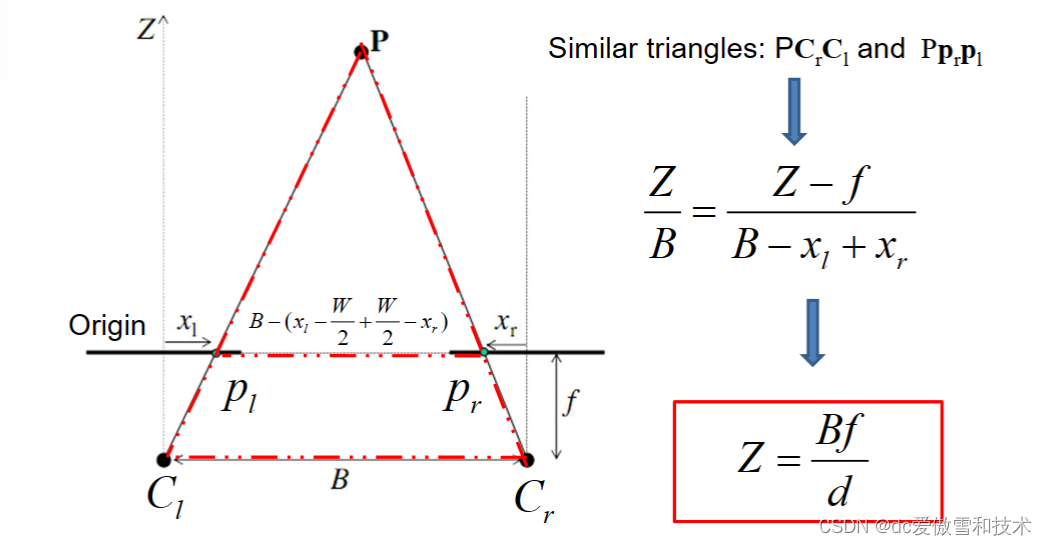
假设两个相机具有平行的像平面
f - 相机的焦距
B - 光心之间的距离
一些重要的结论
“这个关系是立体视觉的基本关系。” - 这个陈述表明在立体视觉中有一个基本关系,对于理解和处理立体图像非常重要。
“深度与视差成反比。” - 这个陈述指出,在立体视觉中,深度(物体到相机的距离)与视差(左右两个相机观察到的物体位置的差异)成反比关系。换句话说,随着视差减小,深度增加。
“一旦我们知道Z,其他两个坐标可以使用标准透视方程推导出来。” - 这表明在立体视觉系统中,如果您知道物体的深度(Z),您可以使用标准透视方程计算出其其他两个坐标(X和Y)。这是计算机视觉和三维重建中的常见概念。
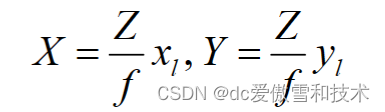
“相机校准:内参和外参参数。” - 这提到了相机校准的重要性,包括确定相机的内参参数(例如焦距、光学中心)和外参参数(例如相机位置和方向)。校准对于在立体视觉中准确估计深度和进行三维重建非常重要。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- vue列表飞入效果
- 揭秘亚马逊:如何通过API轻松获取全球商品详细信息
- 【什么是反射机制?为什么反射慢?】
- 大尺寸产品外径难实时测量?请看大直径测径仪系列!
- 亚马逊云科技AI应用 SageMaker 新突破,机器学习优势显著
- 探索商超货架场景目标检测性能,基于YOLOv8【n/s/m/l/x】全系列参数模型开发构建商超货架场景下亨氏米粉食品种类检测识别系统
- 二叉树知识总结
- 答题小程序源码系统:自带流量主广告位+视频激励广告 带完整的代码安装包以及搭建教程
- 【前端面试题】每日一个前端面试专题
- 飞天使-k8s知识点8-kubernetes资源对象-编写中