代码随想录算法训练营第三十九天|62.不同路径、63. 不同路径 II
发布时间:2024年01月21日
题目:62.不同路径
文章链接:代码随想录
视频链接:LeetCode:62.不同路径
题目链接:力扣题目链接
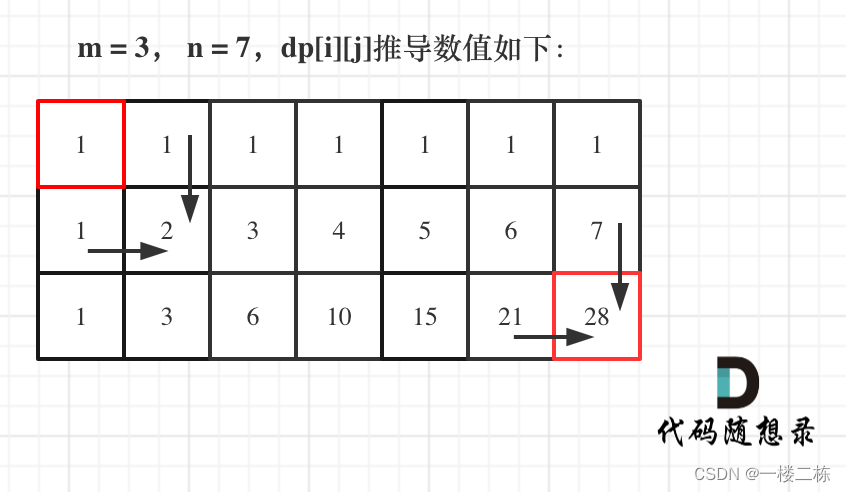
图释:
class Solution {
public:
// 确定dp数组(dp table)以及下标的含义 dp[m][n], dp[i][j]表示[i][j]位置有几种路径(而不是有多少步)
// 确定递推公式 dp[i][j]=dp[i-1][j]+dp[i][j-1]
// dp数组如何初始化 因为只能向右和向下移动,所以第一行和第一列都只有一条路径 dp[0][j]=1, dp[i][0]=1
// 确定遍历顺序 从左往右,从上往下
// 举例推导dp数组
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m,vector<int>(n, 0)); //m行n列的二位数组vector
// 初始化
for(int i=0; i<m; i++) dp[i][0]=1; // 第一列
for(int j=0; j<n; j++) dp[0][j]=1; // 第一行
for(int i=1; i<m; i++){
for(int j=1; j<n; j++){
dp[i][j]= dp[i-1][j]+dp[i][j-1];
}
}
return dp[m-1][n-1];
}
};题目:63. 不同路径 II
文章链接:代码随想录
视频链接:LeetCode:63.不同路径||
题目链接:力扣题目链接
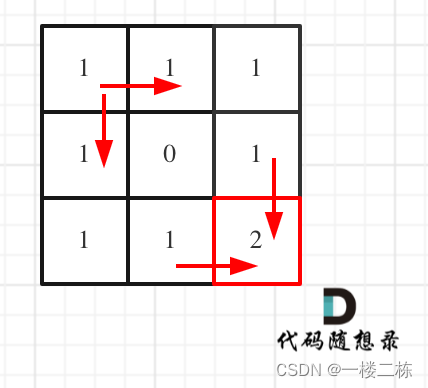
图释:
class Solution {
public:
// 确定dp数组(dp table)以及下标的含义 dp[m][n], dp[i][j]表示[i][j]位置有几种路径(而不是有多少步)
// 确定递推公式 dp[i][j]=dp[i-1][j]+dp[i][j-1] 当该格子为障碍的时候,路径为0
// dp数组如何初始化 因为只能向右和向下移动,所以第一行和第一列都只有一条路径 dp[0][j]=1, dp[i][0]=1
// 而当有阻挡的时候,后面的格子都为0
// 确定遍历顺序 从左往右,从上往下
// 举例推导dp数组
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size(); // 获取数组的行数
int n = obstacleGrid[0].size(); // 获取数组的列数
vector<vector<int>> dp(m,vector<int>(n, 0)); //m行n列的二位数组vector
// 初始化
for(int i=0; i<m && obstacleGrid[i][0]==0; i++) dp[i][0]=1; // 第一列
// 当遇到障碍时,就不会再进行i++操作,所以后面格子都是0
for(int j=0; j<n && obstacleGrid[0][j]==0; j++) dp[0][j]=1; // 第一行
for(int i=1; i<m; i++){
for(int j=1; j<n; j++){
if(obstacleGrid[i][j]==0) // 当格子不为障碍时,路径进行相加
dp[i][j]= dp[i-1][j]+dp[i][j-1];
}
}
return dp[m-1][n-1];
}
};
文章来源:https://blog.csdn.net/m0_71413464/article/details/135730495
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 创建数据返回类型Result类
- 五、Spring AOP面向切面编程(基于注解方式实现和细节)
- All-Flash Array Key-Value Cache for Large Objects——论文泛读
- AI绘图制作红包封面教程
- CMake入门教程【核心篇】属性管理set_property和get_property
- spark基础--学习笔记
- flowable38张表含义说明以及一些操作指南
- 手把手教你制作微信图书小程序商城
- nginx.conf 文件配置
- 网络基础名词