寒假刷题-二分与前缀和

789. 数的范围

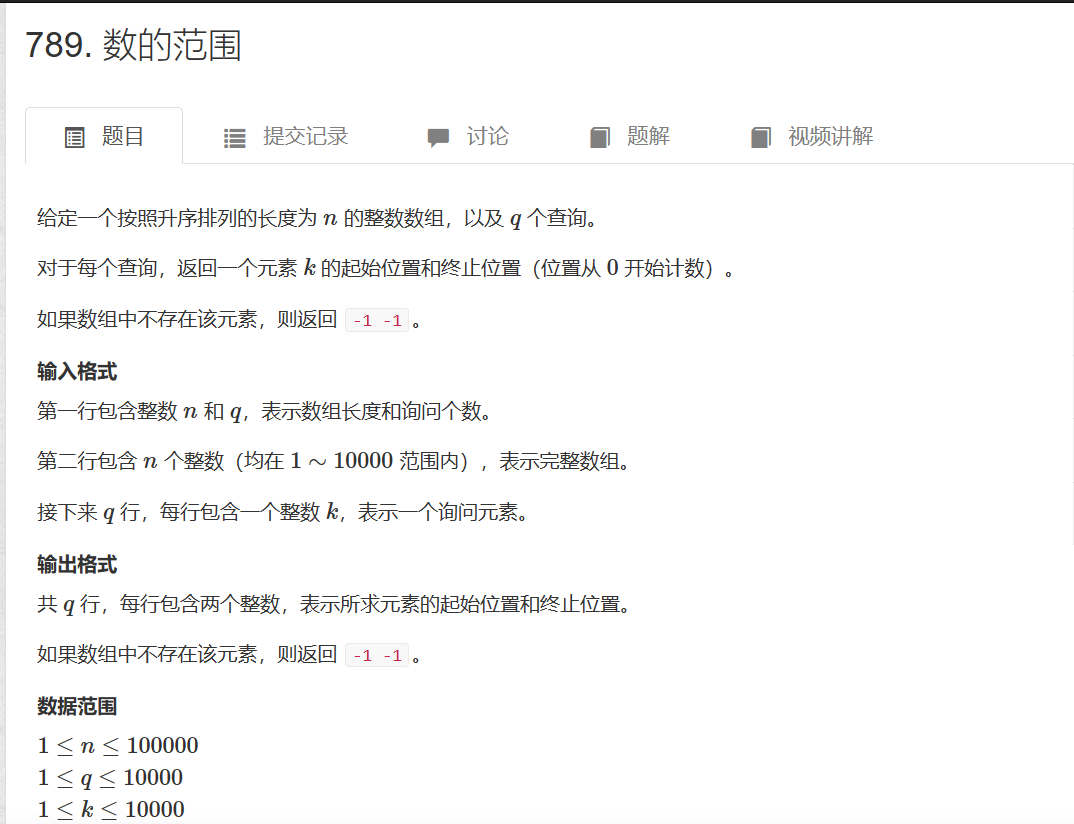
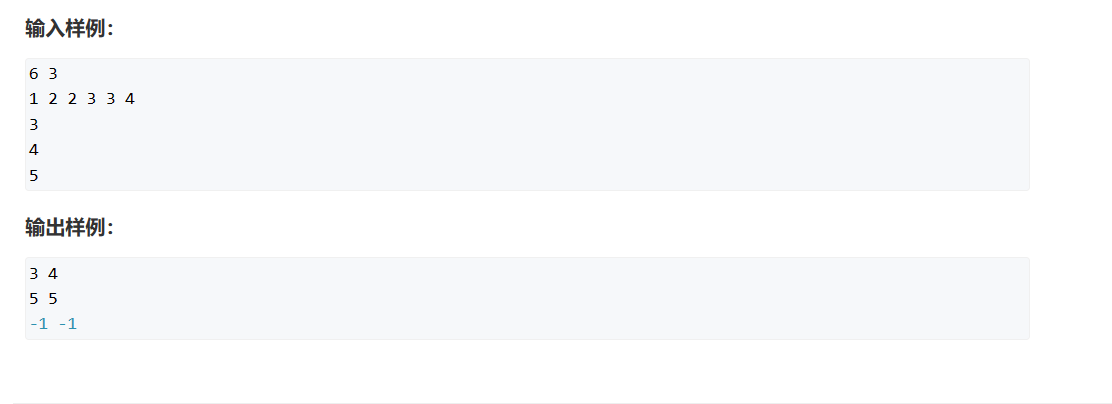
使用二分法来查找结果，因为数组是有序的，二分查找的时间复杂度是logN,查找q次就是q*logN。最大为10000 * 16 = 1.6e5小于1e8。二分法也叫折半查找，每次先找mid位置。看一下mid位置的数字和目标数字的关系，mid比目标数字的，说明mid后面那部分不可能存在目标值。将mid赋值给右边界。mid比目标小，mid左边不可能成为答案。将mid赋值给left。但是这种方法只是个大致思路。没有处理边界问题，也没有处理重复值返回最左边还是最右边的问题。

处理重复值
要找左边第一个与target接近的值，当midtarget时，将mid赋值给右边界
要找右边第一个与target接近的值，当midtarget时，将mid赋值给左边界

处理边界问题
当数组只有两个元素，第一个下标为0，第二个为1，1+0/2还是0。将mid赋值给左边界后会死循环。所以在找右边第一接近，更改l的时候，mid = l + r + 1 >> 1。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e6 + 10;
int arr[N];
int n,q,k,l,r,mid;
int main()
{
    scanf("%d%d",&n,&q);
    for(int i = 0;i < n;i ++)
    {
        scanf("%d",arr + i);
    }
    while(q --)
    {
        scanf("%d",&k);
        l = 0,r = n - 1;
        while(l < r)
        {
            mid = l + r >> 1;
            if(arr[mid] >= k) r = mid;
            else l = mid + 1;
        }
        if(arr[l] != k) cout << -1 <<" ";
        else cout << l <<" ";
        
         l = 0,r = n - 1;
        while(l < r)
        {
            mid = l + r + 1 >> 1;
            if(arr[mid] <= k) l = mid;
            else r = mid - 1;
        }
        if(arr[r] != k) cout << -1 << endl;
        else cout << r << endl;
    }
}

790. 数的三次方根 - AcWing题库

?

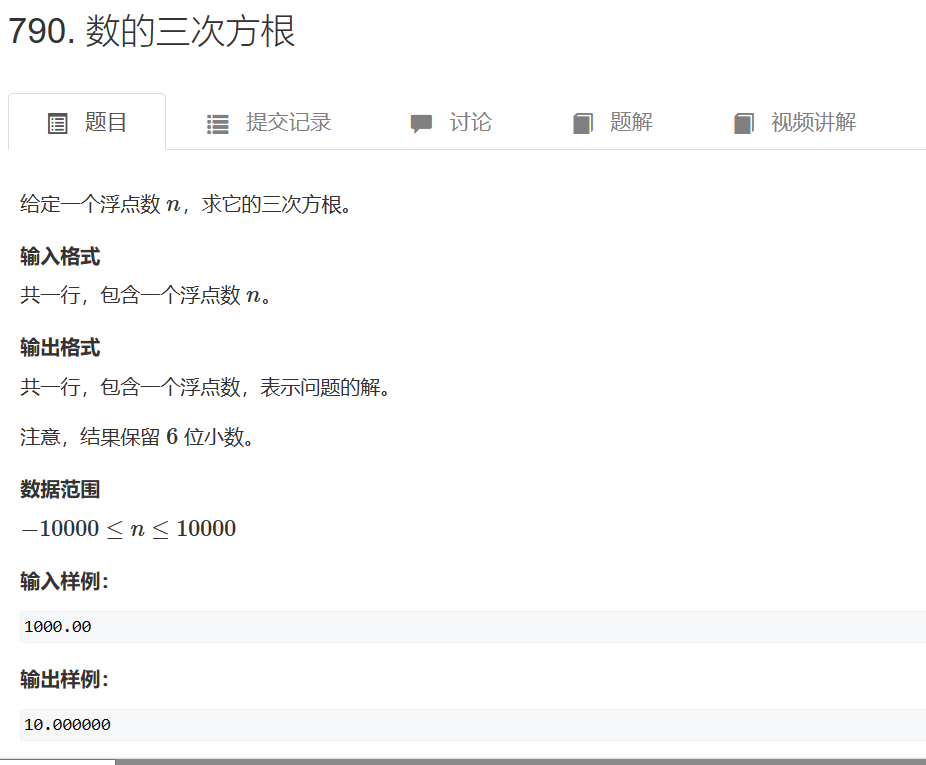
使用浮点数二分，题目要求保留六位，那二分的条件就写while(r-l>1e-8),当右边界与左边界的差值大于1e-8，比如说1.23333334和1.23333335这俩是都满足题意的。1e-8就是0.00000001。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
double n;
int main()
{
    cin >> n;
    double l = -1000,r = 1000,mid;
    while(r - l > 1e-8)
    {
        mid = (l + r) / 2;
        // cout << mid << endl;
        if(mid * mid * mid <= n)
        {
            l = mid;
        }
        else if(mid * mid * mid > n)
        {
            r = mid;
        }
      
    }
    printf("%lf",r);
    return 0;
}

因为答案唯一，等于号放哪都行。不写也是可以的。

795. 前缀和 - AcWing题库

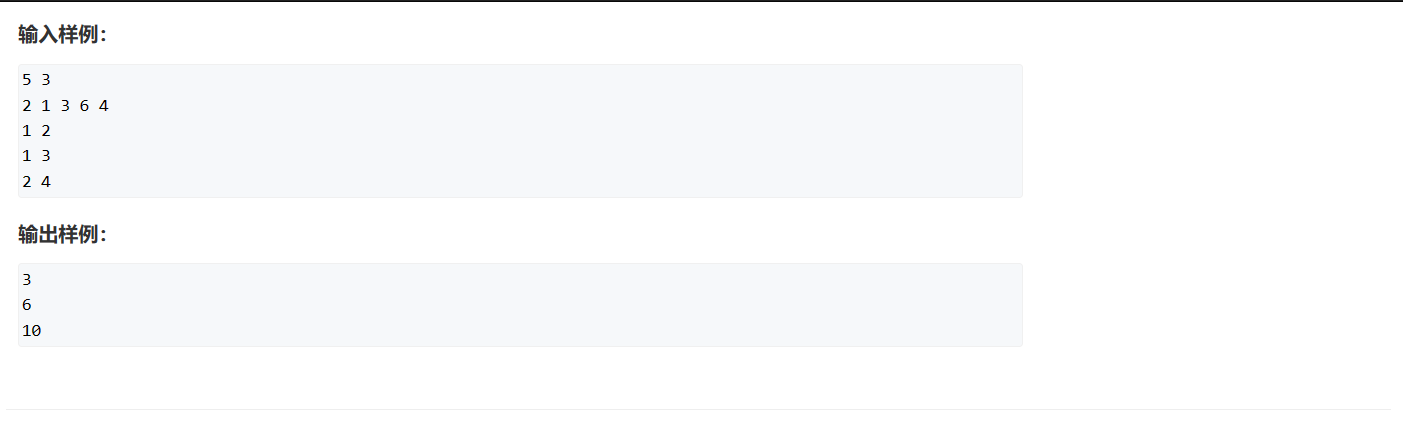
如果使用普通的算法，时间复杂度为O(m * n)最高为1e10，超过了1e8，会超时。使用前缀和优化算法。前缀数组下标从1开始，代表前i项的元素之和，想求j到i的元素之和，需要arr[i]-arr[j - 1]即可。

#include<cstdio>
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int q[N],ans[N];
int n,m,l,r;
int main()
{
    scanf("%d%d",&n,&m);
    for(int i = 1;i <= n;i ++)
    {
        scanf("%d",q + i);
    }
    for(int i = 1;i <= n;i ++)
    {
        ans[i] = q[i] + ans[i - 1];
    }
    while(m--)
    {
        scanf("%d%d",&l,&r);
        cout << ans[r] - ans[l - 1] <<endl;
    }
}

796. 子矩阵的和 - AcWing题库

二位前缀和与一维前缀和相比更为复杂。sij = si-1j+sj-1i-si-1j-1+qij。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1001;
int ans[N][N],q[N][N];
int n,m,c,x1,x2,y1,y2;
int main()
{
    scanf("%d%d%d",&n,&m,&c);
    for(int i = 1;i <= n;i ++)
    {
        for(int j = 1;j <= m;j ++)
        {
            scanf("%d",&q[i][j]);
        }
    }
    for(int k = 1;k <= m;k ++)
    {
        ans[1][k] = ans[1][k - 1]+q[1][k];
    }
     for(int k = 1;k <= n;k ++)
    {
        ans[k][1] = ans[k - 1][1]+q[k][1];
    }
    for(int i = 2;i <= n;i ++)
    {
        for(int j = 2;j <= m;j ++)
        {
            ans[i][j] = ans[i-1][j] + ans[i][j-1] - ans[i - 1][j - 1] + q[i][j];
        }
    }
    while(c --)
    {
        scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
        printf("%d\n",ans[x2][y2]-ans[x1-1][y2]-ans[x2][y1-1]+ans[x1-1][y1-1]);
    }
    // 1 1 2 2
    // 2 2 1 2 2 1  1 1
}

730. 机器人跳跃问题 - AcWing题库

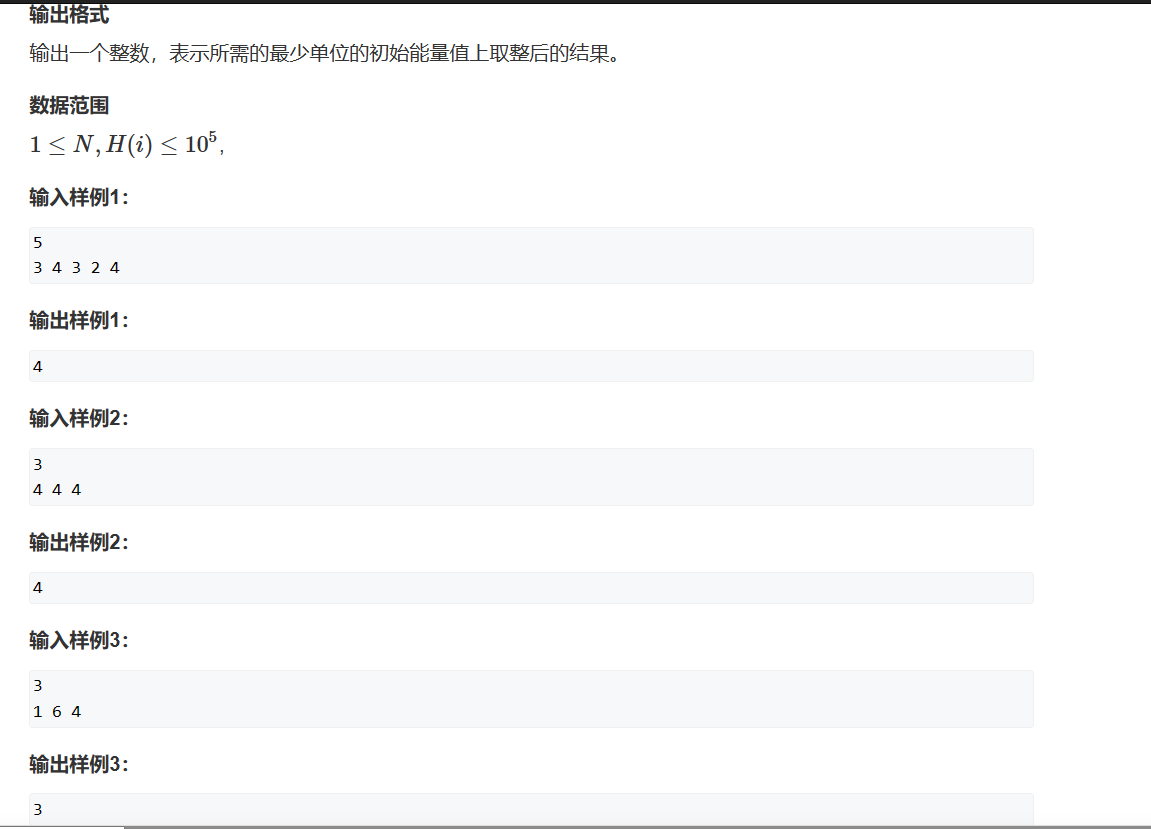
每个台阶都有能量，跳过这个台阶，如果总能量E大于这个台阶的能量H(i),那么总能量会减少H(i)-E，如果总能量大于H(i),总能量会增加E-H(i),两者整合以下公式会发现公式是一样的。

在跳台阶前的能量小于下一个台阶
$$E_i=E_{i?1}?(H_{(i)}?E_{i?1})$$
在跳台阶前的能量大于下一个台阶
$$E_i=E_{i?1}+E_{i?1}?H_{(i)}$$
总结就是
$$

$$

$$E_i=2E_{i?1}?H_{(i)}$$

问题是保证过程中Ei不小于0的最小初始能量为多少。

我们可以对答案E0进行二分，当满足条件时将mid赋值给有边界，不满足时将mid赋值给左边界+1。

 while(l < r)
    {
        mid = l + r >> 1;
        if(check(mid)) r = mid;
        else l = mid + 1;
    }

check函数用来判断过程中能量是否有出现小于0的情况，如果有说明这个初始能量不满足返回false，否则返回true.
但是check函数中，不能使用全程使用long long类型来存储，因为会超。通过公式我们可以发现，当Ei大于花费能量最大的台阶后，以后的台阶都是呈递增的，所以在check函数中判断当mid > 1e5,直接返回true。

#include<algorithm>
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int q[N],n;
bool check(int mid)
{
    for(int i = 0;i < n;i ++)
    {
        mid = 2 * mid - q[i];
        if(mid < 0) return false;
        if(mid > 1e5)return true;
    }
    return true;
}
int main()
{
    scanf("%d",&n);
    for(int i = 0;i < n;i ++)
    {
        scanf("%d",q + i);
    }
    int l = 0,r = 1e5 + 10,mid;
    while(l < r)
    {
        mid = l + r >> 1;
        if(check(mid)) r = mid;
        else l = mid + 1;
    }
    cout << l << endl;
}

1221. 四平方和 - AcWing题库

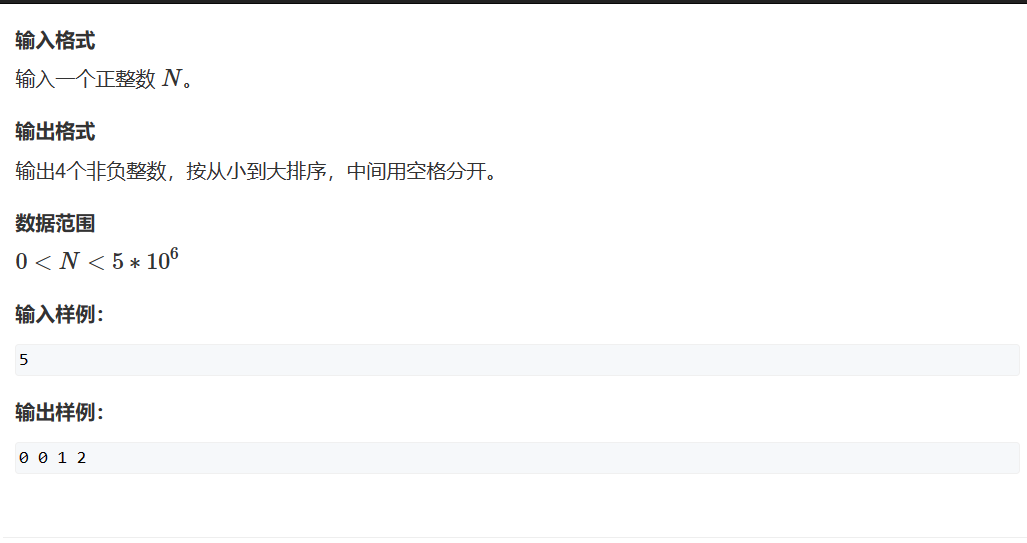
使用一个结构体数组存储所有可能a b 与 N-a^2-b2。然后对结构体数组按N-a^2-b2进行排序，然后外层循环从0开始，内层循环从i开始进行二分。如果q[mid]>=des令r=mid否则l=mid + 1

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
const int N = 5e6 + 10;
struct sum{
    int s,c,d;
   bool operator<(const sum &t)const
    {
        if(s != t.s) return s < t.s;
        if(c != t.c) return c < t.c;
        return d < t.d;
    }
};
sum re[N * 2];
int n,m;
int main()
{
    scanf("%d",&n);
    for(int c = 0;c * c <= n;c ++)
    {
         for(int d = c;c * c + d * d <= n;d ++)
         {
                   re[m ++] = {c * c + d * d,c,d};
         }
    }
    sort(re,re + m);
    // for(int i = 0;i < 15;i ++)
    // {
    //     printf("%d %d %d\n",re[i].s,re[i].c,re[i].d);
    // }
    
    for(int a = 0;a * a <= n;a ++)
    {
      for(int b = a;b * b + a * a <= n;b ++)
      {
                 int l = 0,r = m - 1,mid;
          int des = n -a * a - b * b;
        //   printf("%d\n",des);
          while(l < r)
          {
              mid = l + r >> 1;
              if(re[mid].s >=des) r = mid;
              else l = mid + 1;
          }
          if(re[l].s == des)
          {
              printf("%d %d %d %d",a,b,re[l].c,re[l].d);
                return 0;
          }
          
      }
    }
    return 0;
}

1227. 分巧克力 - AcWing题库

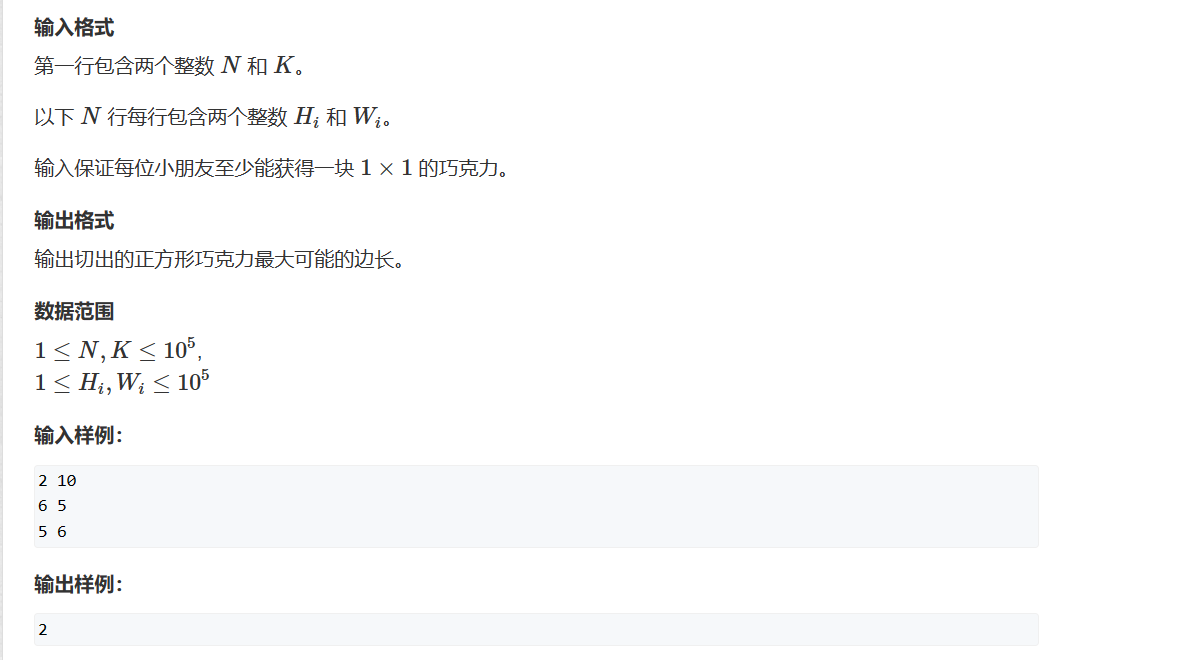
一块长为W宽为H的巧克力可以分成k块边长为x的巧克力
$$x=W/x+H/x$$
可以对巧克力的边长进行二分，check函数写对所有的w的h是否能满足分成k块蛋糕。如果cheak函数满足，那说明蛋糕店长度还可以变大，将mid赋值给l，如果不满足，说明蛋糕太大了，将mid - 1赋值给 r.

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,k;
const int N = 1e5 + 10;
int h[N],w[N];
bool check(int mid)
{
    int res = 0;
    for(int i = 0;i < n;i ++)
    {
        res += (h[i]/mid) * (w[i]/mid);
        if(res >= k) return true;
    }
    return false;
}
int main()
{
    cin >> n >> k;
    for(int i = 0;i < n;i ++)
    {
        cin >> h[i] >> w[i];
    }
    int l = 1,r = 1e5,mid;
    while(l < r)
    {
        mid = l + r + 1 >> 1;
        if(check(mid)) l = mid;
        else r = mid - 1;
    }
    cout << l << endl;
    return 0;
}

1230. K倍区间 - AcWing题库

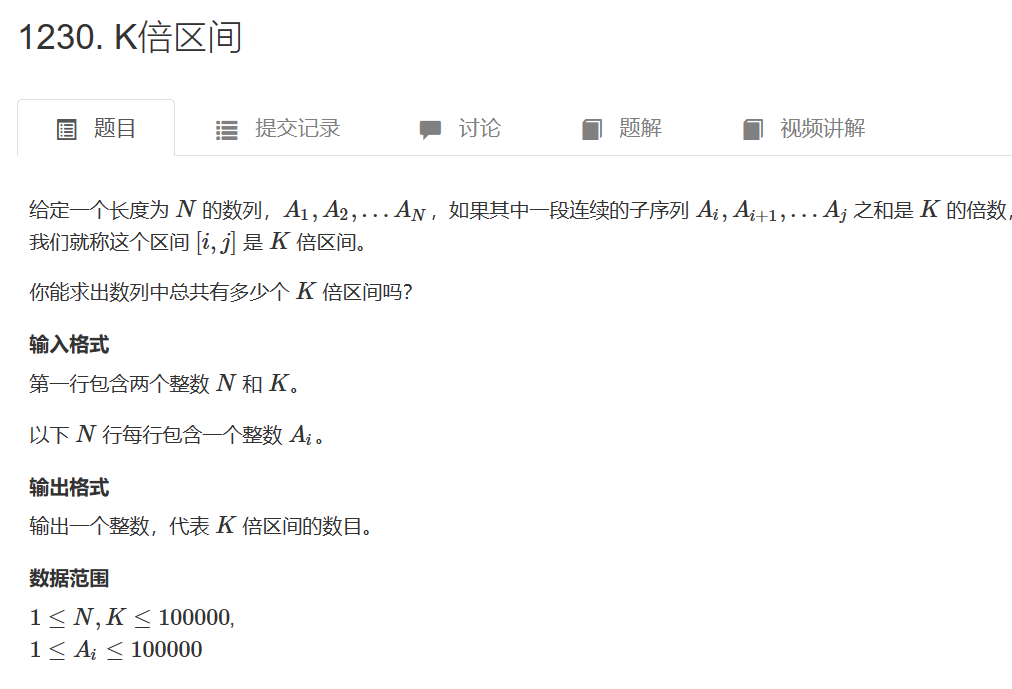
可以使用双层前缀和判断，时间复杂度为O(n * n)也就是1e10,远超1e8会超时，所以使用优化后的前缀和算法。

i到j的和可以整除可以写成
$$(a[j]?a[i?1])modk==0$$
可以使用ans[s[i]%k]来记录。a%3 == b %3 等价于上面的公式

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1e6 + 10;
int n,k;
long long s[N];
long long ans[N];
int main()
{
    cin >> n >> k;
    for(int i = 1;i <= n;i ++)
    {
        scanf("%lld",s + i);
    }
    for(int i = 1;i <= n;i ++)
    {
        s[i] += s[i - 1] ;
    }
    long long res = 0;
    
    ans[0] = 1;
    for(int i = 1;i <=n;i ++)
    {
        res += ans[s[i]%k];
        ans[s[i]%k] ++;
    }
    cout << res << endl;
    return 0;
}