绕某个点旋转
发布时间:2024年01月09日
1、首先推导绕原点旋转
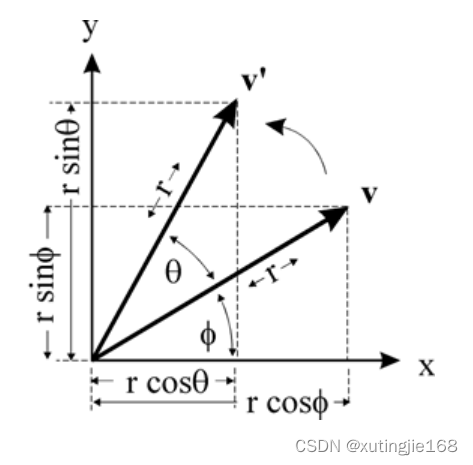
假设 v点的坐标是(x, y) ,那么可以推导得到 v’点的坐标(x’, y’)(设原点到v的距离是r
v’(x’, y’)
x′=r*cos(θ+?)
y′=r*sin(θ+?)
通过三角函数展开得到
x′=r*cosθcos??r*sinθsin?
y′=r*sinθcos?+r*cosθsin?
有因为
v(x,y)
x=r*cos?;
y=r*sin?;
带入
x′=r*cosθcos??r*sinθsin?
y′=r*sinθcos?+r*cosθsin?
所以旋转θ后的坐标如下
x′=x*cosθ?y*sinθ
y′=x*sinθ+y*cosθ
写成矩阵的形式如下
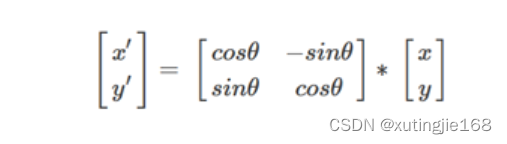
2、首先推导不在原点旋转

点V(x,y)绕点O(x0,y0)得到新的点V’(x',y');
V和V‘原点平移了(x0,y0)?
得到的新坐标
V(x-x0,y-y0)
V'(x'-x0,y'-y0)
没有平移之前
x′=x*cosθ?y*sinθ
y′=x*sinθ+y*cosθ
平移(x0,y0)?
x′-x0=(x-x0)*cosθ?(y-y0)*sinθ
y′-y0=(x-x0)*sinθ+(y-y0)*cosθ
得到
x'=(x-x0)*cosθ?(y-y0)*sinθ+x0;
y'=(x-x0)*sinθ+(y-y0)*cosθ+y0;
成下面矩阵的形式

实现代码:
struct point
{
double x;
double y;
};
point AfterPoint(point A,point B,double phi)
{
//任意点A(x1,y1),绕一个坐标点B(x2,y2)逆时针旋转θ角度后,新的坐标设为C(x, y)
//x= (x1 - x2)*cos(θ) - (y1 - y2)*sin(θ) + x2 ;
//y= (x1 - x2)*sin(θ) + (y1 - y2)*cos(θ) + y2 ;
//旋转的phi弧度
point C;
C.x = (A.x - B.x)*std::cos(phi) - (A.y - B.y)*std::sin(phi) + B.x;
C.y = (A.x - B.x)*std::sin(phi) + (A.y - B.y)*std::cos(phi) + B.y;
return C;
}
文章来源:https://blog.csdn.net/qq_36786800/article/details/135471715
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- c语言-结构体
- Java 第十一章(一)
- Java设计模式中策略模式可以解决许多if-else的代码结构吗? 是否能满足开闭原则?
- SQL注入思路基础
- 安达发|APS计划排产排程排单软件功能解析
- 负载开关IC——PC9511/21可编程高精度限流集成28mΩ功率FET外围只需极少元器件
- 黑马学成在线项目bug记录
- 【Nessus】容器化使用Nessus网络漏洞扫描工具
- ABS210-ASEMI手机适配器整流桥ABS210
- 基于springboot生鲜交易系统源码和论文