【第一章】数字信号处理之绪论 基础必备知识
对应程佩青《数字信号处理教程》第一章 绪论，对一些其它课程没有涉及的知识点进行总结，在之后的学习中它们是基础。
 ] = y ( n ) ? { T [ x ( n ? m ) ] = y ( n ? m ) ，移不变 T [ x ( D n ) ] = y ( D n ) ，线性 T[x(n)]=y(n)\leftrightarrow \begin{cases}T[x(n-m)]=y(n-m)，移不变\\T[x(Dn)]=y(Dn)，线性\end{cases} T[x(n)]=y(n)?{T[x(n?m)]=y(n?m)，移不变T[x(Dn)]=y(Dn)，线性?，为线性移不变系统LSI。
T
[
]
T[]
T[]是一个算子，类比于映射关系
f
:
y
=
f
(
x
)
f:y=f(x)
f:y=f(x)，不能将其等同于
y
(
n
)
y(n)
y(n)，我们要判断的是
x
(
n
′
)
x(n')
x(n′)通过
T
[
]
T[]
T[]的结果是否与
y
(
n
′
)
y(n')
y(n′)相同（输入移位/加权后通过系统的结果是否与此前的输出直接移位/加权的结果相同）
输入
x
(
n
)
x(n)
x(n)经过算子（系统）后的
y
(
n
)
y(n)
y(n)只变n，不改符号，不动常数，则为LSI系统。
通过下面的两个例子能够很好地理解LSI系统的判定准则
程佩青《数字信号处理教程》（第五版）中第32页的例1.14给出了一种判定准则
这里的
y
(
n
)
y(n)
y(n)实际上只是表示
y
y
y是关于
n
n
n的函数，回顾
y
=
f
(
x
)
y=f(x)
y=f(x)没有
y
(
x
)
y(x)
y(x)的说法，因此对经过系统后的结果
y
(
n
)
=
T
[
x
(
n
)
]
y(n)=T[x(n)]
y(n)=T[x(n)]进行平移是将整个
n
n
n作代换，不同于序列
x
(
n
)
x(n)
x(n)或
y
(
n
)
y(n)
y(n)的移位。
再看同一本书第57页配套的习题1.6(5)
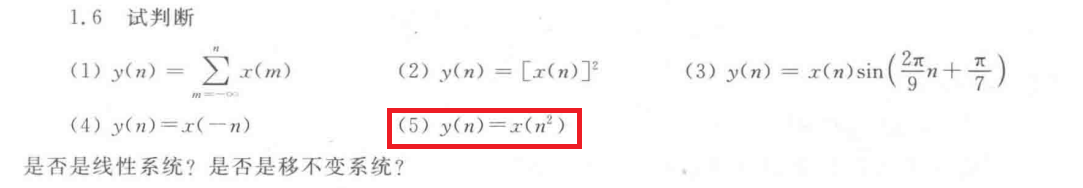
配套出版的《数字信号处理教程习题分析与解答》却告诉我们
y
(
n
)
=
x
(
n
2
)
y(n)=x(n^2)
y(n)=x(n2)为线性移不变系统，这似乎与上一道例题的判定准则给出的结论是相悖的。
按照上一道题的思路，设 y 1 ( n ) = x 1 ( n 2 ) y_1(n)=x_1(n^2) y1?(n)=x1?(n2)，对于输入 x 1 ( n ) x_1(n) x1?(n)移动 m m m位得新的输入 x 2 ( n ) = x 1 ( n ? m ) x_2(n)=x_1(n-m) x2?(n)=x1?(n?m)，则 y 2 ( n ) = x 2 ( n 2 ) = x 1 ( n 2 ? m ) y_2(n)=x_2(n^2)=x_1(n^2-m) y2?(n)=x2?(n2)=x1?(n2?m)，而 y 1 ( n ? m ) = x 1 [ ( n ? m ) 2 ] y_1(n-m)=x_1[(n-m)^2] y1?(n?m)=x1?[(n?m)2]，有 y 2 ( n ) ≠ y 1 ( n ? m ) y_2(n)\ne y_1(n-m) y2?(n)=y1?(n?m)，似乎并不是移不变系统。
如果将输入
x
(
n
)
x(n)
x(n)看作/换作
x
(
n
2
)
x(n^2)
x(n2)，则可参考下面的答案。
线性移不变系统的应用-单位冲激响应
我们知道
x
(
n
)
=
x
(
n
)
?
δ
(
n
)
=
∑
m
=
?
∞
∞
x
(
m
)
δ
(
n
?
m
)
\begin{aligned}x(n)=&x(n)*\delta(n)\\=&\sum_{m=-\infty}^{\infty}x(m)\delta(n-m)\end{aligned}
x(n)==?x(n)?δ(n)m=?∞∑∞?x(m)δ(n?m)?
对于每一项
x
(
m
)
δ
(
n
?
m
)
x(m)\delta(n-m)
x(m)δ(n?m)，对于卷积结果
y
(
n
)
=
x
(
n
)
=
x
(
n
)
?
δ
(
n
)
y(n)=x(n)=x(n)*\delta(n)
y(n)=x(n)=x(n)?δ(n)，
x
(
m
)
x(m)
x(m)与
n
n
n无关，其实为常数，看作
δ
(
n
?
m
)
\delta(n-m)
δ(n?m)的线性加权因子。而
δ
(
n
?
m
)
\delta(n-m)
δ(n?m)可以看作是
δ
(
n
)
\delta(n)
δ(n)的移位结果，是系统真正要处理的输入，由LSI系统的移不变性得
L
[
δ
(
n
?
m
)
]
=
h
(
n
?
m
)
L[\delta(n-m)]=h(n-m)
L[δ(n?m)]=h(n?m)，引出单位冲激响应。
每一项由LSI系统的线性性质的比例性可得
L
[
x
(
m
)
δ
(
n
?
m
)
]
=
x
(
m
)
L
[
δ
(
n
?
m
)
]
L[x(m)\delta(n-m)]=x(m)L[\delta(n-m)]
L[x(m)δ(n?m)]=x(m)L[δ(n?m)]
对于整个累加结果由线性的可加性得到
L
[
x
(
n
)
]
=
∑
m
=
?
∞
∞
x
(
m
)
h
(
n
?
m
)
=
x
(
n
)
?
h
(
n
)
L[x(n)]=\sum_{m=-\infty}^{\infty}x(m)h(n-m)=x(n)*h(n)
L[x(n)]=∑m=?∞∞?x(m)h(n?m)=x(n)?h(n)
因果系统和稳定系统
判断是否为因果系统的方法–冲激响应h(n)为因果系统
当n<0时，h(n)=0
y
(
n
)
=
x
(
n
)
?
h
(
n
)
=
∫
m
=
?
∞
∞
x
(
m
)
h
(
n
?
m
)
d
m
=
∫
m
=
?
∞
n
x
(
m
)
h
(
n
?
m
)
d
m
\begin{aligned}y(n)&=x(n)*h(n)\\&=\int_{m=-\infty}^{\infty}x(m)h(n-m)dm\\&=\int_{m=-\infty}^{n}x(m)h(n-m)dm\end{aligned}
y(n)?=x(n)?h(n)=∫m=?∞∞?x(m)h(n?m)dm=∫m=?∞n?x(m)h(n?m)dm?
故y(n)的值由小于n的m值来决定，符合因果系统定义
判断系统稳定的方法是判断冲激序列h(n)是否满足绝对可和
∑
n
=
?
∞
∞
∣
h
(
n
)
∣
=
P
<
∞
\sum_{n=-\infty}^{\infty}|h(n)|=P<\infty
∑n=?∞∞?∣h(n)∣=P<∞
系统稳定：有界输入，产生有界输出
证明：若不满足，
∑
n
=
?
∞
∞
∣
h
(
n
)
∣
=
∞
\sum_{n=-\infty}^{\infty}|h(n)|=\infty
∑n=?∞∞?∣h(n)∣=∞
设
x
(
n
)
=
{
1
h
(
?
n
)
≥
0
?
1
h
(
?
n
)
<
0
x(n)=\begin{cases}1&h(-n)\ge 0\\-1&h(-n)<0\end{cases}
x(n)={1?1?h(?n)≥0h(?n)<0?
y
(
n
)
=
x
(
n
)
?
h
(
n
)
=
∑
m
=
?
∞
∞
x
(
m
)
h
(
n
?
m
)
y(n)=x(n)*h(n)=\sum_{m=-\infty}^{\infty}x(m)h(n-m)
y(n)=x(n)?h(n)=∑m=?∞∞?x(m)h(n?m)
y
(
0
)
=
∑
m
=
?
∞
∞
x
(
m
)
h
(
?
m
)
=
∑
m
=
?
∞
∞
∣
h
(
?
m
)
∣
=
∞
y(0)=\sum_{m=-\infty}^{\infty}x(m)h(-m)=\sum_{m=-\infty}^{\infty}|h(-m)|=\infty
y(0)=∑m=?∞∞?x(m)h(?m)=∑m=?∞∞?∣h(?m)∣=∞
卷积和的求法
三种求法
解析+图解法
写成
y
(
n
)
=
∑
m
=
?
∞
∞
x
(
m
)
h
(
n
?
m
)
y(n)=\sum_{m=-\infty}^{\infty}x(m)h(n-m)
y(n)=∑m=?∞∞?x(m)h(n?m)的形式
h相当于反折+移位，如果两者都不是有限长可以分为三种情况（画图更好判断）
- 反折后“左减右加”，故当n小于一定值（为负数）时，h整体移动到了x的左侧，两者无交集，卷积和为零
- 当h的右端与x有交集，但没有覆盖整个x时，m的上限取到m，下限由x的下限决定
- 当n大于某个数，h的左端已经移动到了x的左端的右端，完全重合，上下限完全固定，与n无关，分h的右侧是否在x的右侧里外两种情况讨论，实际上是四种情况
列表法
固定m根据函数的界限确定有限个n，列出两个函数的值相乘，同一个n对应的累加得结果
对位相乘相加法
实质上是列表法的简化，讲两个序列的右端对齐，进行类似竖式乘法，直接加得y(n)结果，再根据两个序列的范围确定卷积和结果的范围，来确定原点。
（不需要反转x或者h，m值固定而n从小变大，观察表格相当于n从左向右移动，但进行运算的位固定在右端，如果重新排序的话相当于反转了序列 ）
卷积和范围确定
x
(
n
)
:
N
1
≤
n
≤
N
2
x(n):N_1\le n \le N_2
x(n):N1?≤n≤N2? 长度为N
y
(
n
)
:
N
3
≤
n
≤
N
4
y(n):N_3\le n \le N_4
y(n):N3?≤n≤N4? 长度为M
则
h
(
n
)
:
N
1
+
N
3
≤
n
≤
N
2
+
N
4
h(n):N_1+N_3\le n \le N_2+N_4
h(n):N1?+N3?≤n≤N2?+N4? 长度为N+M-1
运用到了“右加”的性质，或直接根据定义式有值判断
典型序列
- 冲激序列 δ ( n ) = { 1 n = 0 0 n ≠ 0 \delta (n)=\begin{cases}1&n=0\\0&n\ne 0\end{cases} δ(n)={10?n=0n=0?
- 矩形序列 R N ( n ) = u ( n ) ? u ( n ? N ) R_N(n)=u(n)-u(n-N) RN?(n)=u(n)?u(n?N)，在0到N-1上有值
- 正弦序列 x ( n ) = A s i n ( w 0 n + ? ) x(n)=Asin(w_0n+\phi) x(n)=Asin(w0?n+?)
正弦序列的频率
数字频率和模拟角频率
数字频率
w
0
w_0
w0?，单位为rad
模拟角频率
Ω
0
\Omega_0
Ω0?，单位为rad/s
w
=
Ω
T
=
Ω
f
s
=
2
π
f
f
s
w=\Omega T=\frac{\Omega}{f_s}=\frac{2\pi f}{f_s}
w=ΩT=fs?Ω?=fs?2πf?
抽样频率
f
s
f_s
fs?，
x
(
n
)
=
x
a
(
n
T
)
x(n)=x_a(nT)
x(n)=xa?(nT)
正弦序列的周期性
要使
x
(
n
+
N
)
=
A
c
o
s
[
w
0
(
n
+
N
)
+
?
]
=
x
(
n
)
x(n+N)=Acos[w_0(n+N)+\phi]=x(n)
x(n+N)=Acos[w0?(n+N)+?]=x(n)
则
w
0
N
=
2
k
π
w_0N=2k\pi
w0?N=2kπ
N
=
2
π
w
0
k
=
f
0
f
s
k
N=\frac{2\pi}{w_0}k=\frac{f_0}{f_s}k
N=w0?2π?k=fs?f0??k
n和N为整数，k也为整数，就要求
2
π
w
0
\frac{2\pi}{w_0}
w0?2π?为整数
- 若 2 π w 0 \frac{2\pi}{w_0} w0?2π?为整数， k 2 π w 0 k\frac{2\pi}{w_0} kw0?2π?为最小正周期
- 若 2 π w 0 = p q \frac{2\pi}{w_0}=\frac{p}{q} w0?2π?=qp?为有理数，则最小正周期为 q 2 π w 0 = p q\frac{2\pi}{w_0}=p qw0?2π?=p,N不是整数
- 若为无理数，非周期
理想抽样信号的频谱
理想抽样信号
x
^
a
(
t
)
=
x
a
(
t
)
?
δ
T
(
t
)
=
x
a
(
t
)
∑
m
=
?
∞
∞
δ
(
t
?
m
T
)
=
∑
m
=
?
∞
∞
x
a
(
m
T
)
δ
(
t
?
m
T
)
\begin{aligned}\hat{x}_a(t)=&x_a(t)\cdot\delta_T(t)\\=&x_a(t)\sum_{m=-\infty}^{\infty}\delta(t-mT)\\=&\sum_{m=-\infty}^{\infty}x_a(mT)\delta(t-mT)\end{aligned}
x^a?(t)===?xa?(t)?δT?(t)xa?(t)m=?∞∑∞?δ(t?mT)m=?∞∑∞?xa?(mT)δ(t?mT)?
由傅里叶变换的时域相乘性质得
X
^
a
(
j
Ω
)
=
1
2
π
X
a
(
j
Ω
)
?
F
T
[
δ
T
(
t
)
]
\hat{X}_a(j\Omega)=\frac{1}{2\pi}X_a(j\Omega)*FT[\delta_T(t)]
X^a?(jΩ)=2π1?Xa?(jΩ)?FT[δT?(t)]
求周期函数的傅立叶变换先求其傅立叶级数系数
δ
T
(
t
)
=
∑
k
=
?
∞
∞
A
k
e
j
k
Ω
s
t
\delta_T(t)=\sum_{k=-\infty}^{\infty}A_ke^{jk\Omega_st}
δT?(t)=∑k=?∞∞?Ak?ejkΩs?t
则
A
k
=
1
T
∫
?
T
2
T
2
δ
T
(
t
)
e
?
j
k
Ω
s
t
d
t
=
1
T
∫
?
T
2
T
2
∑
m
=
?
∞
∞
δ
(
t
?
m
T
)
e
?
j
k
Ω
s
t
d
t
=
1
T
∫
?
T
2
T
2
δ
(
t
)
e
?
j
k
Ω
s
t
d
t
（只在一个周期内积分）
=
1
T
\begin{aligned}A_k=&\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}\delta_T(t)e^{-jk\Omega_st}dt\\=&\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}\sum_{m=-\infty}^{\infty}\delta(t-mT)e^{-jk\Omega_st}dt\\=&\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}\delta(t)e^{-jk\Omega_st}dt（只在一个周期内积分）\\=&\frac{1}{T}\end{aligned}
Ak?====?T1?∫?2T?2T??δT?(t)e?jkΩs?tdtT1?∫?2T?2T??m=?∞∑∞?δ(t?mT)e?jkΩs?tdtT1?∫?2T?2T??δ(t)e?jkΩs?tdt（只在一个周期内积分）T1??
则其傅里叶变换为
F
T
[
1
T
∑
k
=
?
∞
∞
1
?
e
j
k
Ω
s
t
]
=
1
T
∑
k
=
?
∞
∞
F
T
[
1
?
e
j
k
Ω
s
t
]
=
1
T
∑
k
=
?
∞
∞
2
π
δ
(
Ω
?
Ω
s
)
=
2
π
T
∑
k
=
?
∞
∞
δ
(
Ω
?
Ω
s
)
=
Ω
s
∑
k
=
?
∞
∞
δ
(
Ω
?
Ω
s
)
\begin{aligned}&FT[\frac{1}{T}\sum_{k=-\infty}^{\infty}1\cdot e^{jk\Omega_st}]\\=&\frac{1}{T}\sum_{k=-\infty}^{\infty}FT[1\cdot e^{jk\Omega_st}]\\=&\frac{1}{T}\sum_{k=-\infty}^{\infty}2\pi\delta(\Omega-\Omega_s)\\=&\frac{2\pi}{T}\sum_{k=-\infty}^{\infty}\delta(\Omega-\Omega_s)\\=&\Omega_s\sum_{k=-\infty}^{\infty}\delta(\Omega-\Omega_s)\end{aligned}
====?FT[T1?k=?∞∑∞?1?ejkΩs?t]T1?k=?∞∑∞?FT[1?ejkΩs?t]T1?k=?∞∑∞?2πδ(Ω?Ωs?)T2π?k=?∞∑∞?δ(Ω?Ωs?)Ωs?k=?∞∑∞?δ(Ω?Ωs?)?
则
X
a
(
j
Ω
)
?
Ω
s
∑
k
=
?
∞
∞
δ
(
Ω
?
Ω
s
)
=
Ω
s
∑
k
=
?
∞
∞
X
a
[
j
(
Ω
?
k
Ω
s
)
]
\begin{aligned}&X_a(j\Omega)*\Omega_s\sum_{k=-\infty}^{\infty}\delta(\Omega-\Omega_s)\\=&\Omega_s\sum_{k=-\infty}^{\infty}X_a[j(\Omega-k\Omega_s)]\end{aligned}
=?Xa?(jΩ)?Ωs?k=?∞∑∞?δ(Ω?Ωs?)Ωs?k=?∞∑∞?Xa?[j(Ω?kΩs?)]?
X
^
a
(
j
Ω
)
=
1
2
π
X
a
(
j
Ω
)
?
F
T
[
δ
T
(
t
)
]
=
1
T
∑
k
=
?
∞
∞
X
a
[
j
(
Ω
?
k
Ω
s
)
]
\begin{aligned}\hat{X}_a(j\Omega)=&\frac{1}{2\pi}X_a(j\Omega)*FT[\delta_T(t)]\\=&\frac{1}{T}\sum_{k=-\infty}^{\infty}X_a[j(\Omega-k\Omega_s)]\end{aligned}
X^a?(jΩ)==?2π1?Xa?(jΩ)?FT[δT?(t)]T1?k=?∞∑∞?Xa?[j(Ω?kΩs?)]?
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码（1）
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【华为机试】2023年真题B卷（python）-计算最大乘积
- 【Redis】AOF 基础
- 【洛谷千题详解】P7072 [CSP-J2020] 直播获奖
- OpenCV-Python(41):背景减除
- 亚马逊请求评论模板怎么设置？如何有效请求评论？——站斧浏览器
- vue项目中使用vue-seamless-scroll遇到的坑
- 私域要做成交，离不开这5个核心
- 《从晨到夜：在日常繁忙中寻找成长与平衡的艺术》
- npm 抽取 解析（持续更新中）
- 自营商城与多商户入驻商城功能与开发流程_OctShop