你好!堆排序【JAVA】
发布时间:2023年12月17日

目录
1.简单介绍
堆排序是一种基于堆数据结构的排序算法,其核心思路是利用堆这种特殊的数据结构来对数据进行排序。堆是一种完全二叉树,并且满足父节点的值大于等于(或小于等于)其子节点的值。
2.大小顶堆?
 ?
?
- 大顶堆:当前节点的值大于其左子节点和右子节点的值
- 大顶堆特点:arr[i]>=arr[2*i+1] && arr[i]>=arr[2*i+2]
- 小顶堆:当前节点的值小于其左子节点和右子节点的值
- 小顶堆特点:arr[i]<=arr[2*i+1] && arr[i]<=arr[2*i+2]
注:升序采用大顶堆,降序采用小顶堆
?3.基本思想
- 1.建堆:首先将待排序的数组看作一棵完全二叉树,然后对树中每个非叶子节点进行堆化,即将其和其子节点的值进行比较,将较大(或较小)的值放到父节点上,然后递归地对子节点进行堆化,直到整个树变为一个堆。
- 2.排序:排序的过程就是不断将堆顶的元素(最大值或最小值)取出并放到已经排好序的数组的末尾,然后将堆进行调整,保证堆的性质不变。不断取出堆顶元素并进行调整,直到堆为空,排序完成。
4.基本思路
- 1.将无序序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
- 2.将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
- 3.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
4.代码实现数组转化堆
1.建堆
/**
* 将数组,调整一个大顶堆
*
* @param array:待调整的数组
* @param i:非叶子节点在数组中的索引
* @param length:表示对多少个元素进行调整,length逐减
*/
public static void adjustHeapSort(int[] array, int i, int length) {
int temp = array[i];//定义临时变量,保存当前值
//调整
//1.k=i*2+1:表示i节点的左子节点
for (int k = i * 2 + 1; k < length; k = i * 2 + 1) {
if (k + 1 < length && array[k] < array[k + 1]) {//说明左子节点小于右子节点
k++;//k指向右子节点
}
if (array[k] > temp) {//子节点大于父节点,进行交换
array[i] = array[k];//子节点赋给父节点
i = k;
} else {
break;
}
}
//结束for循环,已经将以i为父节点的树的最大值,放在了最顶端
array[i] = temp;//将temp放到最后调整的位置
}5.代码排序
2.排序
for (int j = array.length - 1; j > 0; j--) {
int temp = array[j];
array[j] = array[0];
array[0] = temp;
adjustHeapSort(array, 0, j);
}6.总代码+测试
public static void main(String[] args) {
int[] array = new int[]{4, 6, 8, 5, 9, 10, 7, -2};
heapSort(array);
}
public static void heapSort(int[] array) {
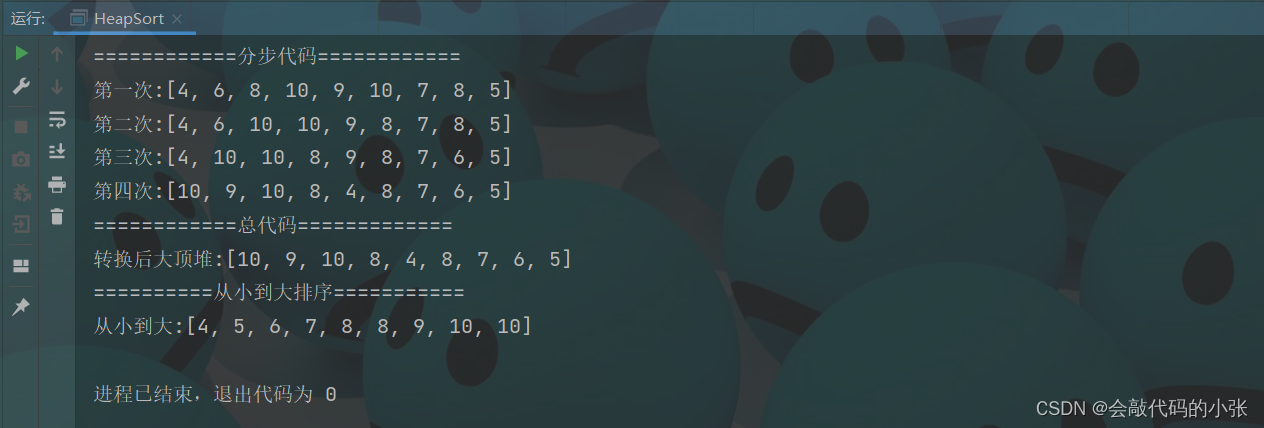
System.out.println("============分步代码============");
adjustHeapSort(array, 1, array.length);
System.out.println("第一次:" + Arrays.toString(array));
adjustHeapSort(array, 0, array.length);
System.out.println("第二次:" + Arrays.toString(array));
//数组转化大顶堆
System.out.println("============总代码=============");
for (int i = array.length / 2 - 1; i >= 0; i--) {
adjustHeapSort(array, i, array.length);
}
System.out.println("转换后大顶堆:" + Arrays.toString(array));
for (int j = array.length - 1; j > 0; j--) {
int temp = array[j];
array[j] = array[0];
array[0] = temp;
adjustHeapSort(array, 0, j);
}
System.out.println("==========从小到大排序===========");
System.out.println("从小到大:" + Arrays.toString(array));
}
/**
* 将数组,调整一个大顶堆
*
* @param array:待调整的数组
* @param i:非叶子节点在数组中的索引
* @param length:表示对多少个元素进行调整,length逐减
*/
public static void adjustHeapSort(int[] array, int i, int length) {
int temp = array[i];//定义临时变量,保存当前值
//调整
//1.k=i*2+1:表示i节点的左子节点
for (int k = i * 2 + 1; k < length; k = i * 2 + 1) {
if (k + 1 < length && array[k] < array[k + 1]) {//说明左子节点小于右子节点
k++;//k指向右子节点
}
if (array[k] > temp) {//子节点大于父节点,进行交换
array[i] = array[k];//子节点赋给父节点
i = k;
} else {
break;
}
}
//结束for循环,已经将以i为父节点的树的最大值,放在了最顶端
array[i] = temp;//将temp放到最后调整的位置
}


文章来源:https://blog.csdn.net/dfdg345/article/details/134934408
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- AI-数学-高中-4.函数表达式特性-要变一起变
- 【5G PHY】5G 物理层加速卡介绍
- Python Opencv实践 - 人体姿态检测
- Lombook快速入门
- 深度学习入门python考试速成:神经网络之前向传播
- android usb2.0 协议基础(3)
- 解释 Git 的基本概念和使用方式
- 智慧工地云平台源码 支持二次开发、支持源码交付
- 芯片制造流程简介
- 8.15 PowerBI系列之DAX函数专题-找出无购买行为的客户