ICLR 2024 Oral InfoBatch 助力大模型时代训练加速！FaceChain与NUS尤洋团队最新工作！

ICLR 2024 Oral | InfoBatch，三行代码，无损加速，即插即用！助力大模型时代训练加速！FaceChain与NUS尤洋团队最新工作。

FaceChain：https://github.com/modelscope/facechain。

随着深度学习的网络参数量和数据集规模增长，算力需求日益增加，如何节省训练成本正在成为逐渐凸显的需求。现有的数据集压缩方法大多开销较高，且难以在达到无损的情况下获得可观的节省率；加权抽样的相关方法则对于模型和数据集的特点较为敏感且依赖于重复抽样假设，在实际应用中难以和已完成调参的学习率调整策略结合。两种从数据角度出发的方法在实践中很难真正帮助节省计算。

在本篇工作中，研究者从数据迭代这个角度切入进行了研究。长久以来，数据集的迭代方式大都采用随机迭代。对此，作者提出了InfoBatch框架，根据网络对样本的拟合情况进行动态剪枝采样的方法，并利用重缩放（rescaling）来维持剪枝后的梯度更新（Gradient Update）期望，以此在性能无损的情况下提高训练效率，加快训练速度。

在CIFAR10/100、ImageNet-1K（分类）和ADE20K（语义分割）上，InfoBatch无损节省了40%的总开销（时间和计算）；在检测任务上，InfoBatch无损节省了30%；
对于MAE预训练和diffusion, InfoBatch分别节省了24.8%和27%的开销。
在LLaMA的指令微调上, InfoBatch成功节省了20%开销，并且和LoRA以及现有的核心集合选择(coreset selection)方法兼容。

论文题目：
InfoBatch: Lossless Training Speed Up by Unbiased Dynamic Data Pruning
论文地址：https://arxiv.org/abs/2303.04947
代码地址：https://github.com/henryqin1997/InfoBatch

一、动机

在过去的十年里，深度学习取得了长足的进步。与之相应的是大部分最先进的深度学习工作大都使用了超大规模的数据集，这对于很多资源有限的研究者来说是难以负担的。为了降低训练开销，研究者们进行了一系列不同研究。

一个比较直接的方法是降低数据集规模。数据集蒸馏（Dataset Distillation）[1]和核心集合选择（Coreset Selection）[2]分别从原有的数据集中合成/选择一个更小但更有信息量的新数据集（子集）。然而，虽然样本数量减少了，这两种方法本身却引入了不可忽略的额外开销。此外，这两种方法达到无损性能比较困难。另外的工作有加权抽样（weighted sampling）[3]，可以通过改变样本采样率来提高训练收敛速度，相应的缺点是加速比对模型和数据集敏感，难以直接和学习率调整策略结合。

近期，一些工作试图通过减少迭代来加速训练。其中一类方法和核心集合选择类似，通过给样本打分并排序来选取更有信息量的样本，其余样本不参加训练，作者称之为数据静态剪枝；另一类方法在此基础上，于训练过程中动态打分并周期性选取子集，作者称之为数据动态剪枝。相比于静态方法，动态方法的单次额外开销更小，而且同计算量性能更好，但是现有方法依旧难以达到无损性能。

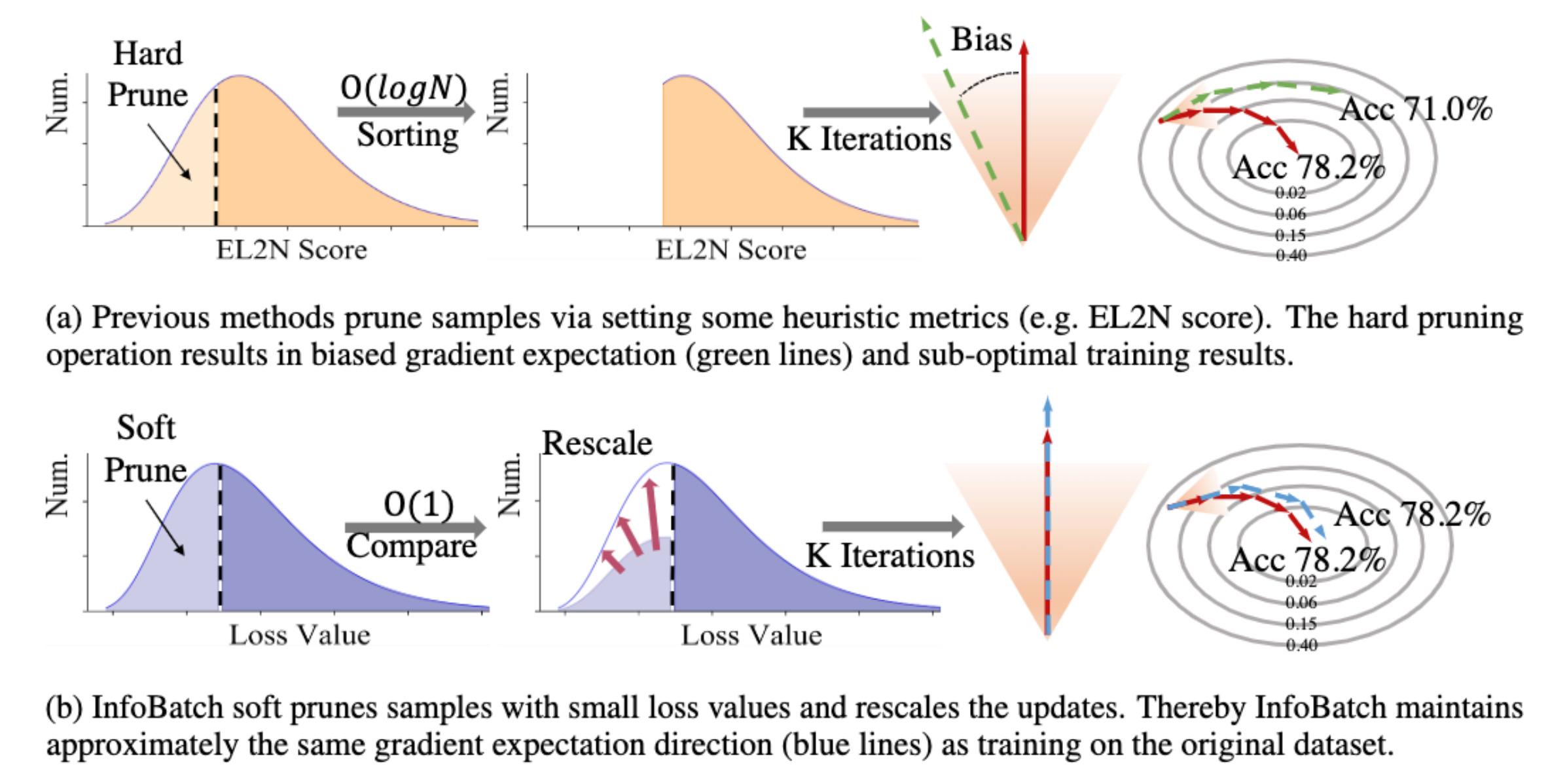
为了应对以上方法的缺点，作者提出了InfoBatch训练框架。InfoBatch的主要改进如图1所示，它在数据迭代过程中动态剪枝，通过Soft Pruning（概率剪枝）和Gradient Rescaling（梯度重缩放）维护了总更新量的期望值不变，以此达到了无损加速的目的。为了防止剩余训练轮次不足时的残余偏差，InfoBatch在最后的少部分轮次中使用原始数据集随机采样训练。作者在分类，语义分割，目标检测，Diffusion图片生成，LLaMA指令微调等任务上验证了方法的无损加速。

二、方法

2.1 总览

现有的静态/动态数据剪枝方法，会通过某种方式给样本打分，然后对样本得分排序，选取“对训练更有帮助”的样本进行训练。这种选择通常是确定性的，和目标的剪枝百分比直接挂钩。与之相对应的问题是，直接剪枝导致了梯度期望值方向偏差以及总更新量的减少。

为了解决梯度更新的期望偏差，如图2所示，InfoBatch前向传播中维护了每个样本的分值，并以均值为阈值，对一定比例的低分样本进行了动态剪枝。为了维护梯度更新期望，剩余的低分样本的梯度被相应放大。通过这种方式，InfoBatch训练结果和原始数据训练结果的性能差距相比于之前方法得到了改善。为了进一步减少残余的梯度期望值偏差，InfoBatch在最后几个轮次中使用全数据训练。

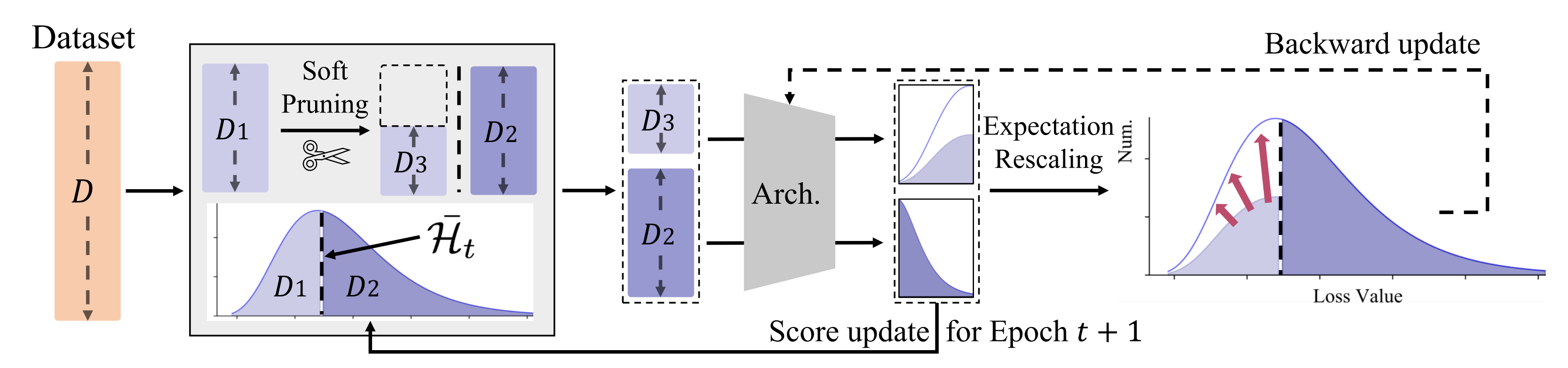
2.2 无偏剪枝和重缩放（Unbiased Prune and Rescale）

在训练的前向过程中，InfoBatch会记录样本的损失值（loss）来作为样本分数，这样基本没有额外打分的开销。对于首个epoch，InfoBatch初始化默认保留所有样本。之后的每个epoch开始前，InfoBatch会按照剪枝概率 $r$ 来随机对分数小于平均值的样本进行剪枝（保留概率为$1?r$）。概率式表达为
$${\mathcal{P}}_t(z)=\{\begin{array}{ll}r,& {\mathcal{H}}_t(z)<\overline{{\mathcal{H}}_t}\\ 0,& {\mathcal{H}}_t(z)\ge \overline{{\mathcal{H}}_t}\end{array}$$
其中${\mathcal{P}}_t(z)$是剪枝概率，$H_t(z)$是样本$z$在上一轮中的分数,$\overline{{\mathcal{H}}_t}$是上一轮分数的均值。

对于分数小于均值并留下参与训练的样本（$\mathcal{H}(z)<{\bar{\mathcal{H}}}_t$），InfoBatch采用了重缩放（rescaling），将对应梯度增大到了$1/(1?r)$。这使得整体更新是接近于无偏的。记原始数据集为$\mathcal{D}$，t时刻剪枝后的数据集为${\mathcal{S}}_t$,简短的证明如下：

原始的objective为
$$argmi{n}_{\theta \in \Theta }{\mathbb{E}}_{z\in \mathcal{D}}[\mathcal{L}(z,\theta )]={\int }_z\mathcal{L}(z,\theta )\rho (z)dz.$$

剪枝并重缩放后,每个样本的采样率为$(1?{\mathcal{P}}_t(z))\rho (z)$，缩放系数为${\gamma }_t(z)=1/(1?{\mathcal{P}}_t(z))$，objective变为
$$argmi{n}_{\theta \in \Theta }{\mathbb{E}}_{z\in {\mathcal{S}}_t}[{\gamma }_t(z)\mathcal{L}(z,\theta )]=argmi{n}_{\theta \in \Theta }\frac{1}{c_t}{\int }_z\mathcal{L}(z,\theta )\rho (z)dz$$

剪枝并重缩放后的优化目标和原始的优化目标有相同的解，因为给定时刻的$\frac{1}{c_t}$是一个常数系数。

其中
$$\mathbb{E}\left[\frac{1}{c_t}\right]=\frac{|\mathcal{D}|}{{\sum }_{z\in \mathcal{D}}(1?{\mathcal{P}}_t(z))}?\frac{|\mathcal{D}|}{|{\mathcal{S}}_t|}?\mathbb{E}[{?}_{\theta }\mathcal{L}({\mathcal{S}}_t)]?\frac{|\mathcal{D}|}{|{\mathcal{S}}_t|}\mathbb{E}[{?}_{\theta }\mathcal{L}(\mathcal{D})]$$

剪枝后的更新步数变为了原先的$\frac{|{\mathcal{S}}_t|}{|\mathcal{D}|}$，步长变为了原先的$\frac{|\mathcal{D}|}{|{\mathcal{S}}_t|}$，因此概率剪枝加重缩放的策略维护了更新量的总体基本一致。

2.3 退火（Annealing）

虽然理论上的期望更新基本一致，上述的期望值实际包含时刻t的多次取值。在训练中，如果一个样本在中间的某个轮次被剪枝，后续依旧大概率被训练到；而在剩余更新轮次不足时，这个概率会大幅下降，导致残余的梯度期望偏差。因此，在最后的几个训练轮次中（通常是12.5%~17.5%左右），InfoBatch采用完整的原始数据进行训练。

三、实验

3.1 实验设置

作者在多个数据集上验证了InfoBatch的有效性，包括（分类）CIFAR-10/100，ImageNet-1K，（分割）ADE20K，（图片生成）FFHQ，（指令微调）Alpaca。训练的模型包括（分类）ResNet18，ResNet-50，ViT-Base(MAE)， Swin-Tiny，(分割)UperNet，(图片生成)Latent Diffusion, （指令微调）LLaMA-7B。

3.2 实验结果

这里展示主要结果，更多结果请参考论文。

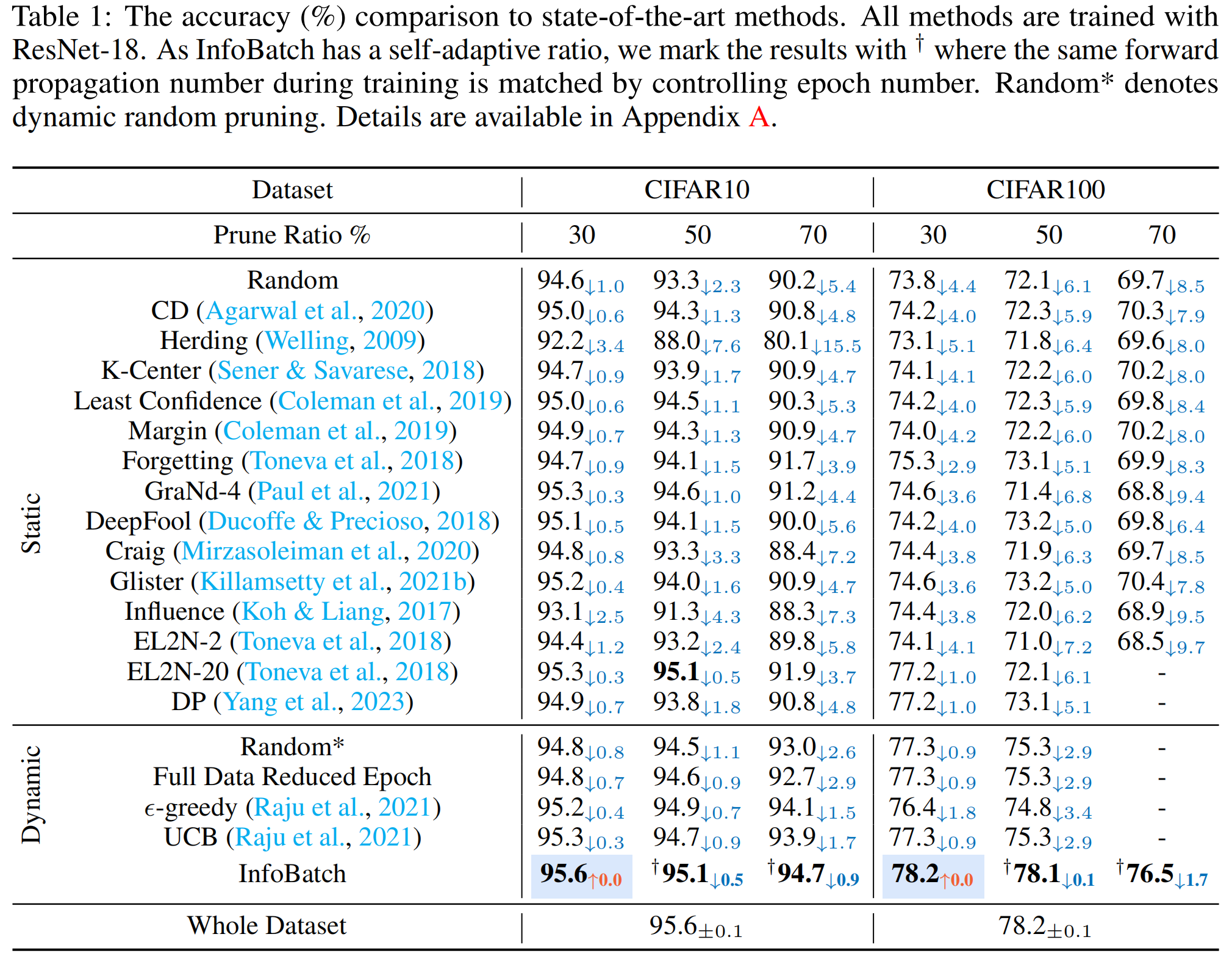
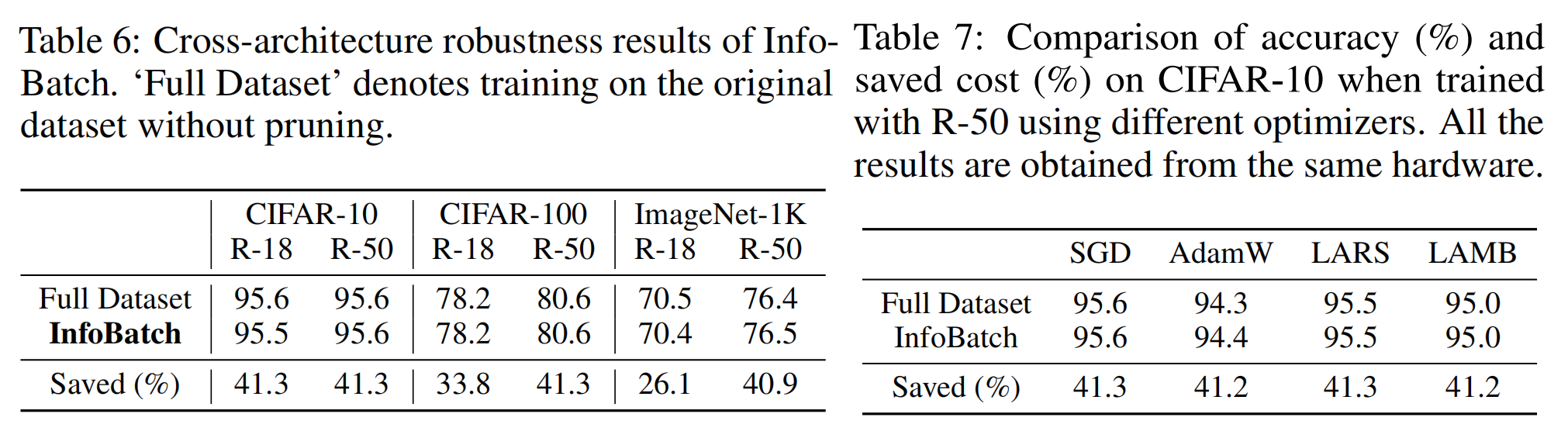
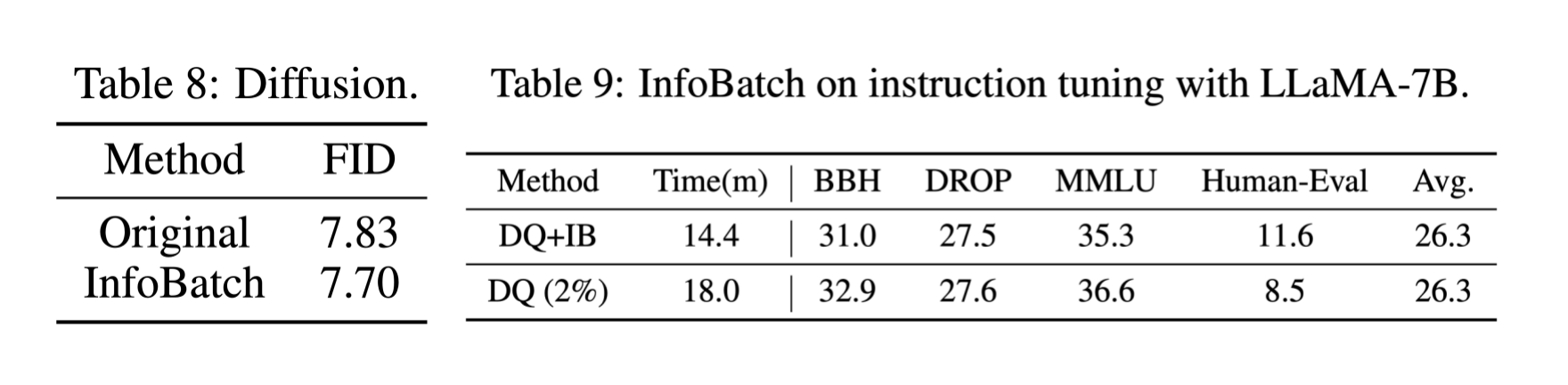
另外，根据作者最新更新，InfoBatch在检测任务上也取得了无损加速30%的效果，代码将会在github更新。

四、总结与展望

在这项工作中，作者提出了InfoBatch框架，能够在广泛的任务上可观地节省训练开销并加速。其核心的思想是根据样本拟合情况动态调整采样剪枝策略，并利用重缩放维持更新量的一致。作者在文中进一步探讨了该策略的适用范围和进一步的优化，期待此类工作以后能取代传统数据迭代方式，助力大模型时代训练加速。

参考

[1]Zhao, Bo, and Hakan Bilen. “Dataset condensation with distribution matching.” Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision. 2023.

[2]Har-Peled, Sariel, and Soham Mazumdar. “On coresets for k-means and k-median clustering.” Proceedings of the thirty-sixth annual ACM symposium on Theory of computing. 2004.

[3]Csiba, Dominik, and Peter Richtárik. “Importance sampling for minibatches.” The Journal of Machine Learning Research 19.1 (2018): 962-982.