模拟退火算法（SA）解决旅行商(TSP)问题的python实现

旅行商问题

旅行商问题（Travelling Salesman Problem, 简记TSP，亦称货郎担问题)：设有n个城市和距离矩阵D = [dij]，其中dij表示城市i到城市j的距离，i, j = 1, 2 … n，则问题是要找出遍访每个城市恰好一次的一条回路并使其路径长度为最短。
说明： 回路：从某个城市出发，最后回到这个城市。

模拟退火算法

模拟退火算法（Simulated Annealing）是一种启发式优化算法，受到固体退火过程的启发。该算法通过模拟物质在高温下退火冷却的过程，从而在解空间中跳出局部最优解，寻找全局最优解。
简单来说，模拟退火算法的主要步骤包括：
1 初始化：随机选择一个初始解，并设定初始温度（Temperature）。
2 **循环迭代：**在当前解的基础上进行微小的扰动，生成一个新解。计算新解的目标函数值（或者称为能量值）和当前解的目标函数值的差异（ΔE）。如果 ΔE 小于0，即新解更优，接受新解。如果 ΔE 大于0，以一定的概率（由一个概率分布计算得出，通常是玻尔兹曼分布）接受新解。这个概率随着温度的降低而减小，但在开始时有较大的概率接受劣解，以便跳出局部最优解。
3 降低温度，通常按照某个固定的降温率进行。
4 终止条件：当温度降低到足够低（接近零）或者达到最大迭代次数时停止算法。最终的解即为所求解。
这种随机性和“接受劣解”的策略使得模拟退火算法有可能避免陷入局部最优解，同时在搜索空间中进行广泛的探索，从而找到更优的解。算法中的温度和接受劣解的概率是关键的参数，它们影响了算法的探索性能。

在TSP问题中，模拟退火算法在解决旅行商问题（TSP）时的思路是通过在解空间中进行随机游走，模拟“退火”过程中的分子在热系统中的运动。具体步骤如下：
1 初始化解：随机生成一个初始路径，表示旅行商依次访问城市的顺序。
2 设定初始温度：初始时，系统的“温度”很高，容许接受较差的解。初始温度的选择对算法的性能有影响，通常由问题的特性和经验决定。
3 迭代过程：在当前解的基础上进行微小的扰动，例如交换两个城市的顺序，得到一个新的解。计算新解的路径长度与当前解的路径长度之差（ΔE）。如果 ΔE 小于0，即新解更优，直接接受新解。如果 ΔE 大于0，以一定的概率（由温度和 ΔE 决定）接受新解。温度高时，概率较大，有较大可能性接受劣解；随着迭代进行，温度逐渐降低，接受劣解的概率减小，算法越来越趋向于选择更好的解。
4 降低温度：在每个迭代步骤后，通过一个降温策略减小温度。典型的降温策略是乘以一个小于1的因子。
5 终止条件：当温度降低到足够低（接近零）或者达到最大迭代次数时停止算法。此时，当前解即为所求解。

代码实现

import random
import math

# 读取 .tsp 文件以获取元数据
def read_tsp_file(filename):
    metadata = {}
    with open(filename, 'r') as file:
        lines = file.readlines()
        for line in lines:
            if line.startswith("DIMENSION"):
                metadata["num_cities"] = int(line.split(":")[1])
            # 可以根据需要解析其他元数据
            
    return metadata

# 读取距离矩阵文件 .d
def read_distance_matrix(filename, num_cities):
    with open(filename, 'r') as file:
        lines = file.readlines()
    
    # 解析距离矩阵
    distance_matrix = []
    for line in lines:
        row = [int(dist) for dist in line.strip().split()]
        distance_matrix.append(row)
    
    return distance_matrix

# 计算路径长度
def calculate_path_length(path, distance_matrix):
    total_distance = 0
    for i in range(len(path) - 1):
        total_distance += distance_matrix[path[i]][path[i + 1]]
    total_distance += distance_matrix[path[-1]][path[0]]  # 回到起始城市
    return total_distance


# 模拟退火算法
def simulated_annealing(distance_matrix, initial_temperature, cooling_rate, num_iterations):
    current_solution = random.sample(range(len(distance_matrix)), len(distance_matrix))
    current_energy = calculate_path_length(current_solution, distance_matrix)
    best_solution = current_solution
    best_energy = current_energy
    temperature = initial_temperature

    for _ in range(num_iterations):
        # 生成新解
        new_solution = current_solution[:]
        # 随机选择两个位置交换
        i, j = random.sample(range(len(new_solution)), 2)
        new_solution[i], new_solution[j] = new_solution[j], new_solution[i]
        new_energy = calculate_path_length(new_solution, distance_matrix)

        # 计算能量差
        delta_energy = new_energy - current_energy

        # 如果新解更优，或者以一定概率接受劣解
        if delta_energy < 0 or random.random() < math.exp(-delta_energy / temperature):
            current_solution = new_solution
            current_energy = new_energy

            # 更新最优解
            if current_energy < best_energy:
                best_solution = current_solution
                best_energy = current_energy

        # 降低温度
        temperature *= (1 - cooling_rate)

    return best_solution, best_energy



if __name__ == "__main__":
    tsp_metadata = read_tsp_file("dantzig42.tsp")
    initial_temperature = 1000  # 初始温度
    cooling_rate = 0.003  # 冷却率
    num_iterations = 1000000

    distance_matrix = read_distance_matrix("dantzig42_d.txt", tsp_metadata["num_cities"])
    '''
    # 创建自己的距离矩阵的实现 
    num_cities = 5
    distance_matrix = np.array([
    [0, 10, 20, 15, 30],   # 城市0到其他城市的距离
    [10, 0, 25, 20, 35],   # 城市1到其他城市的距离
    [20, 25, 0, 12, 28],   # 城市2到其他城市的距离
    [15, 20, 12, 0, 22],   # 城市3到其他城市的距离
    [30, 35, 28, 22, 0]    # 城市4到其他城市的距离
])
    
   '''

    best_path, best_distance = simulated_annealing(distance_matrix, initial_temperature, cooling_rate, num_iterations)

    print("最短路径:", best_path)
    print("最短距离:", best_distance)

结果展示

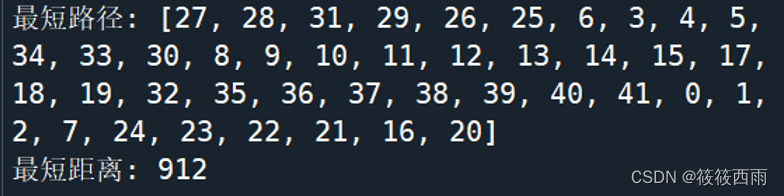
结果分析:

模拟退火算法（Simulated Annealing）是一种启发式优化算法，受到固体退火过程的启发。该算法通过模拟物质在高温下退火冷却的过程，从而在解空间中跳出局部最优解，寻找全局最优解。在模拟退火算法中，由于接受劣解的概率，每次运行的结果可能会有所不同。这种随机性是模拟退火算法的一个特点，它使得算法有可能跳出局部最优解，寻找到全局最优解
由于每次选择接受劣解的概率是基于当前的温度和新解与当前解的能量差异计算的，因此在不同的运行中，随机性会导致算法在搜索空间中不同的路径上进行探索。当温度较高时，算法更容易接受劣解，随着温度的逐渐降低，接受劣解的概率也逐渐降低，算法会越来越倾向于选择更好的解。可以增加模拟退火算法的迭代次数（num_iterations）以增加搜索空间中的探索，也可以调整初始温度（initial_temperature）和冷却率（cooling_rate）以影响算法的收敛速度。增加迭代次数和调整参数可能会增加算法的计算时间，但也会提高找到更优解的机会。所以每次的最短路径和最短距离可能不一样。