神经网络学习日记（三）——CNN卷积神经网络

本文是笔者为了完成毕业设计而进行学习的一个个人学习日记

图片和链接均源自网络，侵删

CNN网络结构

一个标准的卷积神经网络，通常由输入层、卷积层（Convolution layer)、激活层、池化层（Pooling layer）、全连接层、输出层构成。其中，卷积层、激活层和池化层一般会交替设置若干个，最后将数据传入到一个全连接层处理后输出。如下图：

其中，输入层、激活层、输出层已经进行过介绍，不再赘述，下面将主要介绍卷积层、池化层和全连接层。

CNN笔记：通俗理解卷积神经网络：https://blog.csdn.net/v_JULY_v/article/details/51812459

卷积神经网络（CNN）详细介绍及其原理详解：https://blog.csdn.net/IronmanJay/article/details/128689946

学习笔记：深度学习（3）——卷积神经网络（CNN）理论篇：https://blog.csdn.net/Morganfs/article/details/124121625

卷积层

卷积（Convolution） 的目的是从输入矩阵中提取数据，通过计算后得到指定特征（Features）。而用于提取数据并进行计算的工具叫做卷积核（Convolution Kernel），也叫滤波器（Filter）。

卷积核

卷积核本质上就是一组由固定权重组成的矩阵，输入数据会与卷积核做内积（各个位置的权重相乘后相加），得到特征值，如下图所示，中间$3\times 3$的矩阵就是卷积核：

而对于整个图像，卷积核会从左往右、从上往下地以一个或指定个像素的间距依次滑过图像的每一个区域，如下图：

假设$x$表示输入数据的二维矩阵，$w$表示卷积核二维矩阵，而$y$表示输出的特征矩阵，那么有：
$$y[i,j]=\sum _{u,v}x[i+u,j+v]?w[u,v]$$
当然，卷积核的大小并非固定为$3\times 3$，可以根据需要来调节大小（一般为奇数，因为我们通常希望卷积核有一个中心，便于处理输出）。然而，在进行计算时，我们可以发现，输入矩阵的边缘只被计算了一次，而中间位置却被计算了两次或多次，这样会导致得到的特征矩阵丢失边缘特征，最终导致特征提取不准确。为了解决这个问题，我们通常会采用填充和改变步长来解决。

填充/步长

• 填充（Pedding） 是指在输入矩阵的边缘填充数据（通常是0元素），从而调整输出的尺寸，同时，也可以减少卷积操作导致的边缘信息丢失。一般Pedding取值为1，当然也可以取值其他值。

• 步长（Stride） 是指卷积核每次滑动的像素数量，我们前面默认卷积核每次滑动一个像素，但在不同的卷积核大小情况下，也可以每次滑动2个或多个像素。若希望输出尺寸比输入尺寸小很多，可以采取增大步幅的措施。但是不能频繁使用步长为2，因为如果输出尺寸变得过小的话，即使卷积核参数优化的再好，也会不可避免地丢失大量信息.

设输入矩阵大小为$w$，卷积核大小为$k$，步长为$s$，填充层数为$p$，则卷积后产生的特征图大小计算公式为：
$$w^{\prime }=\frac{w+2p?k}{s}+1$$

下面两张图分别是Pedding取值为1（左）和Stride取值为2（右）时的卷积过程：

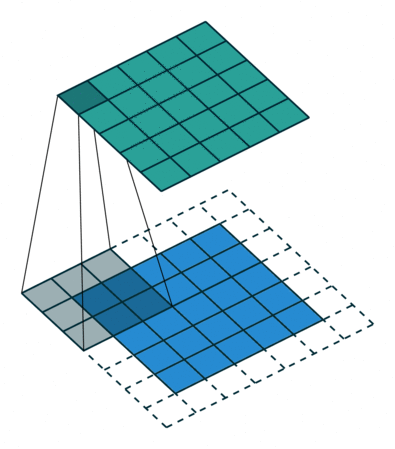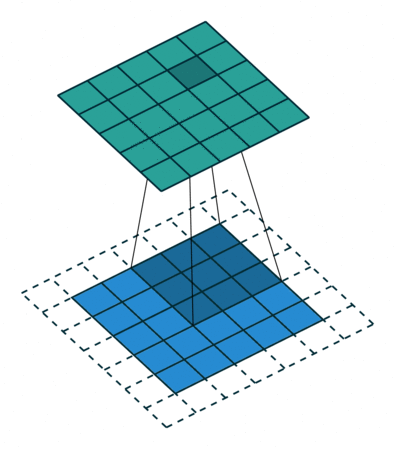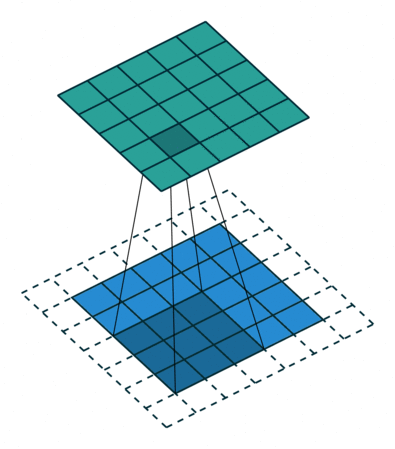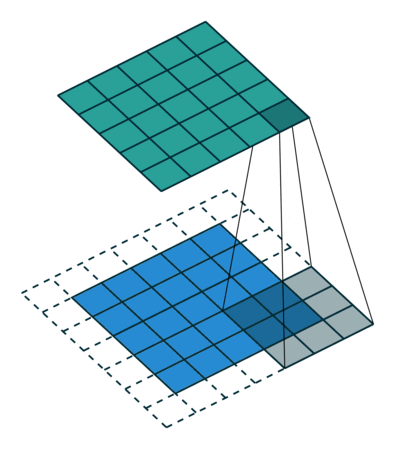
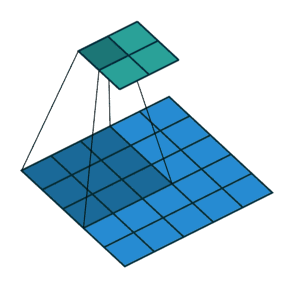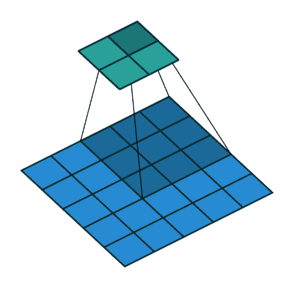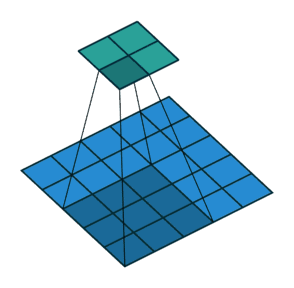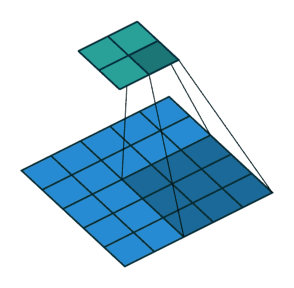
以上就是关于卷积层的一些相关知识，下面我们来了解一下池化层。

多卷积核

有时候，输入的情况比较复杂，一个卷积核可能没法很好地提取所有特征，那么我们也可以使用多卷积核。例如，一张彩色图片通常有三个通道（RGB），也就是三个二维矩阵，此时我们使用两组卷积核，即$2\times 3=6$个权重矩阵（假设大小为$3\times 3$）。对于一个卷积核，三个通道卷积出的数值之和，将作为该组卷积核的输出，因此两组卷积核将输出两个特征矩阵。如下动图所示，该图展示了一个通道数为3，输入矩阵大小为5，填充为1，步长为2，卷积核大小为3，共2组卷积核的卷积过程：

可以注意到，每组卷积核的下方有一个偏置值$b$，该偏置与FCNN相同，在一组卷积核运算完成后将加上这个偏置值。对于这样一个卷积过程，我们假设第$m$组第$n$个卷积核$w_{mn}$的输出结果为$y_{mn}$，它所对应的输入矩阵为$x_n$那么我们有：
$$y_{mn}[i,j]=\sum _{u,v}{x}_n[i+u,j+v]?w_{mn}[u,v]$$
对于该组的输出矩阵$o_m$我们有：
$$o_m[i,j]=\sum _n{y}_{mn}[i,j]+b_m$$
以上就是多卷积核的卷积流程。

池化层

通过上面对于卷积层的介绍，我们可以总结出一个事实，即：有几个卷积核就有多少个特征矩阵。现实中情况肯定更为复杂，也就会有更多的卷积核，那么就会有更多的特征矩阵。而过多的特征矩阵通常会带来下面两个问题：模型过拟合和维度过高。

因此，需要引入池化（Pooling） 来对特征矩阵进行下采样（Down-sample），即将得到的特征矩阵进行特征提取，将其中最具有代表性的特征提取出来，可以起到减小过拟合和降低维度的作用。例如，下图是一个简单的最大池化的例子：

常用的池化函数有：平均池化（Average Pooling / Mean Pooling）、最大池化（Max Pooling）、最小池化（Min Pooling） 和 随机池化（Stochastic Pooling） 等。由于要提取的是最具有代表性的特征，因此最小池化通常不太会用到，而另外3种池化方式展示如下：

三种池化方式各有优缺点：

• 平均池化可以减少邻域大小受限造成的估计值方差，但更多保留的是图像背景信息，另外，需要注意计算平均池化时采用向上取整；

• 最大池化能减少卷积层参数误差造成估计均值误差的偏移，能更多的保留纹理信息；

• 随机池化会通过对像素点按数值大小赋予概率，再按照概率进行亚采样，在平均意义上，与均值采样近似，在局部意义上，则服从最大值采样的准则，虽然可以保留均值池化的信息，但是随机概率值确是人为添加的。

我们注意到，池化的过程与卷积有些类似，也有一个类似卷积核的东西在特征矩阵上移动，我们称它为池化窗口。这个池化窗口也有大小、步长，池化前也可以有填充操作，一般来说，池化窗口的大小和步长会设定相同的值（如上图就是2）。

但是与卷积层不同的是，池化层没有要学习的参数，卷积层需要通过计算，因此卷积核有自身的权重值需要通过神经网络的学习来进行反向推导，而池化只是从池化窗口中取最大值或者平均值，因此没有学习的参数。

全连接层

在进行多次“卷积-激活-池化”的过程之后，我们可以得到关于初始输入数据的多个特征矩阵，此时我们需要将这些特征数据与最后输出的预测结果相关联起来，我们使用的是全连接层。

全连接层的结构在全连接神经网络一章已经详细介绍过了。显然，全连接层使用的是一维数据，因此，我们需要将我们提取的所有特征矩阵“展平”成$1\times x$的数据供其输入，例如，在经过一系列操作后，我们得到了如下特征矩阵：

将所有特征矩阵“展平”：

此时，所有特征矩阵构成了一个一维的“输入层”，我们只需要构建一个输入层为该一维数据，输出层为我们需要的分类数据的FCNN：

最后根据训练好的数据，得到该特征输入的即，整个CNN的流程如下图所示：

[透析] 卷积神经网络CNN究竟是怎样一步一步工作的？：https://www.jianshu.com/p/fe428f0b32c1

个人神经网络学习日记：
神经网络学习日记（一）——神经网络基本概念
神经网络学习日记（二）——全连接神经网络及Pytorch代码实现
神经网络学习日记（三）——CNN卷积神经网络
神经网络学习日记（四）——RNN、LSTM、BiLSTM、GRU
神经网络学习日记（五）——数据加载器（DataLoader）的调用

由于是第一次写博客，不知道是否有侵犯其他人文章版权的问题，如果有请务必联系我，谢谢！