DBSCAN聚类模型

发布时间：2024年01月07日

介绍：?

一、数据?

?二、建模

三、评价指标?

3.1metrics.homogeneity_score

3.2metrics.completeness_score

3.3metrics.v_measure_score

3.4metrics.adjusted_rand_score

3.5metrics.adjusted_mutual_info_score

3.6metrics.silhouette_score

四、画图

4.1团簇

4.2圈图

介绍：?

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一种基于密度的聚类算法。它能够将具有足够高密度的数据点聚类在一起，并且能够识别噪声点。

DBSCAN算法的基本思想是通过计算每个数据点的邻域密度来确定聚类。具体而言，算法从一个未访问的数据点开始，找到其邻域内的所有数据点。如果邻域内包含足够数量的数据点，则形成一个聚类。然后，对于聚类中的每个数据点，继续查找其邻域内的数据点，并将其加入到聚类中。这个过程不断重复，直到所有的数据点都被访问过。

DBSCAN算法的特点是能够识别任意形状的聚类，并且对噪声点具有鲁棒性。它不需要预先指定聚类的个数，也不受聚类的形状和大小限制。此外，DBSCAN算法还能够处理具有不同密度的数据。

DBSCAN算法的主要参数是邻域半径(epsilon)和最小邻域数(minPts)。邻域半径和最小邻域数决定了聚类的紧密度和噪声点的容忍度。通过调整这两个参数，可以得到不同的聚类结果。

总而言之，DBSCAN算法是一种强大的聚类算法，适用于多种数据集和应用场景。它能够根据数据点的密度特征自动确定聚类，并且能够处理噪声点。

一、数据?

#DBSCAN with cluster spherical data

import numpy as np
from sklearn.cluster import DBSCAN
from sklearn import metrics
from sklearn.datasets import make_blobs
from sklearn.preprocessing import StandardScaler

# Generate sample data
centers = [[1, 1], [-1, -1], [1, -1]]#团状的坐标中心
X, labels_true = make_blobs(n_samples=750, centers=centers, cluster_std=0.4,
                            random_state=0)

##n_samples：生成的样本点的总数。
##n_features：生成的样本点的特征数。
##centers：要生成的样本点的中心数或固定中心的位置。
##cluster_std：每个类别的标准差。
##center_box：中心点的箱子边界。
##shuffle：是否打乱样本点的顺序。
##random_state：随机数生成器的种子。

X.shape
#（750，2）

labels_true
'''结果：
array([0, 1, 0, 2, 0, 1, 1, 2, 0, 0, 1, 1, 1, 2, 1, 0, 1, 1, 2, 2, 2, 2,
       2, 2, 1, 1, 2, 0, 0, 2, 0, 1, 1, 0, 1, 0, 2, 0, 0, 2, 2, 1, 1, 1,
       1, 1, 0, 2, 0, 1, 2, 2, 1, 1, 2, 2, 1, 0, 2, 1, 2, 2, 2, 2, 2, 0,
       2, 2, 0, 0, 0, 2, 0, 0, 2, 1, 0, 1, 0, 2, 1, 1, 0, 0, 0, 0, 1, 2,
       1, 2, 2, 0, 1, 0, 1, 0, 1, 1, 0, 0, 2, 1, 2, 0, 2, 2, 2, 2, 0, 0,
       0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 2, 1, 0, 0, 1, 2, 1, 0, 0, 2, 0, 2,
       2, 2, 0, 1, 2, 2, 0, 1, 0, 2, 0, 0, 2, 2, 2, 2, 1, 0, 2, 1, 1, 2,
       2, 2, 0, 1, 0, 1, 0, 1, 0, 2, 2, 1, 1, 2, 2, 1, 0, 1, 2, 2, 2, 1,
       1, 2, 2, 0, 1, 2, 0, 0, 2, 0, 0, 1, 0, 1, 0, 1, 1, 2, 2, 0, 0, 1,
       1, 2, 1, 2, 2, 2, 2, 0, 2, 0, 2, 2, 0, 2, 2, 2, 0, 0, 1, 1, 1, 2,
       2, 2, 2, 1, 2, 2, 0, 0, 2, 0, 0, 0, 1, 0, 1, 1, 1, 2, 1, 1, 0, 1,
       2, 2, 1, 2, 2, 1, 0, 0, 1, 1, 1, 0, 1, 0, 2, 0, 2, 0, 2, 2, 2, 1,
       1, 0, 0, 1, 1, 0, 0, 2, 1, 2, 2, 1, 1, 2, 1, 2, 0, 2, 2, 0, 1, 2,
       2, 0, 2, 2, 0, 0, 2, 0, 2, 0, 2, 1, 0, 0, 0, 1, 2, 1, 2, 2, 0, 2,
       2, 0, 0, 2, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 2, 0,
       1, 2, 2, 0, 0, 2, 0, 2, 1, 0, 2, 0, 2, 0, 2, 2, 0, 1, 0, 1, 0, 2,
       2, 1, 1, 1, 2, 0, 2, 0, 2, 1, 2, 2, 0, 1, 0, 1, 0, 0, 0, 0, 2, 0,
       2, 0, 1, 0, 1, 2, 1, 1, 1, 0, 1, 1, 0, 2, 1, 0, 2, 2, 1, 1, 2, 2,
       2, 1, 2, 1, 2, 0, 2, 1, 2, 1, 0, 1, 0, 1, 1, 0, 1, 2, 0, 1, 0, 0,
       2, 1, 2, 2, 2, 2, 1, 0, 0, 0, 0, 1, 0, 2, 1, 0, 1, 2, 0, 0, 1, 0,
       1, 1, 0, 2, 0, 2, 2, 2, 1, 1, 2, 0, 1, 0, 0, 1, 0, 1, 1, 2, 2, 1,
       0, 1, 2, 2, 1, 1, 1, 1, 0, 0, 0, 2, 2, 1, 2, 1, 0, 0, 1, 2, 1, 0,
       0, 2, 0, 1, 0, 2, 1, 0, 2, 2, 1, 0, 2, 0, 2, 1, 1, 0, 2, 0, 0, 1,
       1, 1, 1, 0, 1, 0, 1, 0, 0, 2, 0, 1, 1, 2, 1, 1, 0, 1, 0, 2, 1, 0,
       0, 1, 0, 1, 1, 2, 2, 1, 2, 2, 1, 2, 1, 1, 1, 1, 2, 0, 0, 0, 1, 2,
       2, 0, 2, 0, 2, 1, 0, 1, 1, 0, 0, 1, 2, 1, 2, 2, 0, 2, 1, 1, 1, 2,
       0, 0, 2, 0, 2, 2, 0, 2, 0, 1, 1, 1, 1, 0, 0, 0, 2, 1, 1, 1, 1, 2,
       2, 2, 0, 2, 1, 1, 0, 0, 1, 0, 2, 1, 2, 1, 0, 2, 2, 0, 0, 1, 0, 0,
       2, 0, 0, 0, 2, 0, 2, 0, 0, 1, 1, 0, 0, 1, 2, 2, 0, 0, 0, 0, 2, 1,
       1, 1, 2, 1, 0, 0, 2, 2, 0, 1, 2, 0, 1, 2, 2, 1, 0, 0, 0, 1, 2, 0,
       0, 0, 2, 2, 2, 0, 1, 1, 1, 1, 1, 0, 0, 2, 1, 2, 0, 1, 1, 1, 0, 2,
       1, 1, 1, 2, 1, 2, 0, 2, 2, 1, 0, 0, 0, 1, 1, 2, 0, 0, 2, 2, 1, 2,
       2, 2, 0, 2, 1, 2, 1, 1, 1, 2, 0, 2, 0, 2, 2, 0, 0, 2, 1, 2, 0, 2,
       0, 0, 0, 1, 0, 2, 1, 2, 0, 1, 0, 0, 2, 0, 2, 1, 1, 2, 1, 0, 1, 2,
       1, 2])
'''

?二、建模

X = StandardScaler().fit_transform(X)#标准化

# Compute DBSCAN 建模
db = DBSCAN(eps=0.3, min_samples=10).fit(X)

##DBSCAN函数有以下参数：
## `eps`：用来定义邻域的半径，超过这个半径的点会被认为是噪音点。默认值为0.5。
##`min_samples`：用来定义一个核心点的最小邻域样本数，如果某个点的邻域内的样本数小于这个值，则该点将被视为噪音点。默认值为5。
##`metric`：用来计算点与点之间的距离的方法。默认值为欧式距离。
## `algorithm`：用来指定计算最近邻的算法。可以选择"auto"（根据数据自动选择算法）、"ball_tree"、"kd_tree"或"brute"。默认值为"auto"。
## `leaf_size`：如果使用"ball_tree"或"kd_tree"算法，该参数用来指定叶子节点的大小。默认值为30。
## `p`：当使用Minkowski距离时，该参数用来指定距离的幂。默认值为2，即欧式距离。
## `n_jobs`：用来指定并行计算的数量。默认值为1，表示不进行并行计算。
## `eps_mode`：用来控制邻域半径的计算方式。可以选择"fixed"（固定的eps值）或"auto"（根据数据自动计算eps值）。默认值为"fixed"。
##以上是DBSCAN函数的一些常用参数，具体使用哪些参数需要根据具体的需求和数据情况来决定。

core_samples_mask = np.zeros_like(db.labels_, dtype=bool)

core_samples_mask[db.core_sample_indices_] = True
labels = db.labels_
'''结果：
array([ 0,  1,  0,  2,  0,  1,  1,  2,  0,  0,  1,  1,  1,  2,  1,  0, -1,
        1,  1,  2,  2,  2,  2,  2,  1,  1,  2,  0,  0,  2,  0,  1,  1,  0,
        1,  0,  2,  0,  0,  2,  2,  1,  1,  1,  1,  1,  0,  2,  0,  1,  2,
        2,  1,  1,  2,  2,  1,  0,  2,  1,  2,  2,  2,  2,  2,  0,  2,  2,
        0,  0,  0,  2,  0,  0,  2,  1, -1,  1,  0,  2,  1,  1,  0,  0,  0,
        0,  1,  2,  1,  2,  2,  0,  1,  0,  1, -1,  1,  1,  0,  0,  2,  1,
        2,  0,  2,  2,  2,  2, -1,  0, -1,  1,  1,  1,  1,  0,  0,  1,  0,
        1,  2,  1,  0,  0,  1,  2,  1,  0,  0,  2,  0,  2,  2,  2,  0, -1,
        2,  2,  0,  1,  0,  2,  0,  0,  2,  2, -1,  2,  1, -1,  2,  1,  1,
        2,  2,  2,  0,  1,  0,  1,  0,  1,  0,  2,  2, -1,  1,  2,  2,  1,
        0,  1,  2,  2,  2,  1,  1,  2,  2,  0,  1,  2,  0,  0,  2,  0,  0,
        1,  0,  1,  0,  1,  1,  2,  2,  0,  0,  1,  1,  2,  1,  2,  2,  2,
        2,  0,  2,  0,  2,  2,  0,  2,  2,  2,  0,  0,  1,  1,  1,  2,  2,
        2,  2,  1,  2,  2,  0,  0,  2,  0,  0,  0,  1,  0,  1,  1,  1,  2,
        1,  1,  0,  1,  2,  2,  1,  2,  2,  1,  0,  0,  1,  1,  1,  0,  1,
        0,  2,  0,  2,  2,  2,  2,  2,  1,  1,  0,  0,  1,  1,  0,  0,  2,
        1, -1,  2,  1,  1,  2,  1,  2,  0,  2,  2,  0,  1,  2,  2,  0,  2,
        2,  0,  0,  2,  0,  2,  0,  2,  1,  0,  0,  0,  1,  2,  1,  2,  2,
        0,  2,  2,  0,  0,  2,  1,  1,  1,  1,  1,  0,  1,  1,  1,  1,  0,
        0,  1,  1,  1,  0,  2,  0,  1,  2,  2,  0,  0,  2,  0,  2,  1,  0,
        2,  0,  2,  0,  2,  2,  0,  1,  0,  1,  0,  2,  2,  1,  1,  1,  2,
        0,  2,  0,  2,  1,  2,  2,  0,  1,  0,  1,  0,  0,  0,  0,  2,  0,
        2,  0,  1,  0,  1,  2,  1,  1,  1,  0,  1,  1,  0,  2,  1,  0,  2,
        2,  1,  1,  2,  2,  2,  1,  2,  1,  2,  0,  2,  1,  2,  1,  0,  1,
        0,  1,  1,  0,  1,  2, -1,  1,  0,  0,  2,  1,  2,  2,  2,  2,  1,
        0,  0,  0,  0,  1,  0,  2,  1,  0,  1,  2,  0,  0,  1,  0,  1,  1,
        0, -1,  0,  2,  2,  2,  1,  1,  2,  0,  1,  0,  0,  1,  0,  1,  1,
        2,  2, -1,  0,  1,  2,  2,  1,  1,  1,  1,  0,  0,  0,  2,  2,  1,
        2,  1,  0,  0,  1,  2,  1,  0,  0,  2,  0,  1,  0,  2,  1,  0,  2,
        2,  1,  0,  0,  0,  2,  1,  1,  0,  2,  0,  0,  1,  1,  1,  1,  0,
        1,  0,  1,  0,  0,  2,  0,  1,  1,  2,  1,  1,  0,  1,  0,  2,  1,
        0,  0,  1,  0,  1,  1,  2,  2,  1,  2,  2,  1,  2,  1,  1,  1,  1,
        2,  0,  0,  0,  1,  2,  2,  0,  2,  0,  2,  1,  0,  1,  1,  0,  0,
        1,  2,  1,  2,  2,  0,  2,  1,  1,  1,  2,  0,  0,  2,  0,  2,  2,
        0,  2,  0,  1,  1,  1,  1,  0,  0,  0,  2,  1,  1,  1,  1,  2,  2,
        2,  0,  2,  1,  1,  0,  0,  1,  0,  2,  1,  2,  1,  0,  2,  2,  0,
        0,  1,  0,  0,  2,  0,  0,  0,  2,  0,  2,  0,  0,  1,  1,  0,  0,
        1,  2,  2,  0,  0,  0,  0,  2, -1,  1,  1,  2,  1,  0,  0,  2,  2,
        0,  1,  2,  0,  1,  2,  2,  1,  0,  0, -1, -1,  2,  0,  0,  0,  2,
       -1,  2,  0,  1,  1,  1,  1,  1,  0,  0,  2,  1,  2,  0,  1,  1,  1,
        0,  2,  1,  1, -1,  2,  1,  2,  0,  2,  2,  1,  0,  0,  0,  1,  1,
        2,  0,  0,  2,  2,  1,  2,  2,  2,  0,  2,  1,  2,  1,  1,  1,  2,
        0,  2,  0,  2,  2,  0,  0,  2,  1,  2,  0,  2,  0,  0,  0,  1,  0,
        2,  1,  2,  0,  1,  0,  0,  2,  0,  2,  1,  1,  2,  1,  0,  1,  2,
        1,  2], dtype=int64)
'''

三、评价指标?

3.1metrics.homogeneity_score

metrics.homogeneity_score是一个用于评估聚类结果的指标，它衡量了每个聚类都只包含同一个真实类别的程度。具体来说，homogeneity_score计算每个真实类别在被分配到的聚类中的比例，并对这些比例取平均值。如果聚类结果完全一致，所有的真实类别只包含在一个聚类中，homogeneity_score的值为1；如果聚类结果完全不一致，所有的真实类别均被分散到不同的聚类中，homogeneity_score的值为0。homogeneity_score的取值范围在0到1之间，数值越高表示聚类结果越好。

3.2metrics.completeness_score

metrics.completeness_score是一个用于度量聚类算法结果的完整性的指标。它衡量了聚类结果中每个类别所包含的样本数量与原始数据集中属于该类别的样本数量之比的平均值。具体计算方式如下：

completeness_score = 1 - H(C|K) / H(C)

其中，H(C|K)表示给定聚类结果K的条件熵，即在已知聚类结果K的条件下，真实类别C的熵。H(C)表示真实类别C的熵，即在不考虑聚类结果的情况下，真实类别C的熵。

completeness_score的取值范围在[0, 1]之间，越接近1表示聚类结果越完整，即每个类别中的样本都属于同一个真实类别。

3.3metrics.v_measure_score

metrics.v_measure_score是一种用于比较两个聚类结果相似性的评估指标。它结合了聚类结果的精确度（homogeneity）和完整度（completeness），通过计算调和平均值来得出最终的分数。精确度衡量的是同一类样本被分到同一簇的程度，完整度衡量的是同一簇的样本被分到同一类的程度。v_measure_score的取值范围在0和1之间，数值越大表示聚类结果越相似。

3.4metrics.adjusted_rand_score

metrics.adjusted_rand_score是一个评估聚类算法性能的指标。它用于比较聚类结果和真实标签之间的相似性。调整兰德指数（Adjusted Rand Index，ARI）是一种广泛使用的聚类评估指标之一。

调整兰德指数的取值范围从-1到1。当ARI的值接近1时，表示聚类结果与真实标签高度一致；当ARI的值接近0时，表示聚类结果与真实标签随机一致；而当ARI的值接近-1时，表示聚类结果与真实标签完全不一致。

该指标基于真实的分类标签和聚类算法产生的标签之间的匹配程度，并考虑到了随机聚类所产生的匹配情况。因此，调整兰德指数能够更准确地评估聚类算法的性能。

3.5metrics.adjusted_mutual_info_score

metrics.adjusted_mutual_info_score是一个用来度量聚类算法结果与真实标签之间的相似性的评价指标。聚类是一种无监督学习算法，它将数据点分成不同的组或簇。而真实标签表示每个数据点的真实类别。adjusted_mutual_info_score计算聚类结果与真实标签之间的调整后的互信息，用来评估聚类算法的性能。互信息是一种度量两个随机变量之间相互依赖程度的指标，而调整后的互信息是对互信息进行调整，以解决聚类数量不同时评价指标值的问题。通过比较不同聚类算法的adjusted_mutual_info_score，可以评估它们在数据集上的性能和效果。

3.6metrics.silhouette_score

metrics.silhouette_score是一个计算聚类模型的轮廓系数的函数。轮廓系数是一种用来评估聚类质量的指标，它衡量了每个样本距离其所属聚类的紧密程度和与其他聚类的分离程度。轮廓系数的取值范围是[-1, 1]，数值越接近1表示聚类效果越好。?

# Number of clusters in labels, ignoring noise if present.
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
n_noise_ = list(labels).count(-1)

n_clusters_#有三个团
#3

n_noise_#噪音个数
#18

print('Estimated number of clusters: %d' % n_clusters_)
print('Estimated number of noise points: %d' % n_noise_)
print("Homogeneity: %0.3f" % metrics.homogeneity_score(labels_true, labels))
print("Completeness: %0.3f" % metrics.completeness_score(labels_true, labels))
print("V-measure: %0.3f" % metrics.v_measure_score(labels_true, labels))
print("Adjusted Rand Index: %0.3f"
      % metrics.adjusted_rand_score(labels_true, labels))
print("Adjusted Mutual Information: %0.3f"
      % metrics.adjusted_mutual_info_score(labels_true, labels))
print("Silhouette Coefficient: %0.3f"
      % metrics.silhouette_score(X, labels))
'''结果：
Estimated number of clusters: 3
Estimated number of noise points: 18
Homogeneity: 0.953
Completeness: 0.883
V-measure: 0.917
Adjusted Rand Index: 0.952
Adjusted Mutual Information: 0.916
Silhouette Coefficient: 0.626
'''

四、画图

4.1团簇

# Plot result 画图
import matplotlib.pyplot as plt
%matplotlib inline

# Black removed and is used for noise instead.
unique_labels = set(labels)

unique_labels
#结果：{-1, 0, 1, 2}

colors = [plt.cm.Spectral(each)
          for each in np.linspace(0, 1, len(unique_labels))]
'''结果：
[(0.6196078431372549, 0.00392156862745098, 0.25882352941176473, 1.0),
 (0.9934640522875817, 0.7477124183006535, 0.4352941176470587, 1.0),
 (0.7477124183006538, 0.8980392156862746, 0.6274509803921569, 1.0),
 (0.3686274509803922, 0.30980392156862746, 0.6352941176470588, 1.0)]
'''

for k, col in zip(unique_labels, colors):
    if k == -1:
        # Black used for noise.
        col = [0, 0, 0, 1]

    class_member_mask = (labels == k)

    xy = X[class_member_mask & core_samples_mask]
    plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
             markeredgecolor='k', markersize=14)

    xy = X[class_member_mask & ~core_samples_mask]
    plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
             markeredgecolor='k', markersize=6)

plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()

4.2圈图

import numpy as np
import matplotlib.pyplot as plt
from sklearn import metrics
from sklearn.datasets import make_circles
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import DBSCAN

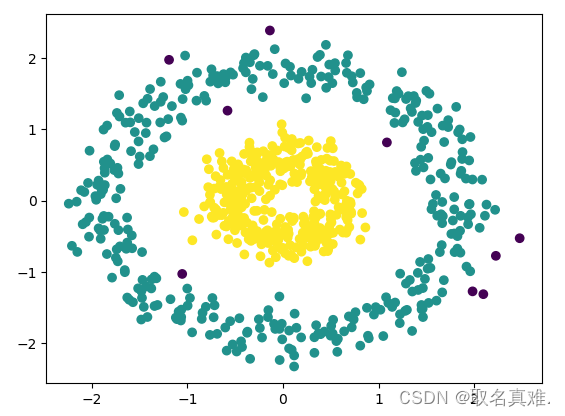
X, y = make_circles(n_samples=750, factor=0.3, noise=0.1)
X = StandardScaler().fit_transform(X)
y_pred = DBSCAN(eps=0.3, min_samples=10).fit_predict(X)

plt.scatter(X[:,0], X[:,1], c=y_pred)
print('Number of clusters: {}'.format(len(set(y_pred[np.where(y_pred != -1)]))))
print('Homogeneity: {}'.format(metrics.homogeneity_score(y, y_pred)))
print('Completeness: {}'.format(metrics.completeness_score(y, y_pred)))
print("V-measure: %0.3f" % metrics.v_measure_score(labels_true, labels))
print("Adjusted Rand Index: %0.3f"
      % metrics.adjusted_rand_score(labels_true, labels))
print("Adjusted Mutual Information: %0.3f"
      % metrics.adjusted_mutual_info_score(labels_true, labels))
print("Silhouette Coefficient: %0.3f"
      % metrics.silhouette_score(X, labels))


'''结果：
Number of clusters: 2
Homogeneity: 1.0
Completeness: 0.924494011741168
V-measure: 0.917
Adjusted Rand Index: 0.952
Adjusted Mutual Information: 0.916
Silhouette Coefficient: -0.074
'''

文章来源:https://blog.csdn.net/qq_74156152/article/details/135441207
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！