三次 Bezier 曲线 bern 基函数的形式
Bezier 曲线的控制多边形有 4 个控制点, P 0 P_0 P0?、 P 1 P_1 P1?、 P 2 P_2 P2? 和 P 3 P_3 P3?, Bezier 曲线是三次多项式,称为三次 Bezier 曲线,
P
(
t
)
=
∑
i
=
0
3
P
i
B
i
,
3
(
t
)
=
(
1
?
t
)
3
P
0
+
3
t
(
1
?
t
)
2
P
1
+
3
t
2
(
1
?
t
)
P
2
+
t
3
P
3
\begin{equation} P(t) = \sum_{i=0}^{3}P_i B_{i, 3}(t) = (1-t)^3 P_0 + 3t(1-t)^2P_{1} + 3t^2(1-t)P_2 + t^3P_3 \end{equation}
P(t)=i=0∑3?Pi?Bi,3?(t)=(1?t)3P0?+3t(1?t)2P1?+3t2(1?t)P2?+t3P3???
B
0
,
3
(
t
)
=
(
1
?
t
)
3
B
1
,
3
(
t
)
=
3
t
(
1
?
t
)
2
B
2
,
3
(
t
)
=
3
t
2
(
1
?
t
)
B
3
,
3
(
t
)
=
t
3
B_{0, 3}(t) = (1-t)^3 \\ B_{1, 3}(t) = 3t(1-t)^2 \\ B_{2, 3}(t) = 3t^2(1-t) \\ B_{3, 3}(t) = t^3
B0,3?(t)=(1?t)3B1,3?(t)=3t(1?t)2B2,3?(t)=3t2(1?t)B3,3?(t)=t3
double step = 0.01;
for (double t = 0.0; t < 1.0; t += step)
{
// 计算 基函数
p.x = 0;
p.y = 0;
double B03 = (1 - t) * (1 - t) * (1 - t);
double B13 = 3 * t * (1 - t) * (1 - t);
double B23 = 3 * t * t * (1 - t);
double B33 = t * t * t;
p.x += B03 * P[0].x + B13 * P[1].x + B23 * P[2].x + B33 * P[3].x;
p.y += B03 * P[0].y + B13 * P[1].y + B23 * P[2].y + B33 * P[3].y;
//pDC->LineTo(ROUND(p.x), ROUND(p.y));
}
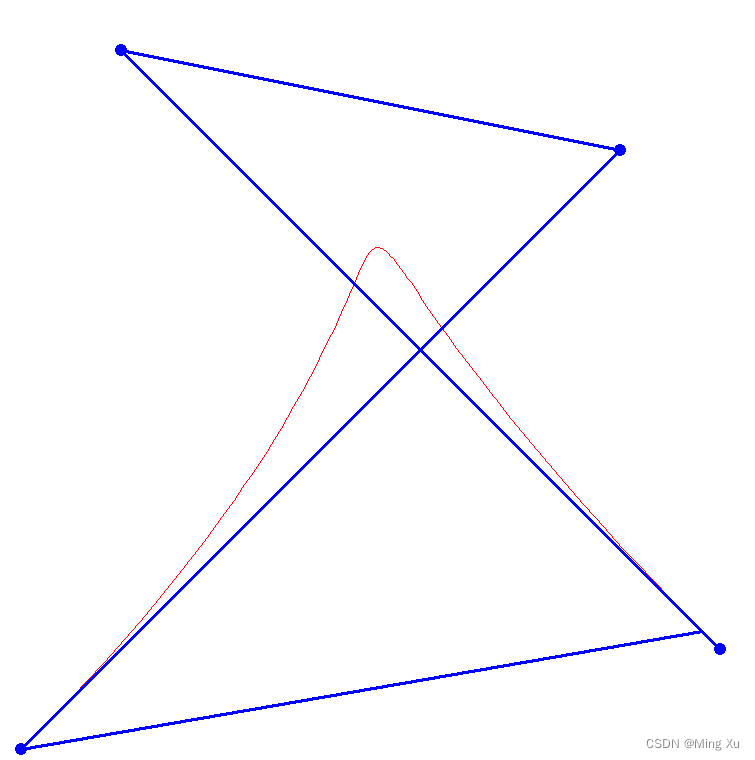
参考 《计算几何算法与实现》孔令德
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- STL之stack
- 无魔搭+ 函数计算: 一键部署,缩短大模型选型到生产的距离
- 浅了解一下『微前端』
- 小H靶场笔记:DC-7
- Springboot启动后自动退出解决办法
- Julia系列16:Julia与python/c互调
- 多维时序 | Matlab实现GRO-CNN-BiLSTM-Attention淘金算法优化卷积神经网络-双向长短期记忆网络结合注意力机制多变量时间序列预测
- Proxifier下载安装
- 办公自动应用,HR大屏可视化模板
- 4月阿里offer被毁,我是怎么进字节的?