DuNST详解：将Self-Training机制融入受控文本生成中

DuNST Dual Noisy Self Training for Semi-Supervised Controllable Text Generation

文章的主要工作

（1）第一个将自我训练纳入半监督可控语言生成中并提出一种新颖有效的ST方法的工作。
（2）证明 DuNST 探索了更大的潜在文本空间并扩展了泛化边界，为我们的方法提供了理论解释。
（3）对三个属性可控的生成任务进行了深入的实验，证明了 DuNST 在提高控制精度和生成文本的竞争质量方面的优越性，进一步扩展了强大的 PLM 用于 NLG 的能力。

---

DuNST方法

定义

让 $x$ 为文本，$y$ 为属性标签，$D_l=\{(x_i,y_i)\}$ 是一个带有配对文本及其相应标签的标记数据集， D u = { x i } D_u = \{ x_i \} Du?={xi?} 是来自同一领域的无标记数据集。我们的目标是学习一个由 $\theta$ 参数化的属性可控生成器 $G=g_{\theta }(x|y)$（例如，一个大型的PLM），以生成高质量的文本 $x～g_{\theta }(x|y)$（以自回归方式），满足给定的标签 $y$。我们还赋予我们的模型能力，通过联合学习一个文本分类器 $C=q_{?}(y|x)$ 为 $x\in D_u$ 生成伪属性标签。我们同时对 $G$ 和 $C$ 用一个共享的PLM作为双重过程来建模和优化（见第3.2节）。

在DuNST的训练过程中（见第3.3节），由 $C$ 预测的伪标签有助于覆盖更多未见样本，从而扩展了学习的分布边界，而由 $G$ 生成的噪声伪文本有助于扰动先前学习的空间，进一步提高泛化。

双重生成与分类

我们联合学习文本的条件分布 $g_{\theta }(x|y)$ 和标签 $q_{?}(y|x)$ 来匹配真实的分布。然而，我们并不直接使用传统的交叉熵损失函数来优化它们，而是采用变分方法。具体来说，我们引入了一个潜在变量 $z$ 来捕获底层语义，因此我们有 $q(x|y)=\int q(x,z|y)dz$。我们可以通过分解 $q(x,z|y)=q(x|z,y)?q(z|y)$ 来采样生成文本 $x$。为了实现这个目标，我们将生成损失最小化为：

$$L_g=?{\mathbb{E}}_{p_{\psi }(z|x,y)}[\log q_{\theta }(x|z,y)]+KL[p_{\psi }(z|x,y)||q_{\theta }(z|y)],\text{\hspace{1em}(1)}$$

其中 $p_{\psi }(z|x,y)$ 和 $q_{\theta }(z|y)$ 分别是 $z$ 的后验分布和先验分布的近似，KL 是指Kullback-Leibler散度。优化这个损失相当于最大化 $q_{\theta }(x|y)$ 的下界。

后验 $p_{\psi }(z|x,y)$ 通常假设为多元高斯分布 $N({\mu }_{post},{\sigma }_{post})$，并通过 $[{\mu }_{post},\log {\sigma }_{post}]=MLP([h_x,h_y])$ 近似，其中 $h_x=\text{Encoder}(x)$，$h_y$ 是标签 $y$ 的嵌入表示。编码器是Transformer编码器，MLP是多层感知机。同样，我们可以构建先验 $q_{\theta }(z|y)$ 为高斯分布 $N({\mu }_{gen}^{prior},{\sigma }_{gen}^{prior})$，其中 $[{\mu }_{gen}^{prior},\log {\sigma }_{gen}^{prior}]=MLP(h_y)$。对称地，我们通过以下方式优化分类：

$$L_c=?{\mathbb{E}}_{p_{\psi }(z|x,y)}[\log q_{?}(y|z,x)]+KL[p_{\psi }(z|x,y)||q_{?}(z|x)].\text{\hspace{1em}(2)}$$

文本是由自回归Transformer解码器生成的，$x=\text{Decoder}(z)$，标签是由 $y=MLP(z)$ 预测的，$z$ 在训练时从后验分布抽样，在测试时从先验分布抽样。$G$ 和 $C$ 大部分参数共享（例如，编码器），以及相同的后验分布 $p_{\psi }(z|x,y)$，以增强文本与相应标签的联系，并更好地利用通过这两个方向学到的知识。

最终的损失函数如下计算：

$$\mathcal{L}={\lambda }_g{L}_g+{\lambda }_c{L}_c,\text{\hspace{1em}(3)}$$

其中 ${\lambda }_g$ 和 ${\lambda }_c$ 是超参数，用于平衡分类与生成的重要性。这种变分双重学习进一步增强了可控性和文本多样性，并有助于精炼伪标签。

双重噪声自我训练

仅通过自生成文本增强的模型将越来越多地利用之前学到的空间，但失败于进行更多的探索，导致属性分布受限，因此控制精度的提升有限（见表1）。将噪声注入到伪文本中是促进探索的一种实践方式。然而，典型的合成噪声（例如，随机地在伪文本中洗牌令牌）鼓励各向同性探索，这可能会偏离有效空间，并且对于自然语言生成过于嘈杂。

为了解决这个问题，我们提出了两种新颖而有效的软噪声类型以实现更安全的探索，即高温生成和软伪文本。

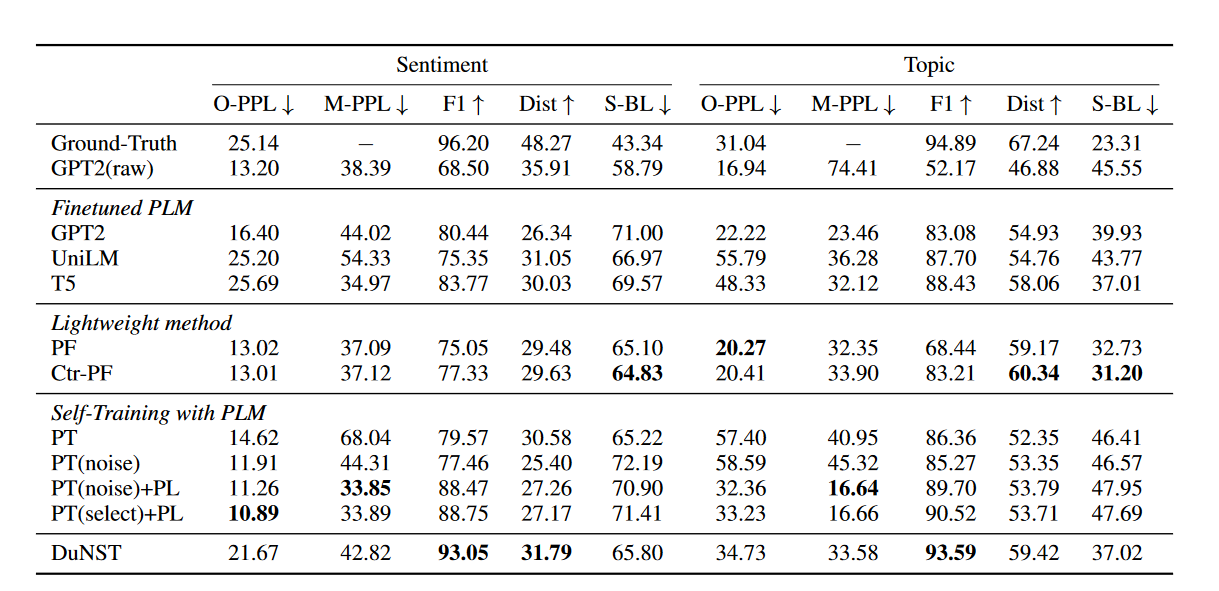
表 1：IMDb 数据集（情绪）和 AGNews 数据集（主题）的结果。

高温生成（HTG）：我们在softmax层引入温度 $\tau$：

$$d^m=\sigma (\frac{G(y,{\hat{x}}_{<m},z)}{\tau }),\text{\hspace{1em}(4)}$$

其中 $d^m$ 是第 $m$ 个令牌的输出分布，${\hat{x}}_{<m}$ 是之前生成的 $m?1$ 个令牌，$\sigma$ 表示softmax。较低的 $\tau$（例如，$\tau <1$）会导致更尖锐的分布，因此激励更确定的输出（通常用于NMT）。相反地，我们选择 $\tau >1$ 来鼓励更多样化但语义上合理的（高生成概率）令牌，这可以增强局部平滑性并帮助探索更多潜在方向。此外，通过调整 $\tau$ 可以轻松控制噪声程度以获得更好的权衡。

软伪文本（SPT）：HTG提高了伪文本的多样性，但也存在抽样无效令牌和在自回归生成中传播错误的风险。此外，HTG产生离散的伪文本（文本空间中的一个点），因此需要大量的抽样伪文本（点）来覆盖小区域（见图2）。因此，我们进一步提出生成软伪文本，其中我们直接存储输出令牌分布 $d$，并让 $G$ 直接学习重现 $d$。然后我们用以下公式替换公式(1)：

$$L_g^{\prime }=?\log q_{\theta }(x|z,y)+KL[p_{\psi }(z|x,y)||q_{\theta }(z|y)],x,y\in D_L,D_{PL}$$
$$=KL[d||q_{\theta }(x|z,y)]+KL[p_{\psi }(z|x,y)||q_{\theta }(z|y)],x,y\in D_{PT}.\text{\hspace{1em}(5)}$$

• $D_l$: 表示带标签的数据集（labeled dataset
• $D_{PL}$: 表示伪标签数据集（pseudo-labeled dataset）
• $D_{PT}$: 这可能指的是伪训练数据集（pseudo-training dataset）

损失函数 $L_g^{\prime }$ 被用于调整模型在这三种不同类型的数据上的表现。对于带标签的数据 $D_l$，模型直接学习匹配真实标签；对于伪标签数据 $D_{PL}$，模型可能会利用自身生成的标签来进一步训练；而对于伪训练数据 $D_{PT}$，模型可能会在更探索性或正则化的方式下训练，以提高其对于不确定性的处理能力。

这样的SPT充当了一种迭代方式的知识蒸馏。通过这种方式，我们避免了在 $d$ 中丢失相关的语义信息并减少了所需的样本，进一步扩展了泛化边界。

完整算法在算法1中描述。

1. 初始化训练:

   • 使用带标签的数据集 $D_L$ 对基模型 $G$ 和 $C$ 进行联合训练。
   • 优化公式(3)定义的损失函数。
   • 保存最好的模型作为 $G_0$ 和 $C_0$。

2. 循环训练:

   • 对于每个训练周期（epoch），从 1 循环到 MaxEpoch（最大周期数）。
   • 对于无标签数据集 $D_U$ 中的每个样本 $x_i$：
     • 使用上一周期的模型 $C_{\text{epoch}?1}$ 来预测其标签 ${\hat{y}}_i$。
   • 创建一个伪标签数据集 $D_{PL}$，包含无标签数据点 $x_i$ 和它们的伪标签 ${\hat{y}}_i$。

3. 生成软伪文本:

   • 对于属性集 $Y$ 中的每个属性 $y_j$：
     • 采样 $t$ 个先验 { z k } k = 1 t \{z_k\}_{k=1}^t {zk?}k=1t?，遵循 $q_{\theta }(z|y_j)$ 分布。
     • 对于每个采样的 $z_k$：
       • 计算最长为 MaxLength 的软伪令牌分布 $d_k^m$，使用模型 $G_{\text{epoch}?1}$ 和公式(4)。
       • 将 $y_k$ 设置为 $y_j$，建立与 $d_k^m$ 相关联的标签。
   • 创建一个软伪文本数据集 $D_{PT}$，包含软伪令牌分布 $d_k$ 和它们的标签 $y_k$。

4. 训练更新:

   • 使用 $D_{PT}$，$D_{PL}$，和 $D_L$ 对模型 $G_{\text{epoch}?1}$，$C_{\text{epoch}?1}$ 进行训练。
   • 优化结合了公式(3)和公式(5)定义的损失函数。
   • 更新模型参数为 $G_{\text{epoch}}$ 和 $C_{\text{epoch}}$。

5. 算法结束:

   • 当达到最大训练周期 MaxEpoch 后，训练结束。

通过这种方法，模型在训练过程中不断更新，同时使用生成的伪标签和软伪文本来增强训练，这可能有助于模型在处理无标签数据时提高其性能和泛化能力。伪标签数据 $D_{PL}$ 和软伪文本数据 $D_{PT}$ 在这个过程中起到增强学习的作用，它们分别提供了伪标签和文本生成的软输出来训练模型。

理论分析

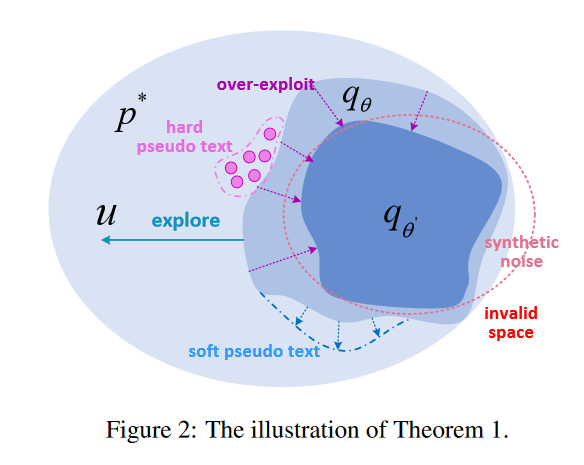
定理1. 优化DuNST的训练目标等价于近似最小化以下上界：

$$KL[p^{?}||q_{\theta }]+KL[p^{{\theta }^{\prime }}||q_{\theta }]+KL[u||q_{\theta }],\text{\hspace{1em}(6)}$$

其中 $p^{?}$ 是真实文本分布，$q_{\theta }$ 和 $q_{{\theta }^{\prime }}$ 分别是当前和上一次ST迭代时模型的估计，而 $u$ 是噪声分布。

在定理1中，第一个KL项对应于方程(3)的优化，它近似了真实分布。第二个项对应于经典的自训练，它作为一种正则化手段。如图2所示，这种正则化迫使模型拟合已经学习的空间，导致过度利用。最后一个是噪声项，用于增强探索。与各向同性合成噪声（太嘈杂）和硬伪文本（太稀疏）相比，DuNST搭配软伪文本能够探索潜在方向，更平滑地覆盖更大的空间，从而进一步推动边界。